Este documento presenta un curso sobre columnas de hormigón armado según el Código CIRSOC 201-2005. El curso cubre temas como columnas normales y zunchadas, diagramas de interacción, análisis de segundo orden, sistemas desplazables e indesplazables, y ejemplos de aplicación. El objetivo es enseñar los métodos de diseño y análisis de columnas de hormigón armado según la normativa actualizada.




![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
LEYES CONSTITUTIVAS DE LOS MATERIALES
fy
0,85 f’c
0,85 f’c
3,0(1-β1) 3,0 2,1 3,0
ε [0/00] (ADN420) ε [0/00]
HORMIGON ACERO
Donde:
β1 = 0,85 para f’c ≤ 30 Mpa
β1 = 0,85 – 0,05 (f’c – 30 MPa) / 7 ≥ 0,65 para f’c > 30 MPa
COLUMNAS DE HORMIGON ARMADO Lámina 5](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-5-320.jpg)


![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
COLUMNAS CORTAS CON ESTRIBOS NORMALES
Fórmula de adición
COMPRESION PURA
RESISTENCIA n
'
[
φP = 0.80φ 0.85fc (Ag − Ast ) + fy Ast ]
MAXIMA CON Mu = 0
Donde:
Ag : Sección bruta de hormigón
Ast: Sección total de armadura
∅ = 0,65 para combinación de cargas según art.9.2:
U= 1,4 (D + F)
U= 1,2 (D+F+T) + 1,6(L+H) + 0,5 (Lr ó S ó R)
......................
Etc.
Para cargas gravitatoria, permanentes y sobrecargas, de uso en edificios normales:
U= 1,4 D
U= 1,2 D + 1,6 L
COLUMNAS DE HORMIGON ARMADO Lámina 8](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-8-320.jpg)
![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
COLUMNAS CORTAS CON ZUNCHOS EN ESPIRAL
COMPRESION PURA Fórmula de adición
RESISTENCIA
MAXIMA CON Mu = 0
n
[
φP = 0.85φ 0.85fc (Ag − Ast) + fy Ast
'
]
Donde:
Ag : Sección bruta de hormigón
Ast: Sección total de armadura
∅ = 0,70 para combinación de cargas según art.9.2:
U= 1,4 (D + F)
U= 1,2 (D+F+T) + 1,6(L+H) + 0,5 (Lr ó S ó R)
......................
Etc.
Para cargas permanentes y sobrecargas de uso en edificios normales:
U= 1,4 D
U= 1,2 D + 1,6 L
COLUMNAS DE HORMIGON ARMADO Lámina 9](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-9-320.jpg)





![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005” Diagrama de interacción simplificado – Columnas rectangulares
[ ( )
φ.P0n = φ. 0.85.f'c . A g − A st + A st .fy ]
φ.Pn
[ ( )
φ.Pn(max) = φ ⋅ 0.80 ⋅ 0.85 ⋅ f'c . Ag − Ast + Ast ⋅ fy ]
φ.P0n φ.Pbn = φ ⋅ 0.43 ⋅ h ⋅ b.f'C
h
φ.Pn(max) φ.Mbn = φ.Pbn .0.32.h + φ.[0.6.A se + 0.15.A ss ].fy . − d'
2
φ.Ptn = φ.A stotal .fy
φ.Pbn
φ.Mn φ.Mbn
φ.Mbn Ase Ass
h
φ.Ptn
b
COLUMNAS DE HORMIGON ARMADO Lámina 15](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-15-320.jpg)






















![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
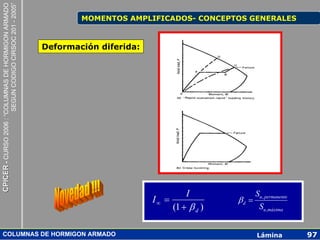
MOMENTOS AMPLIFICADOS- CONCEPTOS GENERALES
Módulo de elasticidad: E c = 4700 f c′ [MPa]
Momentos de inercia: Vigas 0.35 Ig
Columnas 0.70 Ig
Tabiques no fisurados 0.70 Ig
Para cargas de
servicio, se pueden Tabiques fisurados 0.35 Ig
utilizar estos valores
de momentos de Entrepisos sin vigas 0.25 Ig
inercia multiplicados
por 1.43 Areas 1.00 Ag
COLUMNAS DE HORMIGON ARMADO Lámina 38](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-38-320.jpg)



















![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
MOMENTOS AMPLIFICADOS - PORTICOS INDESPLAZABLES
Art. 10.11.4
A. Es evidente que el sist. o nivel es indesplazable? ó
SI B. Es MII ≤ 1.05 MI ? ó
NO
C. Es Q =
∑P∆ u 0
≤ 0.05...........conVu ≠ 0 ? [Ec. 10.7]
Vu lc
MI Momento en extremo de columna obtenido por análisis de
Sistema o nivel
primer orden.
DESPLAZABLE
Q Índice de estabilidad. Aplicar
Art. 10.13
Σ Pu Carga vertical total mayorada; sumatoria de todas las
cargas de columnas y tabiques en el nivel considerado.
∆0 Deformación horizontal relativa de primer orden,
determinada en forma elástica, debida a Vu y
correspondiente al extremo superior con respecto al
inferior del nivel considerado.
Vu Corte horizontal mayorado en el nivel considerado.
lc Altura del elemento comprimido, medida desde centro a
centro de los nudos del pórtico.
SISTEMAS O NIVELES INDESPLAZABLES
I
COLUMNAS DE HORMIGON ARMADO Lámina 58](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-58-320.jpg)

![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
II
SI
NO Hay cargas transversales en el
elemento comprimido, entre
apoyos ?
Cm = 1
Cm = 1 ó Cm= 0.6 + 0.4 M1 / M2 ≥ 0.4
[Ec.10-14]
Con /M2/ ≥ /M1/
M2 M2
M1 M1 III
Curvatura simple Curvatura doble
0≤ M1 / M2 ≤ 1 -1 ≤ M1 / M2 ≤ 0
Nota: En Ec.10-14, se debe utilizar el valor de
M2 obtenido en el análisis estructural, aún si
se aplica el valor mínimo dado por la Ec. 10-
15.
COLUMNAS DE HORMIGON ARMADO Lámina 60](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-60-320.jpg)
![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
III
Calcular: M c = δ ns . M 2 [Ec.10 -9]
con valor mínimo: M 2
≥ Pu (15 mm + 0 . 03 h ) [Ec.10.15]
Cm
δ ns = ≥1 [Ec.10 -10]
Pu
1− u
0 . 75 Pc
c
donde:
π 2 .E .I
Pc =
c [Ec.1 0-14]
( k ns .l u ) 2
Adoptando:
0 . 2 E c I g + E s . I se 0 .4 E c I g
EI = [Ec.10 -12] ó EI = [Ec.10 -13]
1+ βd 1+ βd
Pu , PERMANENTE
siendo βd = (Si se adopta β d = 0 . 6 ⇒ EI = 0 . 24 E c I g )
Pu , MAXIMA
IV
COLUMNAS DE HORMIGON ARMADO Lámina 61](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-61-320.jpg)
















![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO 10.13
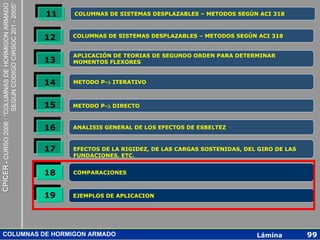
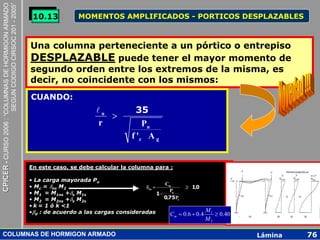
10.13 MOMENTOS AMPLIFICADOS - PORTICOS DESPLAZABLES
SEGUN CODIGO CIRSOC 201 - 2005”
DIAGRAMA DE FLUJO
Art. 10.11.4
A. Es evidente que el sist. o nivel es indesplazable? ó
NO SI
II I
B. Es M ≤ 1.05 M ? ó
C. Es Q =
∑P∆ u 0
≤ 0.05...........conVu ≠ 0 ? [Ec. 10.7]
Vulc
MI Momento en extremo de columna obtenido por análisis de Sistema o nivel
primer orden. INDESPLAZABLE
Aplicar
Q Índice de estabilidad. Art. 10.12
Σ Pu Carga vertical total mayorada; sumatoria de todas las
cargas de columnas y tabiques en el nivel considerado.
∆0 Deformación horizontal relativa de primer orden,
determinada en forma elástica, debida a Vu y
correspondiente al extremo superior con respecto al
inferior del nivel considerado.
Vu Corte horizontal mayorado en el nivel considerado.
lc Altura del elemento comprimido, medida desde centro a
centro de los nudos del pórtico.
SISTEMAS O NIVELES DESPLAZABLES III
COLUMNAS DE HORMIGON ARMADO Lámina 81](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-81-320.jpg)

![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
V
NO SI
Ks lu / r > 100 Se debe utilizar un
análisis de segundo
orden de acuerdo al
Art. 10.10.1 para
calcular las
solicitaciones en el
sistema estructural
analizado.
CALCULAR:
M1 = M1ns + δs M1s [Ec. 10-16]
M2 = M2ns + δs M2s [Ec. 10-17]
Mins : Momentos flexores debidos a cargas que no producen deformaciones
laterales apreciables.
Mis : Momentos flexores debidos a cargas que producen deformaciones
laterales apreciables.
OPCION 2 ó 3
COLUMNAS DE HORMIGON ARMADO Lámina 83](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-83-320.jpg)
![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
2 OPCION 2. METODO DIRECTO P-∆
Calcular:
Ms
δ s .M s = ≥ Ms [Ec. 10-17]
1− Q
δs ≤ 1,5
A
COLUMNAS DE HORMIGON ARMADO Lámina 84](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-84-320.jpg)
![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005” A
VERIFICAR SI EL MAXIMO MOMENTO DE SEGUNDO ORDEN SE
ENCUENTRA ENTRE LOS EXTREMOS DE LA COLUMNA:
Art. 10.13.5
SI lu 35 NO MOMENTO
MOMENTO
> MAXIMO EN
MAXIMO r Pu EXTREMO DE
COLUMNA
ENTRE
EXTREMOS DE f 'c . Ag
LA COLUMNA
[Ec. 10-19]
3b.
2c Dimensionar
2a armadura con M1 , M2
y Nu
COLUMNAS DE HORMIGON ARMADO Lámina 85](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-85-320.jpg)
![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
2a MOMENTO MAXIMO ENTRE EXTREMOS DE LA COLUMNA
Calcular de acuerdo al Art. 10.12.3:
M c , 2 = δ ns .M 2 [Ec.10-9]
M 2 = M 2 ns + δ s .M 2 s
M2 calculado de acuerdo al Art. 10.13.3 [Ec.10-16 y 10-17]
con valor mínimo: M 2 ≥ Pu (15mm+ 0.03h) [Ec.10.15]
Cm
δ ns = ≥1 M1 [Ec.10-10]
Pu Cm = 0.6 + 0.4 ≥ 0.40
1− M2
0.75Pc
(Si δns < 1, el momento máximo se encuentra en uno de los extremos)
π 2 .E.I
Pc = 2
[Ec.10-11]
(kns .lu )
Adoptando:
0.2 E c I g + Es .I se 0.4Ec I g
EI =− [Ec.10-12] ó EI = [Ec.10-13]
1+ βd 1+ βd
♦Calcular la armadura con el valor del esfuerzo axil Pu y el
momento Mc. 2c
COLUMNAS DE HORMIGON ARMADO Lámina 86](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-86-320.jpg)


![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
3 OPCION 3. FACTOR DE AMPLIFICACION
Calcular:
Ms
δ s .M s = ≥ Ms [Ec. 10-18]
1−
∑ PU
0.75∑ PC
B
COLUMNAS DE HORMIGON ARMADO Lámina 89](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-89-320.jpg)

![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005” B
VERIFICAR SI EL MAXIMO MOMENTO DE SEGUNDO ORDEN SE
ENCUENTRA ENTRE LOS EXTREMOS DE LA COLUMNA:
Art. 10.13.5
SI lu 35 NO MOMENTO
MOMENTO
> MAXIMO EN
MAXIMO r Pu EXTREMO DE
COLUMNA
ENTRE
EXTREMOS DE f 'c . Ag
LA COLUMNA
[Ec. 10-19]
3b.
3c Dimensionar
3a armadura con M1 , M2
y Nu
COLUMNAS DE HORMIGON ARMADO Lámina 91](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-91-320.jpg)
![CPICER - CURSO 2006 : “COLUMNAS DE HORMIGON ARMADO
SEGUN CODIGO CIRSOC 201 - 2005”
3a MOMENTO MAXIMO ENTRE EXTREMOS DE LA COLUMNA
Calcular de acuerdo al Art. 10.12.3:
M c , 2 = δ ns .M 2 [Ec.10-9]
M 2 = M 2 ns + δ s .M 2 s
M2 calculado de acuerdo al Art. 10.13.3 [Ec.10-16 y 10-17]
con valor mínimo: M 2 ≥ Pu (15mm+ 0.03h) [Ec.10.15]
Cm
δ ns = ≥1 M1 [Ec.10-10]
Pu Cm = 0.6 + 0.4 ≥ 0.40
1− M2
0.75Pc
(Si δns < 1, el momento máximo se encuentra en uno de los extremos)
π 2 .E.I
Pc = 2
[Ec.10-11]
(kns .lu )
Adoptando:
0.2 E c I g + Es .I se 0.4Ec I g
EI =− [Ec.10-12] ó EI = [Ec.10-13]
1+ βd 1+ βd
♦Calcular la armadura con el valor del esfuerzo axil Pu y el
momento Mc. 3c
COLUMNAS DE HORMIGON ARMADO Lámina 92](https://image.slidesharecdn.com/columnasdeconcretoarmado-130206152206-phpapp02/85/Columnas-de-concreto-armado-92-320.jpg)