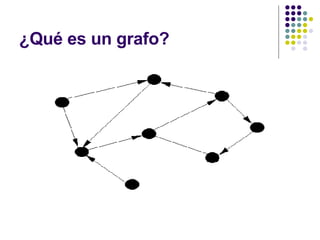
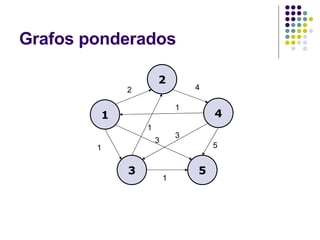
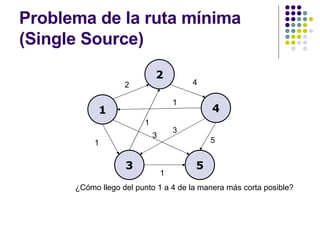
El documento explica los conceptos básicos de grafos y el problema de encontrar el camino más corto entre dos vértices en un grafo. Describe el algoritmo de Dijkstra para resolver este problema de manera eficiente en un grafo ponderado. También presenta variaciones como encontrar los caminos más cortos desde múltiples fuentes y su aplicación para problemas de logística como determinar el centro de distribución óptimo.

1. Caminos más cortos a partir de múltiples fuentes en un grafo Joemmanuel Ponce Galindo

2. ¿Qué es un grafo?

3. Un grafo es… Una pareja ordenada G(V,E) con las siguientes características: V es un conjunto de vértices E es un conjunto de parejas de distintos vértices, entre los cuales se trazan líneas (aristas)

4. Grafos ponderados 1 2 4 3 5 2 4 1 1 5 3 1 1 3

5. Entonces l(a) = peso de la arista ‘a’ l(x,y) = peso de la arista de x a y

6. ¿Y qué podemos modelar? 1 0 3 5 6 4 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 5 3 8 6 1 2 4 3 5 1 1 1 1 1 2 4 2 3 3 2 1 3

7. Problema de la ruta mínima (Single Source) ¿Cómo llego del punto 1 a 4 de la manera más corta posible? 1 2 4 3 5 2 4 1 1 5 3 1 1 3

8. ¿Cómo se resuelve? Existen algoritmos genéricos para ello: Dijkstra Algorithm Floyd Algorithm Bellman-Ford Algorithm

9. Algoritmo de Dijkstra Algoritmo glotón (greedy) Punto de inicio s Conjunto S Vector D 1 2 4 3 5 2 4 1 1 5 3 1 1 3

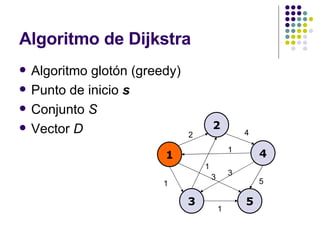
10. Condiciones iniciales S={ 1 } V-S={ 2,3,4,5 } D=[ 0 , 2,1, ∞,3 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

11. El algoritmo Aumentar S agregando el elemento v en V-S tal que D v sea el mínimo de ese conjunto. Actualizar los valores de D i para todos los elementos i existentes en V-S . D i =mínimo( D i , D v +f(v, i) ) Terminar cuando |S|=|V|

12. Paso a paso (Iteración 1) Buscar mínimo D i en V-S S={ 1 } V-S={ 2,3,4,5 } D=[ 0 , 2,1, ∞,3 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

13. Paso a paso (Iteración 1) Agregar elemento a S . Actualizar D S={ 1,3 } V-S={ 2,4,5 } D=[ 0 , 2 , 1 , ∞,3 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

14. Paso a paso (Iteración 2) Buscar mínimo D i en V-S S={ 1,3 } V-S={ 2,4,5 } D=[ 0 , 2 , 1 , ∞,2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

15. Paso a paso (Iteración 2) Agregar elemento a S . Actualizar D S={ 1,3,2 } V-S={ 4,5 } D=[ 0 , 2 , 1 , ∞ , 2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

16. Paso a paso (Iteración 3) Buscar mínimo D i en V-S S={ 1,3,2 } V-S={ 4,5 } D=[ 0 , 2 , 1 , 6 , 2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

17. Paso a paso (Iteración 3) Agregar elemento a S . Actualizar D S={ 1,3,2,5 } V-S={ 4 } D=[ 0 , 2 , 1 , 6 , 2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

18. Paso a paso (Iteración 4) Buscar mínimo D i en V-S S={ 1,3,2,5 } V-S={ 4 } D=[ 0 , 2 , 1 , 6 , 2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

19. Paso a paso (Iteración 4) Agregar elemento a S . Actualizar D S={ 1,3,2,5,4 } V-S={ } D=[ 0 , 2 , 1 , 6 , 2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

20. Final |S| = |V| La mejor manera de llegar al vértice u se encuentra en D u S={ 1,3,2,5,4 } V-S={ } D=[ 0 , 2 , 1 , 6 , 2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

21. ¿Por qué funciona? Supongamos delta(s,v) = Mejor manera de llegar de s a v Si Dijkstra funciona: D u = delta(s,u) para toda u en V

22. Demostración por contradicción Suponga que u es el primer vértice añadido a S tal que D u ≠ delta(s,u)

23. Propiedades que tendría u u no puede ser s porque D s = 0 Existe un camino de s a u , de lo contrario D s = ∞ Si existe un camino, entonces debe existir el camino más corto.

24. Suposición principal Sea s->(p1)->x->y->(p2)->u el camino más corto de s a u .

25. Propiedades de x y y x ya fue insertado en S D x =delta(s,x) Posteriormente se actualizó el vértice y , así que D y =delta(s,y) , pero aun no es insertado en S

26. Entonces Puesto que y se encuentra antes que u: D y =delta(s,y) ≤ D u ≤ delta(s,u) Pero partimos de que u esta siendo insertado en S , así que se debe cumplir que: D y ≥ D u

27. Finalmente Así que: D y =delta(s,y) = D u =delta(s,u)

28. El Multiple Source Shortest-Path Problem 1 2 4 3 5 2 4 1 1 5 3 1 1 3

29. ¿Cuál es el problema? ¿Cuál es la mejor manera de llegar al los puntos T (town o ciudad en naranja) a partir de cualquiera de los puntos S (fuente) ?

30. Consideraciones Existe un conjunto de fuentes F En el camino más corto para llegar a u , existe sólo una fuente: f 1 ->(p1)-> f 2 ->(p2)->v > f 2 ->(p2)->v

31. Un problema más real Puntos Naranjas: Centros de Distribución Puntos Grises: Ciudades ¿De qué centro de distribución es mejor partir a la ciudad X de tal manera de que gaste los menos recursos posibles? 5 1 2 4 3 5 2 4 1 1 3 1 1 3

32. ¿Qué otro problema podemos resolver? Puntos Naranjas: Centros de Distribución Puntos Grises: Ciudades Quiero construir un nuevo Punto de Distribución ¿Cuál es el mejor lugar para hacerlo? 1 2 4 3 5 2 4 1 1 3 1 1 3

33. ¿Cómo lo resolvemos con Dijkstra? Algoritmo glotón (greedy) Puntos de inicio Conjunto F Conjunto S Vector D

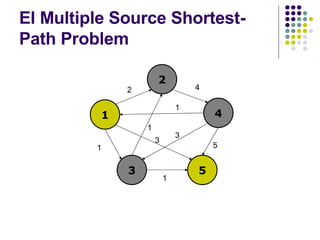
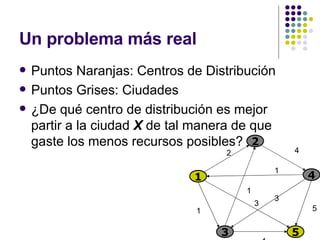
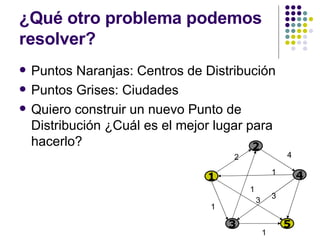
34. Condiciones iniciales S= F ={ 1,2 } V-S={ 3,4,5 } D=[ 0 , 0 ,1, 4,3 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

35. Estado final S={ 1,5,4,3,2 } V-S={} D=[ 0 , 0,1, 4,2 ] 1 2 3 4 5 1 2 4 3 5 2 4 1 1 5 3 1 1 3

36. Conclusiones Complejidad O(v 2 ) pudiéndose reducir a O(nlogn) con Busqueda Binaria Procesa hasta 10,000 vértices en 1 segundo El Algoritmo de Dijkstra es rápido Demostramos que resuelve eficazmente nuestro problema