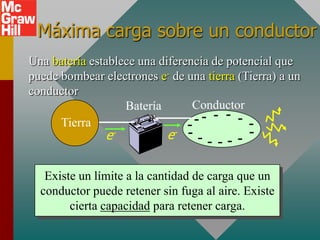
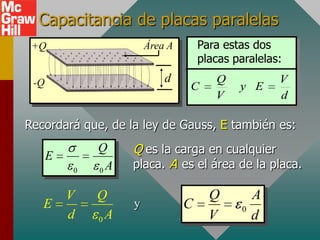
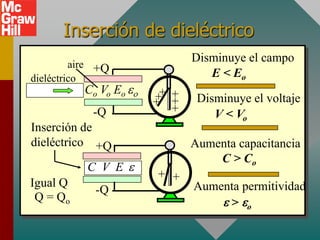
Este documento presenta conceptos clave sobre capacitancia, incluyendo: 1) la definición de capacitancia como la relación entre la carga y el voltaje en un conductor; 2) cómo la capacitancia depende de parámetros como el área, separación y constante dieléctrica; y 3) fórmulas para calcular la capacitancia, carga, voltaje y energía almacenada en capacitores.