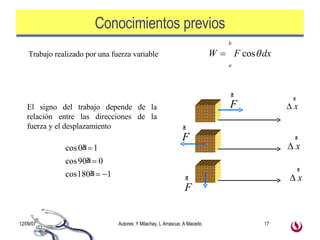
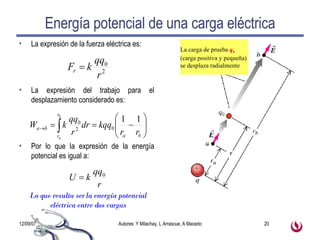
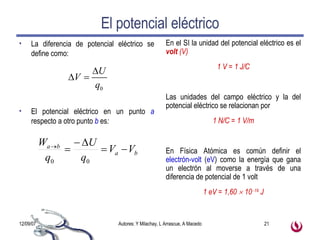
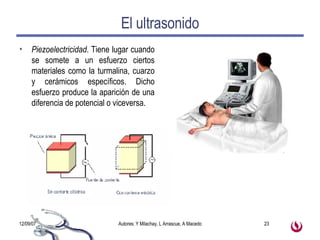
1) La carga eléctrica es una propiedad fundamental de la materia que existe en dos formas: positiva y negativa. 2) Las cargas del mismo signo se repelen y las de signo opuesto se atraen debido a la fuerza eléctrica descrita por la ley de Coulomb. 3) El campo eléctrico describe la fuerza que experimentaría una carga puntual en diferentes puntos del espacio y depende de la distribución de cargas presentes.

1. Fuerza eléctrica y Campo eléctrico Y Milachay, L Arrascue, A Macedo

2. Experimento de electrización de los cuerpos

3. La carga eléctrica La carga eléctrica, como la masa, es una propiedad fundamental de la materia. Existen dos tipos de carga eléctrica: positiva y negativa: protones y electrones Las cargas eléctricas del mismo signo se repelen y las cargas eléctricas de signos contrarios se atraen. La carga está cuantizada. Es decir, todas las cargas son un múltiplo de la carga fundamental e . Q = + ne Donde n es un número entero positivo Las características y propiedades de los átomos y moléculas se deben a las interacciones eléctricas entre las partículas que los componen. F F F F F F

4. Propiedades de la carga eléctrica La unidad de carga en el sistema internacional de unidades es el coulomb y su símbolo es C . Los valores típicos de carga se expresan utilizando algunos prefijos del sistema internacional. Prefijo micro (  = 10 – 6 )  1  C = 10 – 6 C Prefijo nano (  = 10 – 9 )  1  C = 10 – 9 C Prefijo pico ( p = 10 – 12 )  1 pC = 10 – 12 C Propiedades de las partículas con carga eléctrica e = 1,60217733 x 10 – 19 C Donde e es la carga fundamental y su valor es: Neutrón Protón Electrón cero 1,6749286 x 10 - 27 kg + e 1,6726231 x 10 - 27 kg e 9,1093897 x 10 - 31 kg Carga unitaria Masa

5. Cuando el cuerpo está cargado eléctricamente Un cuerpo es eléctricamente neutro si el número de electrones es igual al número de protones, la suma de todas las cargas es nula. Un átomo, inicialmente neutro, que pierde uno o más de sus electrones quedará cargado positivamente y se le llamará ión positivo. Un átomo inicialmente neutro que gana uno o más electrones quedará cargado negativamente y se le llamará ión negativo. Carga elemental negativa Carga elemental positiva Cuerpo con carga nula # cargas negativas=# cargas positivas Cuerpo cargado positivamente # cargas negativas<# cargas positivas Cuerpo cargado negativamente # cargas negativas># cargas positivas

6. Ejercicio de aplicación Se produce un rayo cuando hay un flujo de carga eléctrica (principalmente electrones) entre el suelo y un nubarrón. La proporción máxima de un flujo de carga al caer un rayo es de alrededor de 20 000 C/s ; esto dura 100  s más o menos. ¿Cuánta carga fluye entre el suelo y la nube en este tiempo? ¿Cuántos electrones fluyen durante este tiempo? 1  s = 10 -6 s e - = 1,60217733 x 10 – 19 C Solución : a) La cantidad de carga que fluye es igual a la tasa de descarga x tiempo de descarga. 20 000 C/s x 100 10 -6 s 2 C b)¿Cuántos electrones se han desplazado? Dividimos el resultado anterior entre la carga del electrón. 2 C/ 1,602 x 10 -19 C El resultado da: 1,25 x 10 19 electrones Cada día en el mundo se producen 8 000 000 de rayos http://www.pararrayos.info/pdf/Pararrayos%20CTS%20%20Agosto%202006.pdf

7. Blindaje eléctrico: al interior de un conductor el campo eléctrico es nulo El blindaje eléctrico es la aplicación del conocimiento del comportamiento de las cargas eléctricas. Es usado para protegerse en la reparación de líneas de alta tensión. http:// www.schwab -kolb.com/dc000096. htm Persona que ha sufrido la descarga eléctrica de un rayo

8. Ejercicio de aplicación Explique, usando conceptos de electrostática, cómo se ha podido iniciar el fuego en el surtidor de la gasolinera. Regla para proteger las tarjetas electrónicas de la electricidad estática: “ Al manejar componentes electrónicos, lleve siempre una correa de protección contra descargas electrostáticas en la muñeca o el tobillo. Conecte un extremo de la correa a un conector anti-electrostático a una pieza de metal sin pintar del sistema (como un tornillo).” ¿Por qué se debe conectar la correa a la ventana? http://www.cdc.gov/spanish/niosh/docs/98-111sp.html http://www.youtube.com/watch?v=b3x-8tj49ac

9. Ley de Coulomb Coulomb encontró que para dos cargas puntuales q 1 y q 2 (cargas de dimensiones muy pequeñas en comparación con la distancia r entre ellas), el módulo de la fuerza eléctrica es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas. http://es.wikipedia.org/wiki/Ley_de_Coulomb

10. K – constante eléctrica La constante eléctrica también se expresa como: Donde  se denomina permisividad del medio y  ´ se denomina constante dieléctrica del medio. http://amasci.com/miscon/elect.html 2,64·10 9 3,01·10 -11 Vidrio orgánico 2,25·10 9 3,54·10 -11 C-irbolito 2,04·10 9 3,90·10 -11 Baquelita 8,56·10 9 9,30·10 -12 Poliestireno 4,09·10 9 1,95·10 -11 Papel parafinado 1,38·10 9 5,76·10 -11 Mica 4,16·10 9 1,90·10 -11 Parafina 8,99·10 9 8,85·10 -12 Vacío k  ´  Material

11. Ejercicio de aplicación En una molécula de NaCl, un ión Na + con carga “e” está a 2,3 x10 -10 m del ión Cl - con carga “-e” ¿Cuánto vale la fuerza entre ambos? Solución: Una membrana celular de 1,0 x 10 -8 m de espesor tiene iones positivos a un lado y iones negativos al otro. ¿Cuál es la fuerza entre estos dos iones de carga +e y –e a esta distancia? Solución:

12. Definición del campo eléctrico Definimos el campo eléctrico E en un punto como la fuerza eléctrica F experimentada por una carga de prueba q o en el punto, dividida entre la carga q o . De esta manera podemos caracterizar el espacio con esa magnitud y determinar la fuerza que actuaría sobre cualquier carga ubicada en dicha posición. + +

13. Campo eléctrico de cargas puntuales Por la ley de Coulomb: Definición de campo eléctrico: Reemplazando (1) en (2):

14. Ejercicio de aplicación Un virus del mosaico del tabaco tiene una longitud de 3 000 Å y cargas de +e y −e en sus extremos. Dibuje la distribución espacial del campo eléctrico.

15. Ejercicio de aplicación Dos cargas de 6,00 nC y 3,00 nC están ubicadas en los vértices del rectángulo mostrado. ¿Cuál es el valor del campo eléctrico en el vértice A? Solución: Solución q 2 =3,00 nC q 1 =6,00 nC A 0,200 m 0,600 m

16. Otra forma de ver de los peces http:// sunsite.dcc.uchile.cl /nuevo/ciencia/ CienciaAlDia /volumen3/numero1/ articulos /articulo1. html Gymnotus carapo Gnatonemus petersii

17. Conocimientos previos Trabajo realizado por una fuerza variable El signo del trabajo depende de la relación entre las direcciones de la fuerza y el desplazamiento

18. Energía potencial eléctrica. Potencial eléctrico

19. Energía potencial mecánica El trabajo de una fuerza F que se aplica sobre un cuerpo que se desplaza de a a b es igual a: Si la fuerza es conservativa, siempre se puede expresar el trabajo como la diferencia de las energías potenciales inicial y final . Un caso típico es la energía potencial gravitacional relacionada con el trabajo del peso de un cuerpo.

20. Energía potencial de una carga eléctrica La expresión de la fuerza eléctrica es: La expresión del trabajo para el desplazamiento considerado es: Por lo que la expresión de la energía potencial es igual a: Lo que resulta ser la energía potencial eléctrica entre dos cargas La carga de prueba q 0 (carga positiva y pequeña) se desplaza radialmente

21. El potencial eléctrico La diferencia de potencial eléctrico se define como: El potencial eléctrico en un punto a respecto a otro punto b es : En el SI la unidad del potencial eléctrico es el volt (V) 1 V = 1 J/C Las unidades del campo eléctrico y la del potencial eléctrico se relacionan por 1 N/C = 1 V/m En Física Atómica es común definir el electrón-volt ( eV ) como la energía que gana un electrón al moverse a través de una diferencia de potencial de 1 volt 1 eV = 1,60  10  19 J

22. Campo eléctrico entre placas paralelas Una batería de V volts se conecta entre dos placas paralelas. La separación entre las placas es d metros y el campo eléctrico se supone uniforme. ¿Cuál es el campo eléctrico E entre las placas en función de V y d . Solución El trabajo que requiere realizar el campo para desplazar una carga desde un extremo al otro de las placas es igual a la fuerza por la distancia. Como la fuerza eléctrica es constante (campo uniforme): E =  V / d

23. El ultrasonido Piezoelectricidad . Tiene lugar cuando se somete a un esfuerzo ciertos materiales como la turmalina, cuarzo y cerámicos específicos. Dicho esfuerzo produce la aparición de una diferencia de potencial o viceversa.

24. Ejercicio de aplicación Cuál es la magnitud del campo eléctrico a través de la membrana de un axón de 1,0 x10 -8 m de espesor, si el potencial de reposo es de -70 mV . Solución:

25. Ejercicio de aplicación Una partícula con una carga de +4,20 nC está inicialmente en reposo en un campo eléctrico uniforme E dirigido hacia la izquierda. Al quedar en libertad, la partícula se desplaza a la izquierda y, después de recorrer 6,00 cm , su energía cinética resulta ser de 1,50 x 10 -6 J . a) ¿Qué trabajo realizó la fuerza eléctrica? b) ¿Cuál es la diferencia de potencial entre los puntos de partida y llegada? c) ¿Cuál es la magnitud de E ? Solución q = +4,20 nC v 0 =0 m/s d = 6,00 cm E kf = 1,50 x 10 -6 J E 6,00 cm a b (a) (b) q (c)

26. Ejercicio de aplicación Una membrana semipermeable es permeable al ión de nitrato NO 3 - , pero impermeable a los iones de plata, Ag + . Dos soluciones de nitrato de plata, con diferentes concentraciones, se aplican a un lado de la membrana. Describa y explique el origen del campo eléctrico en la membrana cuando se ha alcanzado el equilibrio.

27. Ejercicio de aplicación La membrana celular tiene una densidad de carga de -1,5 x10 -6 C/m 2 en su superficie externa. Dibuje el campo eléctrico entre las capas de la célula. Si la constante dieléctrica de la célula es 8,0 , calcule el campo eléctrico entre las capas exterior e interior de la célula. Si el espesor de la membrana es de 0,75  m , calcule la diferencia de potencial entre las capas de la membrana.

28. Ejercicio de aplicación Un electrón es acelerado entre dos electrodos separados 40 mm en un tubo de rayos x que funciona a una diferencia de potencial de 20 kV . Calcule la fuerza promedio que actúa sobre el electrón. Calcule la energía cinética del electrón justo antes de que impacte sobre el electrodo positivo.