Este documento describe los principios fundamentales de la mecánica cuántica, incluyendo la cuantización del momento magnético atómico demostrado por el experimento de Stern-Gerlach, la descripción matemática de los estados cuánticos mediante espacios de Hilbert y la evolución unitaria, y las diferencias clave entre bits clásicos y qubits cuánticos que permiten la superposición y el entrelazamiento.

1. 1
´ ´
Computacion y criptograf´a cuanticas
ı
´
DAVID C EREZO S A NCHEZ
http://david.cerezo.name

2. 2
Requisitos
´
Teor´a de la Recursion
ı
Complejidad Computacional
Criptograf´a
ı
´
Algebra lineal
´ ´
Mecanica cuantica

3. 3
´ ´
Los postulados de la Mecanica Cuantica
1. Asociado a cualquier sistema f´sico aislado hay un espacio vectorial complejo, infinita-
ı
mente dimensional, con producto interno y completo, esto es, un espacio de Hilbert,
conocido como el espacio de estados del sistema. El sistema viene completamente
descrito por su vector de estado, que es un vector unitario en el espacio de estados del
sistema.
2. ´ ´ ´
La evolucion de un sistema cuantico cerrado es descrita por una transformacion unitaria:
el estado |ψ del sistema en un instante de tiempo t1 se relaciona con el estado |ψ del
sistema en un instante de tiempo t2 por el operador unitario U que depende solo de los
´
instantes t1 y t2 ,
|ψ = U |ψ . (1)
a) ´ ´
La evolucion temporal de los estados de un sistema cuantico cerrado viene descrita
´ ¨
por la ecuacion de Schrodinger,
d |ψ
i = H |ψ , (2)
dt

4. 4
donde es la constante de Planck y H es la Hamiltonian del sistema cerrado. La
´ ´
relacion entre 1 y 2 sera
−iH (t2 − t1)
|ψ (t2) = exp |ψ (t1) = U (t1,t2) |ψ (t1)
con U siendo el operador unitario, existiendo una correspondencia entre la descripcion
´
en tiempo discreto con operadores unitarios y la de tiempo continuo usando Hamilto-
nians.
3. Las mediciones cuanticas vienen descritas por un conjunto {Mm } de operadores de me-
´
dida, actuando en el espacio de estados del sistema que miden. Si el estado del sistema
es |ψ antes de la medida entonces la probabilidad de que el resultado m ocurra viene
dada por
P (m) = ψ| MmMm |ψ ,
†
´ ´ ´
y el estado del sistema despues de la medicion sera
Mm |ψ
.
ψ| MmMm |ψ
†

5. 5
´
Los operadores de medida deben satisfacer la ecuacion de completitud,
∑ MmMm = I.
†
m
a) El principio de incertidumbre de Heisenberg(1927),
1
x p≥
2
donde x es la incertidumbre en la posicion y
´ p es la incertidumbre en el momento,
y,
1
E t≥
2
donde E es la incertidumbre en la energ´a y
ı t es la incertidumbre en el tiempo.
4. El espacio de estados de un sistema f´sico compuesto es el producto tensorial del espacio
ı
de estados de los sistemas f´sicos componentes. Con sistemas 1 . . . n y el estando el
ı
sistema i preparado en el estado |ψi , el estado de todo el sistema es |ψ1 ⊗ |ψ2 ⊗ · · · ⊗
|ψn .

6. 6
a) Principio de superposicion de la mecanica cuantica: si |x e |y son dos estados de
´ ´ ´
un sistema cuantico, cualquier superposicion α |x + β |y deber´a ser un estado del
´ ´ ı
2 2
sistema cuantico siempre y cuando cumpla |α| + |β| = 1.
´
b) Entanglement: el estado de sistema compuesto que tiene la propiedad de no poder
ser descrito como el producto de estados de sus sistemas componentes. Por ejemplo,
√
en el estado con dos qubits |ψ = (|00 + |11 ) / 2 no existen dos estados qubit
|a y |b tales que |ψ = |a |b .

7. 7
Bits vs. Qubits
´ ´
En un ordenador clasico, los bits toman los valores 0 y 1; en un ordenador cuantico, los
qubits toman los valores α |0 + β |1 , con α, β ∈ C.
´
Cuando se realizan mediciones de los valores en un ordenador clasico, obtenemos como
2
resultado 0 o 1; en un ordenador cuantico, obtenemos |0 con probabilidad |α| o |1 con
´ ´
2
probabilidad |β| .
´
En el ordenador clasico, las operaciones elementales son
0→0 0→1
1→0 1→1
´
en el ordenador cuantico realizan rotaciones en el plano,
Esfera de Bloch

8. 8
θ θ
|ψ = α |0 + β |1 = cos |0 + eiϕ sin |1
2 2
Vector de Bloch: (cos ϕ sin θ, sin ϕ sin θ, cos θ)
En un ordenador clasico con registros de l bits, solo se podr´a almacenar uno de los
´ ´ ı
2l posibles numeros, operando en un solo numero en un instante de tiempo; en un or-
´ ´ ´
denador cuantico con l qubits, se puede almacenar una superposicion de todos los 2l
´ ´
numeros y operar en los 2l numeros al mismo tiempo.
´ ´

9. 9
El experimento Stern-Gerlach
Concebido por Stern en 1921 y ejecutado por Gerlach en 1922, una de las
primeras evidencias de la existencia de qubits.
´ ´
Un rayo de atomos de plata desde un horno pasa por un campo magnetico,
´ ´ ´
desviandose y dejando constancia de la posicion de cada atomo. En 1927
´ ´
se repite con atomos de hidrogeno, para evitar los efectos derivados de
´
la complicada estructura de los atomos de plata sobre el resultado de los
experimentos.
´ ´
Los atomos seran desviados segun una cantidad dependiente del compo-
´
nente z del momento dipolar magnetico del atomo.
´ ´
´
Se esperaba que los atomos que salen del dispositivos Stern-Gerlach sigu-
´ ´ ´
iesen una distribucion continua en cuanto a la distribucion de los angu-

10. 10
´
los, ya que los atomos que salen del horno tendr´an sus dipolos orienta-
ı
´
dos aleatoriamente en cualquier direccion. Sin embargo, siguen una dis-
´
tribucion segun un conjunto de valores discretos, es decir, el momento
´
´ ´ ´
magnetico dipolar de los atomos esta cuantizado.
´ ´
En el caso del hidrogeno, se usaron aquellos atomos que tuviesen momen-
´ ´ ´
to magnetico dipolar cero, esperandose un unico rayo de atomos saliendo
´
del aparato que no se habr´a desviado. Pero en realidad se vieron dos
ı
unicos rayos.
´
´
A partir de aquel momento, el electron tendr´a asociado una nueva can-
ı
tidad f´sica conocida como spin.
ı

11. 11

12. 12

13. 13
´
V´deo: simulacion experimento
ı
Stern-Gerlach

14. 14
V´deo: experimento Stern-Gerlach
ı
´
esquematica

15. 15
V´deo: experimento Stern-Gerlach en
ı
electrones

16. 16
´
Operaciones y circuitos cuanticos
´ ´
El modelo de computacion de los circuitos cuanticos es de [Deutsch1989], y
´
fue posteriormente desarrollado por [Yao1993], en el que tambien se
´ ´
demostraba que el modelo de computacion de los circuitos cuanticos es
´ ´ ´
equivalente al modelo de la maquina de Turing cuantica, introducida en
´
[Ben1980], extendida en [Deutsch1985] y [Yao1993], con la version moderna
dada en [BV1997].
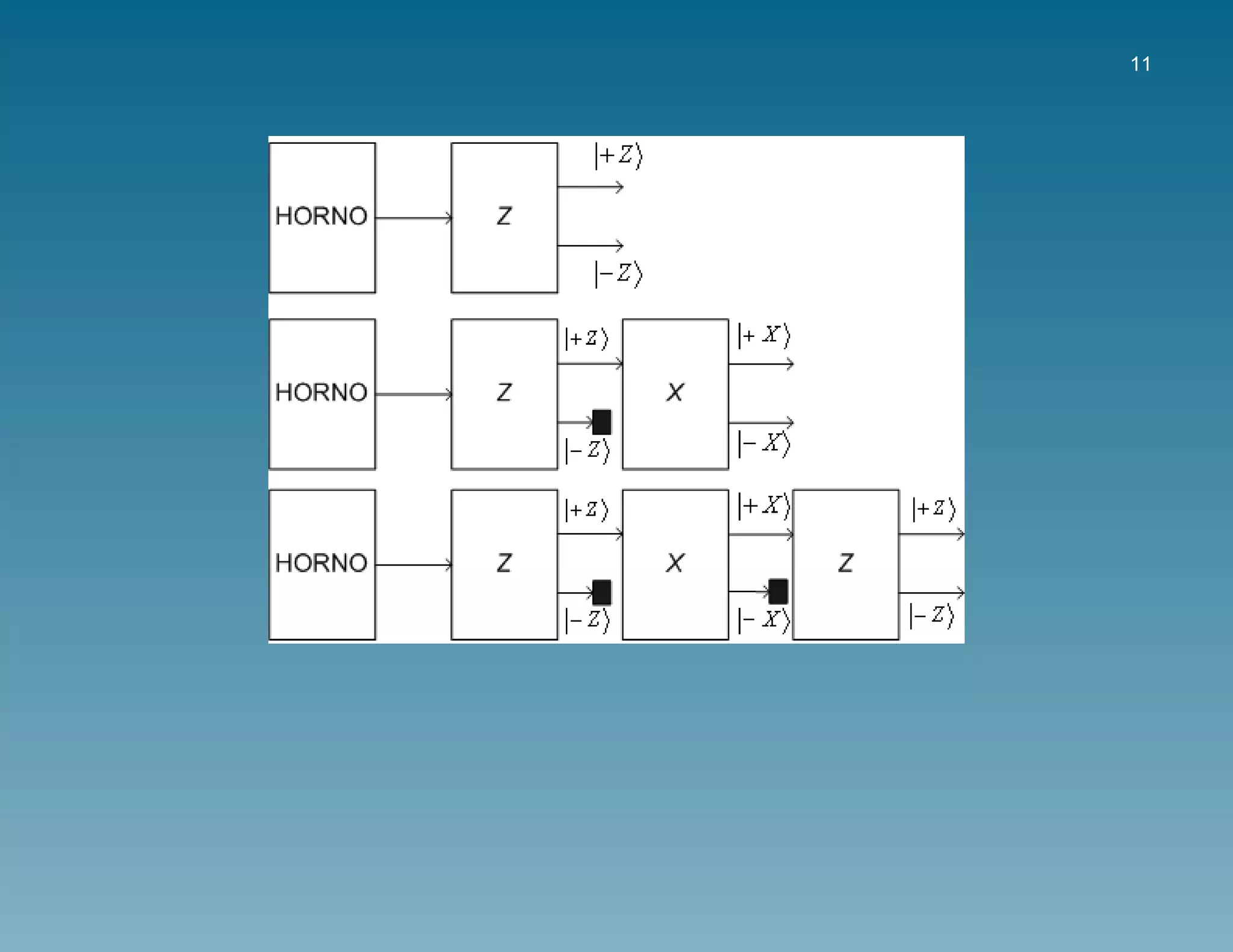
Algunas de las operaciones sobre qubits que preservan la norma son:
las matrices de Pauli
0 1 0 −i 1 0
X≡ ; Y≡ ; Z≡ ;
1 0 i 0 0 −1
donde X es la puerta cuantica NOT , Z solo cambia el signo de |1 .
´ ´

17. 17
la puerta de Hadamard
1 1 1
H=√
2 1 −1
la puerta de fase
1 0
S≡ ;
0 i
la puerta π/8
1 0
T≡
0 exp iπ
4
´ ´
Los operadores de rotacion surgen de la exponenciacion de las matrices de
Pauli:
−iθX/2 θ θ cos θ −i sin θ
Rx (θ) ≡ e = cos I − i sin X = 2 2
2 2 −i sin θ
2
θ
cos 2

18. 18
−iθY /2 θ θ cos θ − sin θ
Ry (θ) ≡ e = cos I − i sin Y = 2
θ θ
2
2 2 sin 2 cos 2
−iθZ/2 θ θ e−iθ/2 0
Rz (θ) ≡ e = cos I − i sin Z =
2 2 0 eiθ/2
Theorem 1. ´
(Descomposicion Z-Y para un unico qubit). Dada una
´
operacion unitaria U sobre un unico qubit, esta puede ser descompuesta en
´ ´ ´
U = eiαRz (β) Ry (γ) Rz (δ) , (α, β, γ, δ ∈ R) .
Corollary 1. Dada una puerta unitaria U sobre un unico qubit, existen
´
operadores unitarios A, B,C sobre un unico qubit tales que ABC = I y U =
´
eiαAXBXC, donde α es un factor de fase.
´
Operaciones mas complejas, sobre varios qubits y todas ellas reversibles,
son:

19. 19
Controlled-NOT o CNOT , con un qubit de control y otro objetivo:
 
1 0 0 0
 0 1 0 0 
CNOT = 
 0

0 0 1 
0 0 1 0
realizando la operacion |c,t
´ → |c,t ⊕ c , o mas concretamente,
´
|00 → |00 |10 → |11
.
|01 → |01 |11 → |10
Controlled-U , generalizacion del CNOT , donde U es una operacion uni-
´ ´
taria cualquiera, es decir, |c |t → |c U c |t .

20. 20
Puerta de Toffoli[Toffoli1980], generalizacion de Controlled-U .
´
Usando Hadamard, puerta de fase, controlled-NOT y puertas π/8.

21. 21
Operacion Cn (U), es una generalizacion de la puerta de Toffoli C2 (U),
´ ´
con n + k qubits y U siendo un operador unitario de k qubits:
Cn (U) |x1x2 . . . xn |ψ = |x1x2 . . . xn U x1x2...xn |ψ .
Theorem 2. ´
(Universabilidad en puertas cuanticas)[DiVincenzo1995].
Cualquier puerta logica de multiples qubits puede ser compuesta con CNOT y
´ ´

22. 22
´
por puertas de un unico qubit, o lo que es lo mismo, que cualquier operacion
´
sobre n qubits puede ser implementada componiendo puertas sobre qubits
unicos y CNOTs.
´
´ ´ ´
Ademas, tambien se puede conseguir la universabilidad tambien se puede
conseguir utilizando el conjunto discreto formado por la puerta de
Hadamard, de fase, CNOT y π/8[BMPRV1999], e intercambiando π/8 por la
puerta de Toffoli.
´
Tambien hay que tener en cuenta que no todas las operaciones unitarias
pueden ser implementadas eficientemente: hay algunas sobre n qubits que
requieren de Ω (2n log (1/ε) / log (n)) puertas para aproximarse dentro de
una distancia εusando cualquier conjunto finito de puertas[Knill1995].
Todav´a no se sabe que clase de familias de operaciones unitarias pueden
ı
´
ser computadas eficientemente en el modelo de los circuitos cuanticos.
Los errores causados por una secuencia de puertas es de como mucho la
suma de los errores de las puertas individuales[BV1997].
´ ´
Mas sobre circuitos cuanticos se puede encontrar en [BBCAl1995, Div1998].

23. 23
´
Un circuito cuantico sencillo podr´a ser el que intercambia los estados de dos
ı
qubits:
|a, b → |a, a ⊕ b
→ |a ⊕ (a ⊕ b) , a ⊕ b = |b, a ⊕ b
→ |b, (a ⊕ b) ⊕ b = |b, a
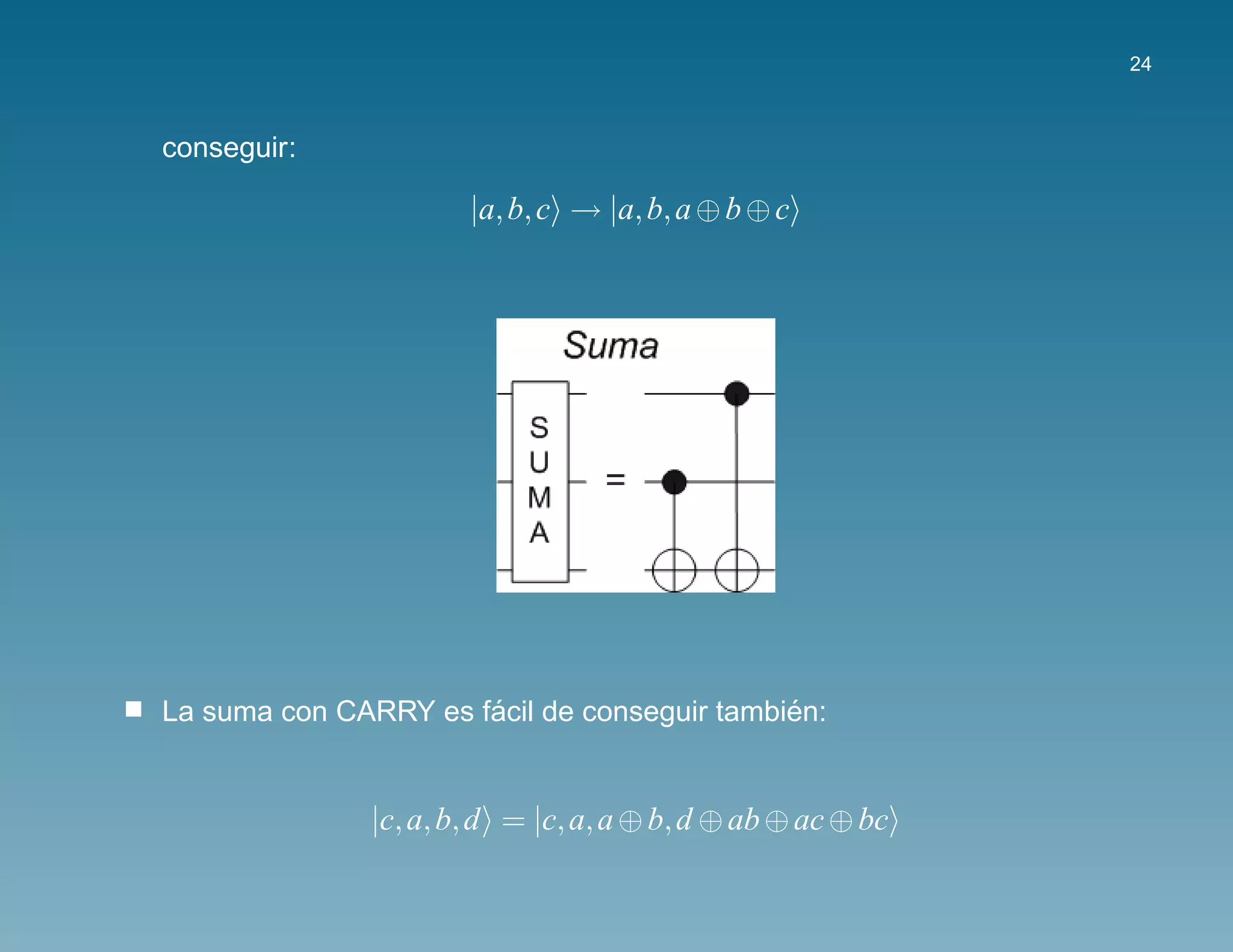
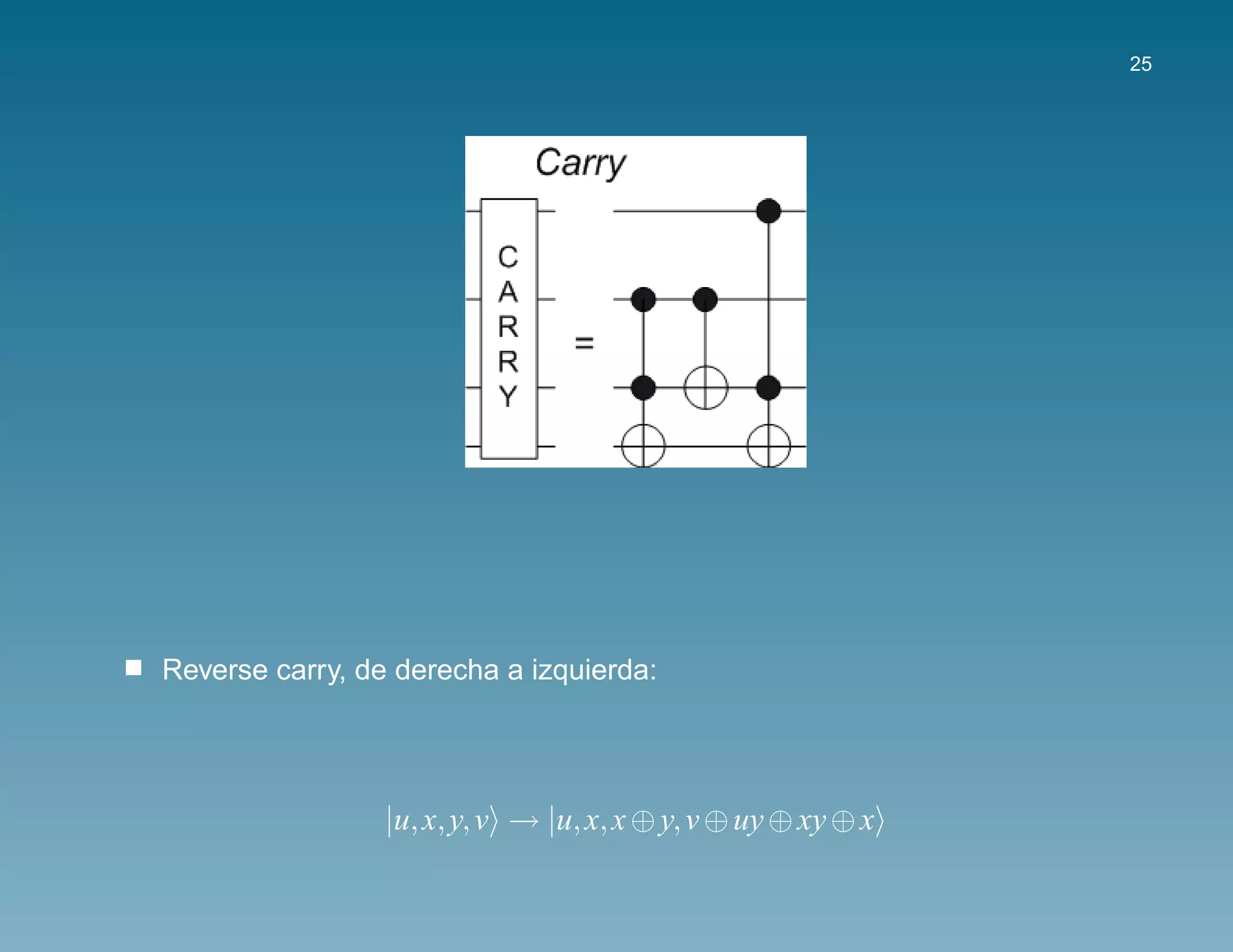
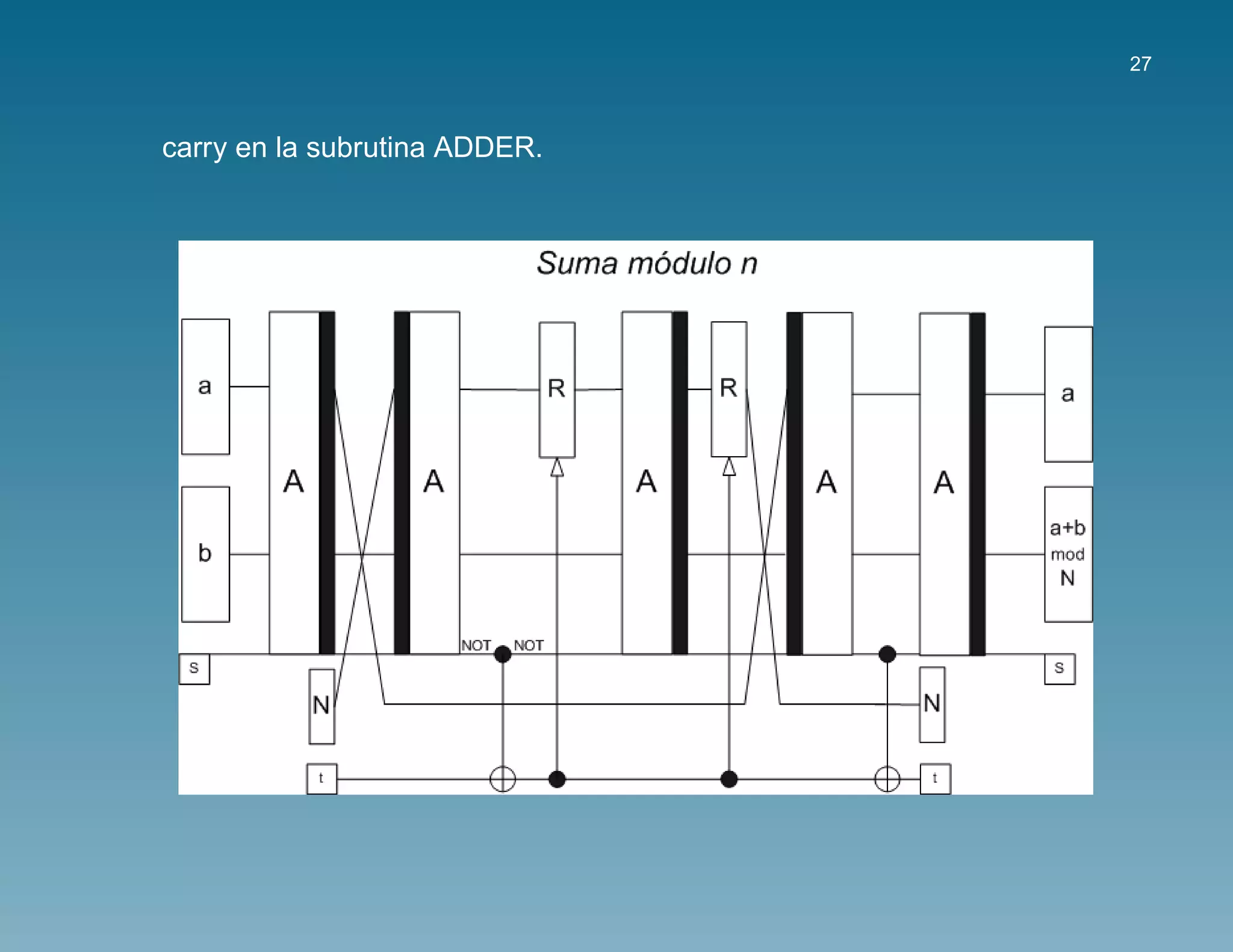
Para conseguir la adiccion modulo N [VBE1996, BCDP1996], necesitaremos
´ ´
un conjunto de circuitos a modo de subrutinas:
´ ´
La suma de dos qubits almacenada en un tercer qubit tambien es facil de

24. 24
conseguir:
|a, b, c → |a, b, a ⊕ b ⊕ c
´ ´
La suma con CARRY es facil de conseguir tambien:
|c, a, b, d = |c, a, a ⊕ b, d ⊕ ab ⊕ ac ⊕ bc

25. 25
Reverse carry, de derecha a izquierda:
|u, x, y, v → |u, x, x ⊕ y, v ⊕ uy ⊕ xy ⊕ x

26. 26
Rutina ADDER:
   
|a, (b) , 0 |a, (a + b) , 0 , (r = 0)
 |a, (b) , 1   |a, (a + b) , 1 , (r = 0) 
 → 
 |a, (b) , 0   |a, (a + b) , 1 , (r = 1) 
|a, (b) , 1 |a, (a + b) , 0 , (r = 1)
Rutina R-ADDER:
   
|u, v, 0 , (u ≤ v) |u, v − u, 0
 |u, v, 1 , (u ≤ v)   |u, v − u, 1 
 → n

 |u, v, 0 , (u > v)   |u, 2 + v − u, 1 
|u, v, 1 , (u > v) |u, 2n + v − u, 0
Finalmente, podemos crear el circuito cuantico para calcular (a + b) modN ,
´
bajo las condiciones de que a y b sean menores que N , con N menor que
2n+1 y s denota el estado de un qubit asociado con un (n + 2)-esimo bit de
´

27. 27
carry en la subrutina ADDER.

28. 28
´
Algoritmos cuanticos: Deutsch-Jozsa
Nos permite distinguir entre funciones constantes y funciones balanceadas
´ ´ ´ ´
asintoticamente mas rapido que en un ordenador clasico[DJ1992].
1. ´
Aleatorizar la configuracion de incio aplicando la transformada de
Hadamard a los n primeros qubits:
2n −1
1
|0, . . . , 0 |0 →
2n/2 ∑ |j |0 .
j=0
2. ´
Evaluar la funcion y almacenar el resultado:
2n −1 2n −1
1 1
2n/2 ∑ |j |0 →
2n/2 ∑ |j | f ( j) .
j=0 j=0

29. 29
3. Aplicar el operador unitario U = σz al ultimo qubit, obteniendo
´
2n −1 2n −1
1 1
2n/2 ∑ | j | f ( j) →
2n/2 ∑ |j (−1) f ( j) | f ( j) .
j=0 j=0
4. ´ ˜´
Reevaluese la funcion y anadase el resultado al ultimo qubit:
´ ´
2n −1 2n −1
1 1
2n/2 ∑ | j (−1) f ( j) | f ( j) →
2n/2 ∑ | j (−1) f ( j) |0 .
j=0 j=0
5. Aplicar la transformada de Hadamard a los primeros n qubits:
2n −1 n 2n −1
1 1 2 −1
2n/2 ∑ | j (−1) |0 → 2n ∑ |u |0
f ( j)
∑ (−1)u· j (−1) f ( j) .
j=0 u=0 j=0

30. 30
La medicion del paso 5 distinguira entre f como funcion constante o
´ ´ ´
balanceada:
Si f es constante, la medicion de los n primeros qubits es u = 0 con prob-
´
abilidad 1, ya que la sumatoria sobre j producir´a 0 para u = 0 y 2n para
ı
u = 0.
Si f es balanceada, la medicion de los n primeros qubits es u = 0 con
´
probabilidad 1, ya que la sumatoria sobre j es 0.

31. 31
´
Algoritmos cuanticos: Grover
Algoritmo de busqueda exhaustivo para datos no ordenados[Grover1996],
´
mejorado en [BBHT1998]: de los O (2n) de un ordenador clasico a los
´
√
O 2n del algoritmo cuantico.
´
√
1. Inicializar n qubits a 0 y el ultimo qubit a |χ ≡ (|0 − |1 ) / 2.
´
2. Aleatorizar los n qubits de entrada tal que
N−1
|0, . . . , 0 |χ → ∑ ak |k |χ = |ψ |χ
k=0
√
donde ak = 1/ N .
3. Repetir los siguientes pasos a y b m veces, donde m ≈ π N/16t siendo
t el numero de soluciones esperadas
´

32. 32
a) Calcular el valor de f con un mapeado unitario U f y anadirlo al ultimo
˜ ´
f (k)
qubit para obtener el factor de fase (−1) :
N−1
|ψ |χ → |ψ U f |χ = ∑ ak |k (−1) f (k) |χ
k=0
b) Aplicar el operador de difusion D = −I + 2J/N al dominio de n qubits,
´
N−1 N−1
∑ ak (−1) ∑ ak |k |χ .
f (k) (1)
|k |χ →
k=0 k=0
4. Medir los qubits del dominio y determinar el estado k, la superposicion se
´
´ ´
perdera tras la medicion
5. Evaluar f (k). S´ f (k) = 1, terminar´a y en cualquier otro caso volver´a al
ı ı ı
paso 1.

33. 33
´
Algoritmos cuanticos: Shor
´ ´ ´
Algoritmo de factorizacion exponencialmente mas rapido que el mejor
´
algoritmo actualmente conocido para ordenadores clasicos[Shor1997]: de
exp c (log (N))1/3 (log (log (N)))2/3 de NFS[LL1993] a una cantidad de
trabajo polinomial en log (N).
1. Elegir n tal que N 2 ≤ S = 2n < 2N 2 e y tal que (y, N) = 1.
2. Inicializar dos registros de n-qubits al estado 0: |ψ0 = |0 |0 .
3. Aleatorizar los primeros n qubits del dominio:
S−1
1
|ψ0 → |ψ1 = ∑ S √ |k |0 .
k=0

34. 34
4. Evaluar la funcion f (k) ≡ yk mod (N) :
´
S−1
1
|ψ1 → |ψ2 = ∑ S √ |k | f (k) .
k=0
5. Transformar los primeros n qubits utilizando la transformada finita de Fouri-
er
1 S−1 S−1
|ψ2 → |ψ3 = ∑ |u ∑ | f (k) exp (2πiuk/S) .
S u=0 k=0
6. Dado que y tiene periodo r, la funcion f es periodica con periodo r: el
´ ´
periodo no tiene porque dividir S, luego escribimos k = m + jr, con 0 ≤
´
m < r y 0 ≤ j < A, con A igualando S , el entero mas pequeno mayor o
r
´ ˜
igual a S . Luego,
r
S−1 r−1
|ψ3 = ∑ ∑ bu exp (2πium/S) |u | f (m) ,
u=0 m=0

35. 35
donde
1 1 − exp (2πiurA/S)
bu = .
S 1 − exp (2πiur/S)
7. Medir el primer registro, obteniendo como antes un valor u con probabili-
dad π3| Pu |ψ3 = rb2.u
8. Interpretar el valor conocido de u enfrentado al valor conocido de S para
deducir el valor putativo de r.
a) Si no se pueden hacer inferencias o r es impar, repetir desde el paso 2.
b) Si r = 2s es par e y2 = −1mod (N), volver al paso 2 y repetir.
c) Usese el algoritmo de Euclides para calcular (N, ys ± 1). Si el resultado
´
es mayor que 1, salir; con cualquier otro valor, volver al paso 2 y repetir.

36. 36
´
De la Teor´a de la Recursion a la
ı
´ ´
Computacion Cuantica
Church-Turing Thesis(1936): “Cualquier procedimiento algor´tmico puede
ı
´ ´
ser simulado por una maquina de Turing”, usando la Maquina Universal de
Turing
Strong Church-Turing Thesis(1960-1970): “Cualquier procedimiento al-
´
gor´tmico puede ser simulado eficientemente por una Maquina de Turing”.
ı
Probabilistic Church-Turing Thesis (1975): “Cualquier procedimiento al-
´
gor´tmico puede ser simulado eficientemente por una Maquina de Turing
ı
probabil´stica”.
ı
Quantum Church-Turing Thesis (1990): “Cualquier procedimiento al-
´
gor´tmico puede ser simulado eficientemente por una Maquina de Turing
ı
´
cuantica”.

37. 37

38. 38
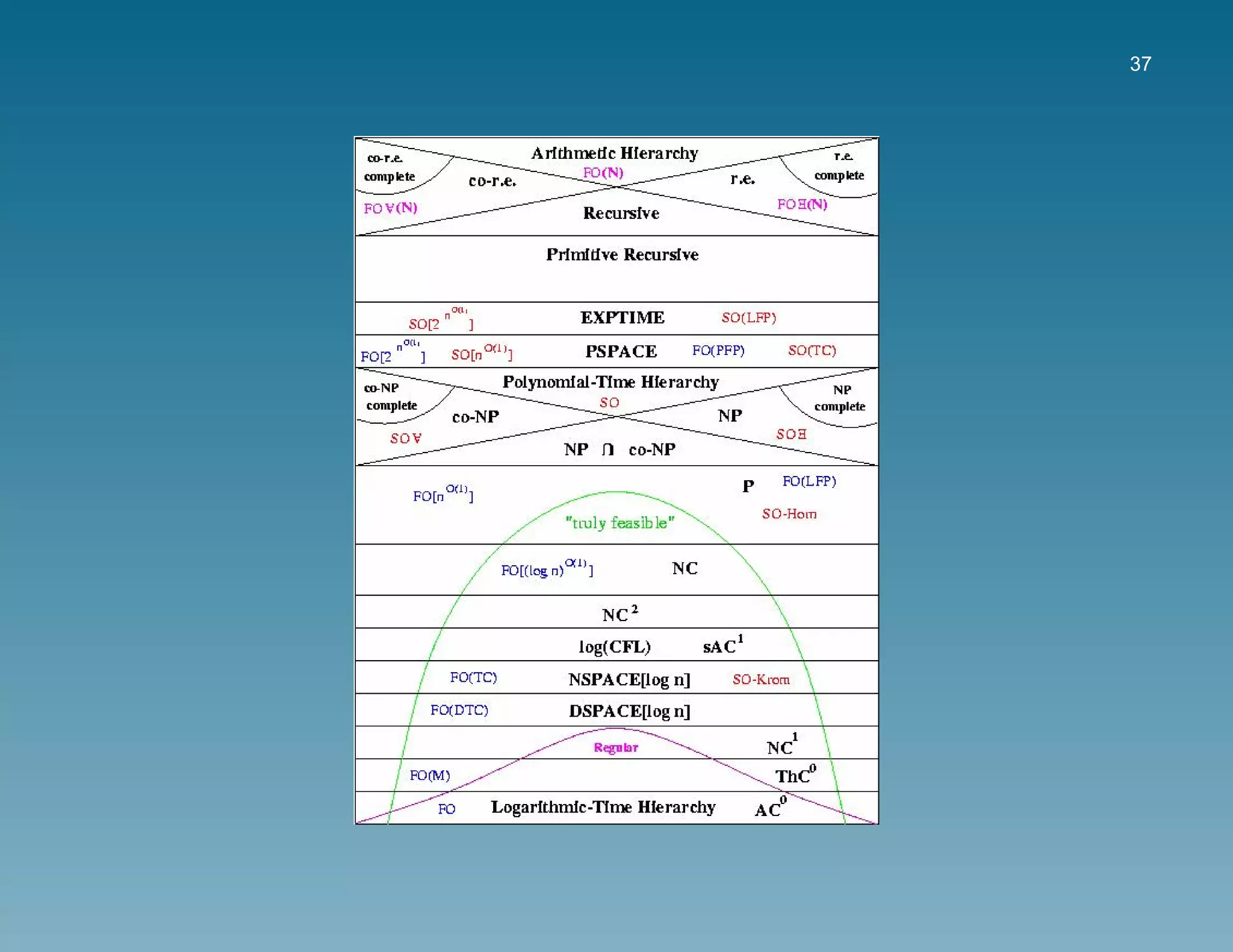
Repaso clases de complejidad
Clase P[Edmons65, Cobham1964, Rabin1960], la clase de problemas de
´ ´
decision resolubles en tiempo polinomial por una maquina de Turing deter-
minista.
Clase NP[Cook1971, Karp1972, Levin1973], es la clase de problemas de
´ ´
decision resolubles en tiempo polinomial por una maquina de Turing inde-
terminista, es decir, que responde con “s´” si al menos un camino acepta y
ı
con “no” si todos los caminos rechazan.
Clase CoNP, es el complemento de la clase NP.
Clase #P[Valiant1979], la clase de problemas de funciones de la forma
“calcular f (X)”, donde f es el numero de caminos aceptadores de la
´
´
maquina NP.

39. 39
´
Clase PP[Gill1977], es la clase de problemas de decision resolubles por
´
una maquina de Turing tal que
Si la respuesta es s´, al menos 1/2 de los caminos de calculo aceptan.
ı ´
Si la respuesta es no, menos de 1/2 de los caminos de calculo aceptan.
´
´
Clase AWPP[FFK1994], la clase de problemas de decision resolubles por
´
una maquina NP tal que
Si la respuesta es no, la diferencia entre el numero de caminos acepta-
´
dores y que rechazan es de como mucho 2-poly(n) f (X)
Si la respuesta es s´, la diferencia es de al menos 1 − 2-poly(n) f (X)
ı
Clase BPP(Bounded-error Probabilistic Polynomial time)[Gill1977], es la
´ ´
clase de problemas de decision resolubles por una maquina NP tal que
La respuesta es s´, si al menos 2/3 de los caminos aceptan.
ı
La respuesta es no, si como mucho 1/3 de los caminos acepta.

40. 40
´
Clase PSPACE, es la clase de problemas de decision resolubles
´ ´
por una maquina de Turing utilizando espacio polinomico. Rela-
ciones: PSPACE=NPSPACE[Savitch1970], PSPACE=AP[CKS1981] y
PSPACE=IP[Shamir90].
´
Clase EXP, es la clase resultante de la union de todos los problemas de
decision resolubles por una maquina de Turing en tiempo 2p(n).
´ ´
´
Clase MA, es la clase de problemas de decision resolubles por un pro-
tocolo de Arthur-Merlin, en el cual Merlin tiene recursos computacionales
´ ˜
ilimitados y manda a Arthur una demostracion de tamano polinomial de
que la respuesta al problema es s´, teniendo que ser comprobada en BPP.
ı
Clase SZK(Statistical Zero-Knowledge)[GMW1991, GMR1989], es la
´
clase de problemas de decision a los que una respuesta afirmativa se
´
puede verificar por un protocolo de demostracion de conocimiento-zero
estad´stico, esto es, un protocolo donde participan un verificador BPP,
ı
Arthur, y un demostrador, Merlin, con recursos computacional ilimitados,

41. 41
y en el que Arthur debe convencerse de la que respuesta es s´ intercam-
ı
´ ´
biandose mensajes con Merlin, sin llegar a saber nada mas del problema.

42. 42
´
Nuevas clases cuanticas de complejidad
Clase BQP (Bounded-error Quantum Polynomial time)[BV1997, Yao1993],
´
es la clase de problemas de decision resolubles en tiempo polinomico´
por una maquina de Turing cuantica, con como mucho 1/3 de probabil-
´ ´
´
idad de error. Algunos problemas de esta clase son la factorizacion de
enteros y el problema del logaritmo discreto[Shor1997], el s´mbolo de Leg-
ı
´
endre oculto[DHI2002], la ecuacion de Pell y los problemas de ideales
principales[Hallgren2002].
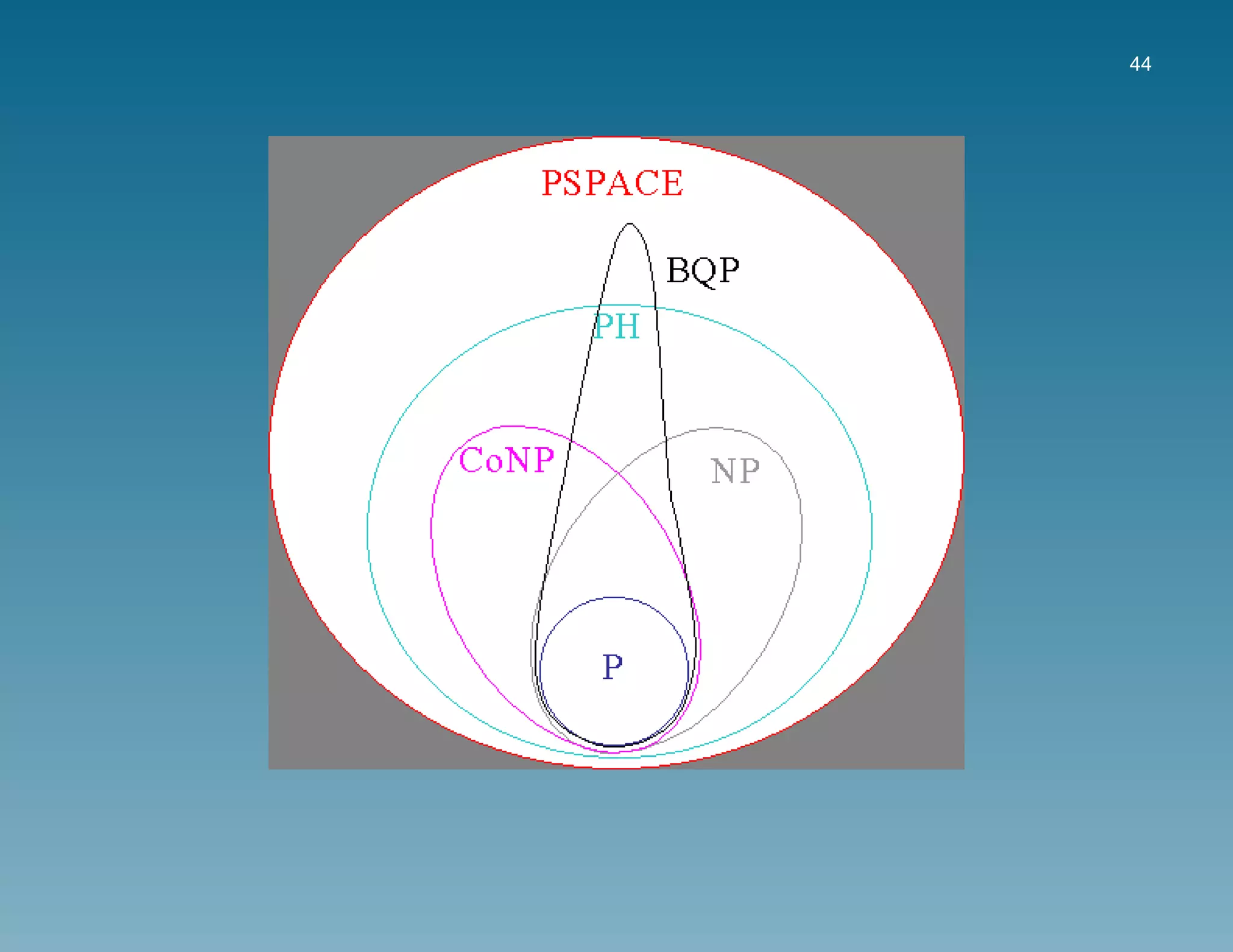
Relaciones de BQP con otras clases de complejidad:
P ⊆ BQP
BPP ⊆ BQP[BV1997]
BQP ⊆ PSPACE
P ⊆ BPP ⊆ BQP ⊆ PSPACE

43. 43
BQP ⊆ P#P[BV1997]
BQPBQP = BQP[BV1997]
BQP ⊆ PP[ADH97]qu
BQP ⊆ AWPP[FR1998]
BQP/qpoly ⊆ EXP/poly[Aaronson2003]
´
Existen oraculos relativos a los cuales:
BPP = BQP[BV1997]
BQP MA[Watrous2000]
BQP Mod pk P[GV2002]
NP BQP y NP∩CoNP BQP[BBBV1997]
SZK BQP[Aaronson2002]

44. 44

45. 45
´ ı
Realizacion f´sica de ordenadores
´
cuanticos
Sobre las dificultades [DivS1995]. Requisitos:
´ ´ ´ ´
Representacion fidedigna de la informacion cuantica: aunque es teorica-
´
mente posible almacenar una cantidad infinita de informacion, cuando hay
´
ausencia de ruido, en realidad solo se puede aspirar a un conjunto finito de
´
estados para almacenar informacion porque el ruido reduce el numero de
´
´
estados distinguibles. Habra que tener en cuenta el tiempo de vida m´nimo
ı
´
de una superposicion arbitraria de estados.
Posibilidad de ejecutar alguna familia universal de transformaciones uni-
tarias: operaciones sobre qubits individuales y puertas CNOT. Las imper-
´ ´
fecciones en la aplicacion de alguna transformacion unitaria nos lleva a
´ ´
la decoherencia. Habra que considerar el tiempo maximo requerido para

46. 46
´
realizar una operacion elemental y fidelidad alcanzable m´nima, siendo la
ı
fidelidad de dos estados ρ, σ,
F (ρ, σ) ≡ tr ρ1/2σρ1/2
Posibilidad de preparar un estado inicial confiable: el aumento de tem-
peratura y el resto de operaciones mientras se prepara el estado inicial,
´
puede llevar a la decoherencia. Parametros a tener en cuenta son la fi-
delidad m´nima con la que el estado inicial puede ser preparado dado un
ı
estado ρin y la entrop´a de ρin.
ı
´
Posibilidad de medir el resultado de salida: se realizara uniendo uno o
´ ´
varios qubits a un sistema clasico que cambiara su estado tras un deter-
minado periodo de tiempo. Las imprecisiones en los aparatos de medida,
´ ´ ´
el ruido termico... produciran decoherencia. El principal parametro a tener
´ ˜
en cuenta sera el ratio senal/ruido (SNR).:

47. 47
´ ´
Ordenador cuantico de fotones opticos
´ ´
Siguiendo la descripcion de [CY1995], el foton es una part´cula sin carga
ı
´ ´
que interactua debilmente con toda la materia y se obtendran atenuando la
´
salida de un LASER[IY1994, KSCEP1994]. El estado |ψ = c0 |0 + c1 |1
´
del foton evoluciona en el tiempo para convertirse en
|ψ (t) = c0 |0 + c1e−iωt |1 ,
usando diferentes mecanismos: trozos de material transparente con un
´ndice de refraccion n para el cambio de fase; piezas de vidrio parcialmente
ı ´
plateadas que reflecten una fraccion R de la luz incidente y transmitan
´
1 − R, como beamsplitter, que se suele fabricar usando prismas con una
´
capa metalica entre ella; y, por ultimo, un medio no-lineal de Kerr en los
´
que el ´ndice de refraccion es preoporcional a la intensidad total de luz I
ı ´
´
que pasa por este,
n (I) = n + n2I.

48. 48
´
Los Hamiltonians para los diferentes componentes del sistema seran:
Cambio de fase con mecanismo P: H = (n0 − n) Z donde P =
exp (−iHL/c0) .
Beamsplitter : Hbs = iθ ab† − a†b , llevando a cabo la operacion uni-
´
taria B = exp θ a†b − ab† .
Medio de Kerr no lineal: H pm = −χa†ab†b, siendo la transformacion uni-
´
† †
taria K = eiχLa ab b.
Combinando el medio de Kerr con el beamsplitter se puede obtener puer-
´
tas CNOT y las operaciones sobre un unico qubit se realizaran mediante
´
´ ´
cambios de fase y beamsplitters. Un ejemplo de realizacion practica es
[KMSW1999].
Limitaciones:
´ ´
la representacion de qubits mediante un unico foton es simple y atrac-
´
tiva, pero los medios de Kerr disponibles actualmente son demasiado
´
debiles[WY1990].

49. 49
´ ´
Electrodinamica cuantica de cavidades
´
opticas
´ ´
Tanto la representacion de los qubits como la preparacion de los esta-
´ ´
dos iniciales es igual que en un ordenador cuantica fotonico, pero en las
´
transformaciones unitarias se buscara reemplazar los deficientes medios
´
de Kerr, buscando conseguir transferir el estado de un foton a otro usando
las cavidades de Fabry-Perot, cuyo Hamiltonian es
ω0
H= Z + ωa†a + g a†σ− + aσ+
2
donde ω es la frecuencia del campo, ω0 la frecuencia del atomo y g la
´
´
constante de acoplamiento entre atomo y campo.
´
Limitaciones: el acoplamiento de dos fotones es mediado por un atomo,
´
haciendo deseable incrementar el acoplamiento atomo-campo, pero en-

50. 50
´
tonces el acoplamiento del foton dentro y fuera de la cavidad se dificulta y
limita la cascabilidad.
´
Experimentos practicos en [THLMK1995, TPhD1997].

51. 51
Trampas de iones
´
Propuesto en [CZ1995], la representacion de qubits se realiza mediante el
´ ´ ´
spin del nucleo del atomo y modos de vibracion de bajo nivel de atomos
´

52. 52
atrapados. Dibujo basado en [WMILKM1998].
´
La evolucion unitaria del sistema se consigue con pulsos LASER que ma-
´ ´
nipulan externamente el estado atomico, segun la interaccion de Jaynes-
´
Cummings. Los qubits interactuan mediante estados compartidos de
´
fonones. Hamiltonian:
Ω

η √
i N
S+a†eiϕ − S−ae−iϕ ω = ω0 + ωz

HI = 2
Ω
η √
i N
S+aeiϕ − S−a†e−iϕ ω = ω0 − ωz

2
´ ´
Para preparar el estado inicial se enfriaran los atomos hasta que su en-
´ ´ ´
erg´a cinetica sea mucho menor que la contribucion energetica del spin.
ı
Experimentos en [WMILKM1998, MMKIW1995].
Limitaciones:

53. 53
´
El tiempo de vida del fonon es demasiado corto.
´
Dificultades en la prepacion de los iones en su estado inicial[MMKIW1995,
J1998].

54. 54
´
Resonancia magnetica nuclear

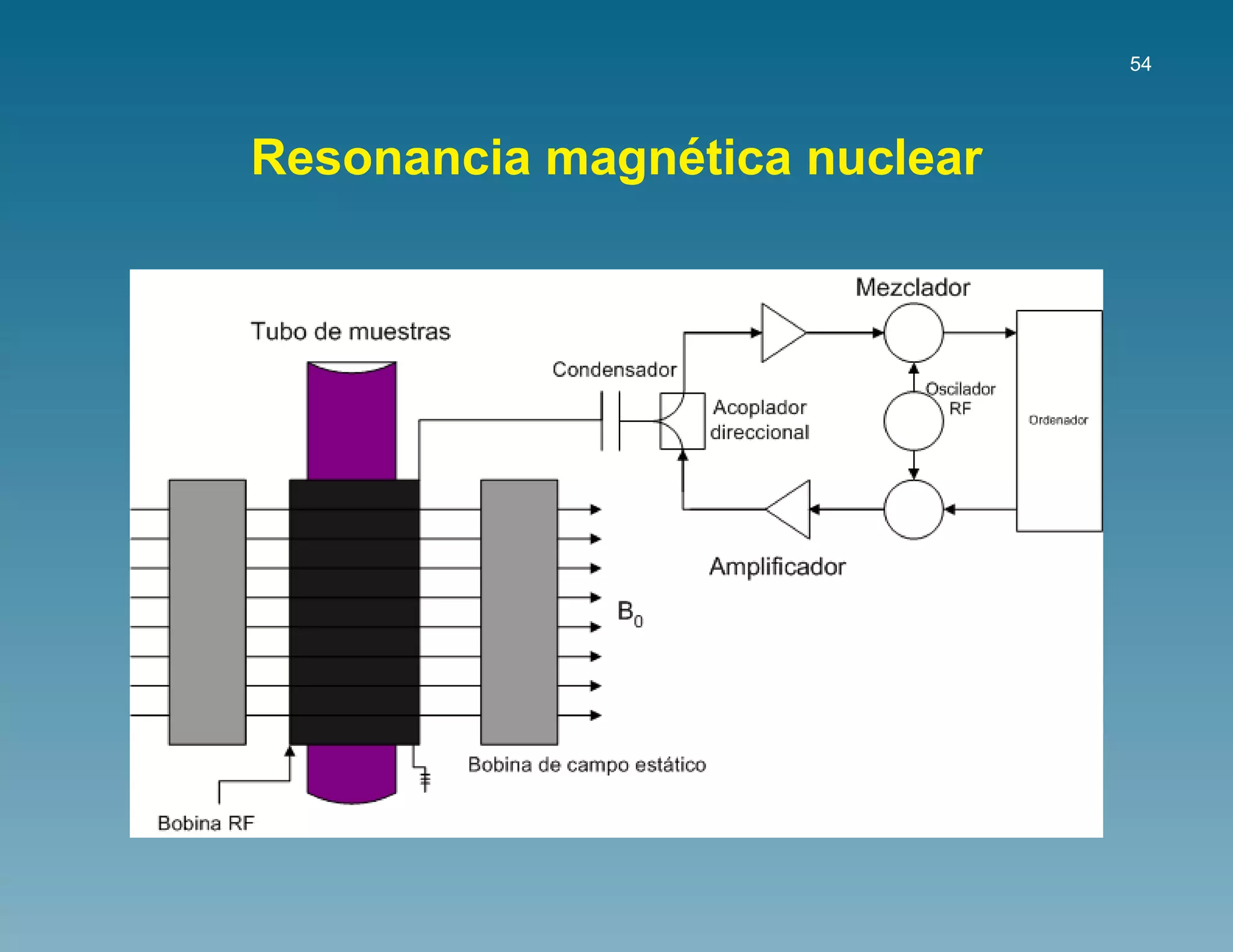
55. 55
´ ´ ´
La representacion de los qubits usara el spin de nucleos atomicos[DiVincenzo1995].
´
´
La evolucion unitaria del sistema se consigue con pulsos de cam-
´ ´
pos magneticos aplicados a spins en fuertes campos magneticos. Los
´
acoplamientos entre spins se realizan con uniones qu´micas entre los ato-
ı
mos vecinos. Hamiltonian:
H = ∑ ωk Zk + ∑ H J + H RF + ∑ H D + H env
j,k j,k
k j,k j,k
donde H Des el acoplamiento del dipolo magnetico, H J es el J -
´
acoplamiento, H RF son los efectos los campos magneticos de radiofre-
´
cuencia externos y H env describe interacciones con el entorno que pueden
llevar a la decoherencia.
´ ´
La preparacion del estado inicial consiste en polarizar los spins colocando-
´ ´
los en un fuerte campo magnetico, luego utilizar las tecnicas de “estado
puro efectivo”. Opera a temperatura ambiente[CFH1997, GC1997].

56. 56
Experimentos [CGK1998, VYSC1999, CVZLL1998, CMPAl1998, STHAl1999,
LVZAl1999, JM1998, JMH1998].
Limitaciones:
´ ˜
La preparacion de “estados puros efectivos” reducen la senal exponen-
´
cialmente en proporcion al numero de qubits, a no ser que la polar-
´
´
izacion inicial sea lo suficientemente grande.
´ ı ´
Multiples cr´ticas a esta implementacion [W1997, SC1999, BCJLPS1999,
Vid1999, KHSL1999, LP1999].

57. 57
´
V´deo: simulacion 2-qubit NMR QC
ı

58. 58
´
V´deo: simulacion 2-qubit ideal QC
ı

59. 59
´
Decoherencia y comparacion entre
´
metodos
´ ´ ´
La decoherencia, o ruido cuantico, se define como la destruccion de la superposicion de
´ ´ ´
estados cuanticos por la interaccion del entorno en el sistema cuantico aislado, vg:
aumento de temperatura... En la siguiente tabla se recogen estimaciones del tiempo de
decoherencia y numero de operaciones.
´
τ
´
Implementacion τQ τop nop = λ−1 = τop
Q
Spin del nucleo
´ 10−2 − 10−8 10−3 − 10−6 105 − 1014
´
Spin del electron 10−3 10−7 104
Trampa de iones 10−1 10−14 1013
´
Electron - Au 10−8 10−14 106
´
Electron - GaAs 10−10 10−13 103
Quantum dots 10−6 10−9 103
´
Cavidad optica 10−5 10−14 109
Cavidad de Microondas 100 10−4 104
´
Electron-Nuclear en Si 101 10−4 − 10−5 105 − 106

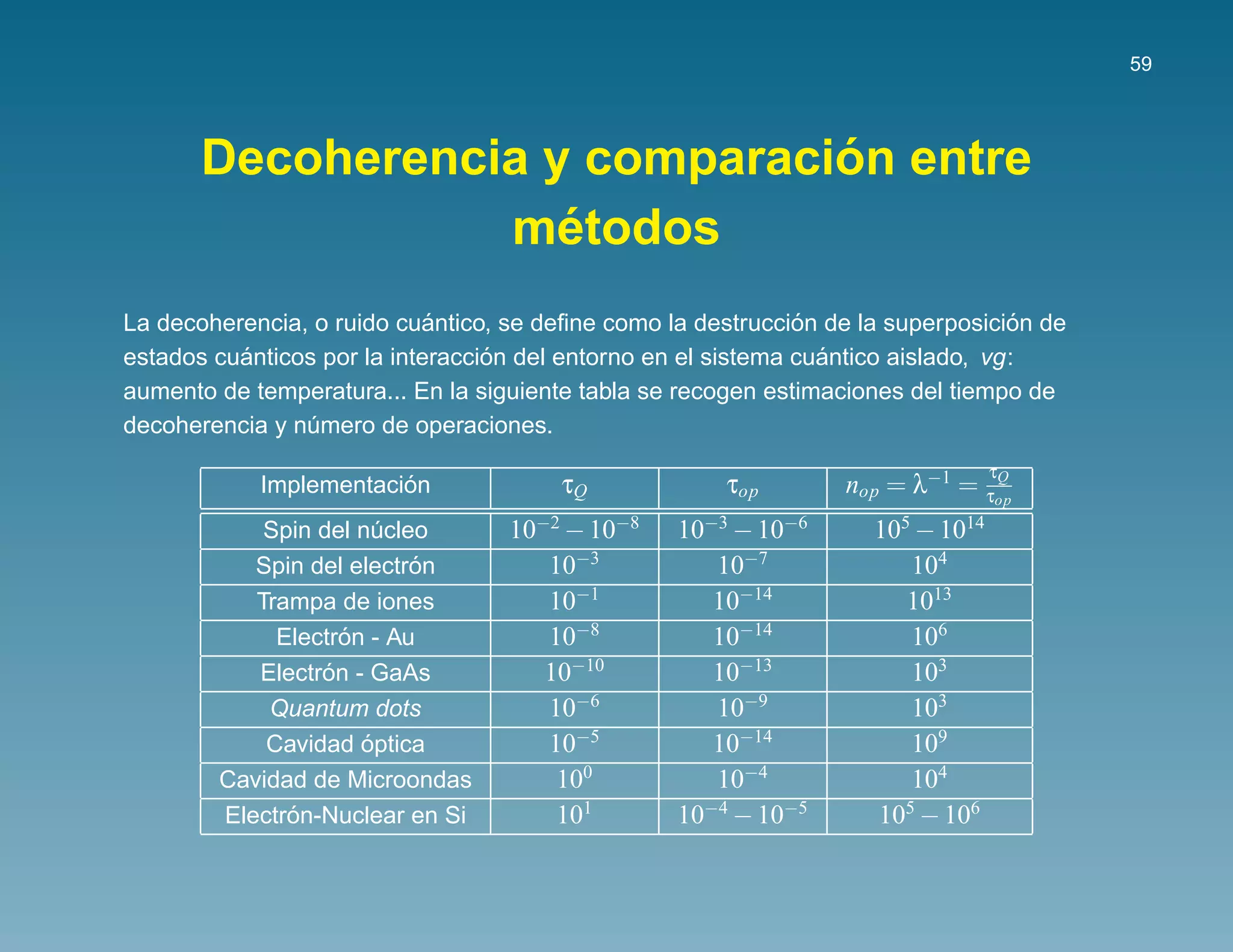
60. 60
´
Fundamentos teor´a de la informacion
ı
´
cuantica
Resultados fundamentales:
´
Teorema No-Cloning[Dieks1982, WZ1982]: ningun dispositivo cuanti-
´
co puede tener como salida |ψ |ψ , dado el estado |ψ , para un |ψ
cualquiera.
Cota de Holevo[Gordon64, Holevo1973, FC1994, YO1993, SWW1996]:
´ ´ ´
El maximo de informacion clasica accesible cuando se intenta distinguir
entre estados cuanticos px enviados con probabilidades de distribucion px
´ ´
es
H (X : Y ) ≤ χ ≡ S ∑ px px − ∑ pxS (px) .
x x

61. 61
´ ´
Teorema de Schumacher de la codificacion de canales cuanticos sin
ruido[Schumacher1995]: S (p) puede ser interpretado como el numero de
´
´
qubits necesitados para representar fielmente una fuente de informacion
cuantica descrita por p.
´
Teorema de Holevo-Schumacher-Westmoreland[Holevo1979, HJSW1996,
´
Holevo1998, SW1997]: la capacidad de un canal de comunicacion cuanti- ´
co ε con ruido para la transmision de informacion clasica viene dada por
´ ´ ´
C (ε) = m´ x S
a
{px ,|ψx }
∑ pxε (|ψx ψx|) − ∑ pxS (ε (|ψx ψx|)) (3)
x x

62. 62
´ ´
Teor´a de la informacion clasicas y
ı
´
cuanticas
´ ´ ´
En teor´a de la informacion clasica, la entrop´a viene dada por la formula de
ı ı
Shannon[SW1949]
H (X) = − ∑ p (x) log p (x) ,
x
´ ´
y en teor´a de la informacion cuantica, se utiliza la entrop´a de von Neumann,
ı ı
S (p) = −tr (ρ log ρ) .
´ ´
La cantidad de informacion distinguible, es decir, la informacion accesible, en
informacion clasica es N = |X|, y en informacion cuantica se usa la cota de
´ ´ ´ ´
Holevo[Gordon64, Holevo1973, FC1994, YO1993, SWW1996],
H (X : Y ) ≤ S (∑x px px) − ∑x pxS (px).
´ ´ ´
La codificacion de canales sin ruido en informacion clasica viene dada por el

63. 63
teorema de Shannon[SW1949, Sha1948],
nbits = H (X) ,
´ ´
y en informacion cuantica utilizamos el teorema de Schumacher
[Schumacher1995],
nqubits = S ∑ px px .
x
´
La capacidad de un canal clasico con ruido viene dado por un teorema de
Shannon,
C (N) = m´ x H (X : Y ) ,
a
p(x)
´ ´
y en informacion cuantica, por el teorema
Holevo-Schumacher-Westmoreland3,
C (ε) = m´ x S
a
{px ,|ψx }
∑ pxε (|ψx ψx|) − ∑ pxS (ε (|ψx ψx|)) .
x x

64. 64
´ ´
Algunas relaciones interesantes en teor´a de la informacion clasica, con sus
ı
´ ´
equivalentes en informacion cuantica, son:
´
Inecuacion de Fano,
H (pe) + pe log (|X| − 1) ≥ H (X|Y ) ,
´ ´
y la inecuacion de Fano cuantica,
H (F (ρ, ε)) + (1 − F (ρ, ε)) log d 2 − 1 ≥ S (ρ, ε) .
´ ´
Informacion mutua clasica,
H (X : Y ) = H (Y ) − H (Y |X) ,
´ ´
y la informacion coherente cuantica,
I (ρ, ε) = S (ε (ρ)) − S (ρ, ε) .

65. 65
´ ´
Inecuacion en el proceso de datos clasico,
X →Y →Z
H (X) ≥ H (X : Y ) ≥ H (X : Z) ,
´ ´
y la inecuacion en el proceso de datos cuanticos[SN1996],
ρ → ε1 (ρ) → (ε2 ◦ ε1) (ρ)
S (ρ) ≥ I (ρ, ε1) ≥ I (ρ, ε2 ◦ ε1) .

66. 66
´
Criptograf´a cuantica: historia
ı
Las primeras ideas datan de 1960[Wiesner1960, Wiesner1983]: uso como dinero
´
electronico seguro.
´
Amplificacion de la privacidad[BBR1988].
´ ´
Protocolos de reconcialiacion de la informacion[BS1994].
´
Primera implementacion experimental[BBBSS1992].
´
Protocolos mas conocidos: de cuatro estados[BB1984], de dos estados [Bennet1992] y
basado en EPR[Ekert1991].
Demostraciones de los protocolos: completa del BB84[Mayers1998], usando EPR y
´ ´
computacion cuantica perfecta[LC1999].
´ ´
Posteriores implementaciones: introduccion[HADLMS1995], implementacion del lago de
Ginebra[MZG1996], implementaciones de IBM[BE1998, WR2000].

67. 67
´ ´
Distribucion de claves cuantica QKD
Puntos sobre los que se apoya QKD:
´ ´ ´
Reconciliacion de la informacion[BS1994]: correcion de errores sobre
un canal publico cuantico, reconcialiando los errores entre X e Y , para
´ ´
obtener una cadena de bits compartida entre W , divulgando la menor can-
´
tidad de informacion posible a Eve.
Amplificacion de la informacion[BBR1988]: distila la informacion W ,
´ ´ ´
´ ´ ´
cuya correlacion con la informacion obtenida por Eve esta por debajo de un
l´mite fijado por Alice y Bob. Dada una funcion g de las funciones de hash
ı ´
universales, escogida uniforme y aleatoriamente, que asigna las cadenas
de n-bits de A con las cadenas de m-bits de Bob, tal que para cualquier
a1, a2 ∈ A la probabilidad de que g (a1) = g (a2) es de como mucho 1/ |B|.
La entrop´a de la colision de la variable aleatoria X con distribucion de
ı ´ ´
probabilidad p (x) es

68. 68
Theorem 3. Sea X la variable aleatoria en el alfabeto χ con la distribu-
cion p (x), la entrop´a de la colision Hc (X) y G la variable aleatoria correspon-
´ ı ´
´
diente a la opcion aleatoria de un miembro de la clase universal de funciones
de hash desde χ a {0, 1} , entonces
m
H (G (X) |G) ≥ Hc (G (X) |G) ≥ m − 2m−Hc(X).
´
Este teorema nos indica que si Alice y Bob eligen publicamente g ∈ G y la
´
aplican a W , obteniendo S, podr´an maximizar la incertidumbre de Eve sobre
ı
S, cuyo conocimiento sobre S esta en Z = z, y que es estimado por Alice y
´
´ ´ ´
Bob en terminos de la entrop´a de la colision, limitandola inferiormente un
ı
numero d , Hc (S|W, Z = z) > d , y por el teorema anterior,
´
Hc (S|G, Z = z) ≥ m − 2m−d ,
es decir, elegir m tal que Hc (S|G, Z = z) m.

69. 69
Corollary 2. ´ ´
Por argumentos estad´sticos de informacion clasica para
ı
´ ´ ´ ´
la reconciliacion de informacion, seguido de la amplificacion de la informacion,
podremos conseguir m bits secretos entre Alice y Bob, para los cuales la
´
informacion total de Eve es menor que
2m−d+2(k+s)bits,
donde s es un parametro de seguridad a escoger y k el numero de bits en-
´ ´
´ ´ ´
viados durante el proceso de reconciliacion como codigos de correcion de
errores.
Eve no puede distinguir entre estados dos estados cuanticos no- ´
˜
ortogonales transmitidos de Alice a Bob sin perturbar la senal. Por lo tanto,
´
Alice y Bob introduciran qubits de prueba en posiciones aleatorias de la
´
transmision para establecer una cota superior en el ruido o espionaje en el
´
canal. Luego llevan a cabo un proceso de reconciliacion de la informacion ´
´
y de amplificacion de la privacidad para destilar una clave secreta compar-
´
tida entre ambos, con el conocimiento de Eve sobre esta perfectamente

70. 70
´
acotado, y con posibilidad de detectar cuando se esta intentando romper
´
la seguridad de la comunicacion.
´
El unico requerimiento sera que el protocolo QKD se ejecute sobre un
´
canal publico con una tasa de error por debajo de un l´mite fijado.
´ ı
´
Descripcion del protocolo BB84[BB1984]:
1. Alicia crea (4 + δ) n bits aleatorios.
2. Por cada bit, crea un qubit en la base Z o en la base X , segun una cadena
´
de bits aleatoria b.
3. Alicia env´a los qubits a Bob.
ı
4. Alicia elige aleatoriamente una vk ∈ C1, un codigo clasico, para llevar a
´ ´
´ ´
cabo reconciliacion de la informacion.

71. 71
5. Bob recibe los qubits y los mide en las bases X y Z aleatoriamente.
6. Alicia anuncia b.
7. ´
Alicia y Bob descartan aquellos bits que Bob midio en una base diferente
a b, quedando con alta probabilidad 2n bits, abortandose si no ocurre as´.
´ ı
Alicia escoge n bits y los anuncia, entre los 2n bits.
8. Alicia y Bob comparan publicamente sus bits de chequeo: si mas de t bits
´ ´
estan en desacuerdo, el protocolo aborta. Alicia quedara con un cadena x
´ ´
de n bits y Bob con x + ε.
9. Alicia anuncia x − vk . Bob resta esto de su resultado, corrigiendolo con C1
´
para obtener vk .
10. Alicia y Bob calculan el co-conjunto de vk +C2 en C1 para obtener la clave
k.

72. 72
Referencias
[NCBook] Nielsen, Michael and Chuang, Isaac L. “Quantum
Computation and Quantum Information“
[FeynmanBook] Richard P. Feynman, “Feynman lectures on com-
putation”
[GruskaBook] Gruska, J. “Quantum Computing”
[WCBook] C. Williams and S. Clearwater, “Explorations in
Quantum Computing”
[GramssBook] T. Gramss, “Non-Standard Computation”
[RPIntro] E. Rieffel and W. Polak, “An introduction
to Quantum Computing for Non-Physicists”
http://xxx.lanl.gov/abs/quant-ph/9809016

73. 73
[Savitch1970] W. Savitch. Relationships between nondetermin-
istic and deterministic tape complexities. Jour-
nal of Computer and System Sciences 4(2):177-
192, 1970.
[CKS1981] A. K. Chandra, D.C. Kozen, and L.J. Stockmey-
er. Alternation. Journal of the ACM 28:114-133,
1981.
[Shamir90] A. Shamir. IP=PSPACE. Proceedings of the
IEEE FOCS’90, pp. 11-15, 1990.
[Edmons65] J. Edmons. Paths, trees and flowers, Canadian
Journal of Mathematics 17(3):449-467, 1965.
[Cobham1964] A. Cobham. The intrinsic computational difficulty
of functions. Proceedings of the 1964 Congress

74. 74
on Logic, Mathematics and the Methodology of
Science, pp. 24-30, 1964.
[Rabin1960] M. O. Rabin. Degree of difficulty of computing a
function and a partial ordering of recursive sets,
Technical Report No. 2, Hebrew University, 1960.
[Cook1971] S. A. Cook. The complexity of theorem-proving
procedures. Proceedings of the ACM STOC’71,
pp. 151-158, 1971.
[Karp1972] R. M. Karp. Reducibility among combinatorial
problems. Complexity of Computer Computa-
tions (J. W. Thatcher and R. E. Miller, eds.),
Plenum Press, 1972.
[Levin1973] L. A. Levin. Universal search problems (in Rus-
sian), Problemy Pederachi Informatsii 9(3):265-
266, 1973.

75. 75
[Gill1977] J. Gill. Computational Complexity of Turing
machins. SIAM Journal of Computing 6(4):675-
695, 1977.
[BV1997] E. Bernstein and U. Vazirani. Quantum com-
plexity theory, SIAM Journal of Computing,
26(5):1411-1473, 1997.
[Yao1993] A.C.-C. Yao. Quantum circuit complexity. Pro-
ceedings of IEEE FOCS’93, pp.352-361, 1993.
[Shor1997] P. Shor. Polynomial time algorithms for prime
factorization and discrete logarithms on a quan-
tum computer. SIAM Journal on Computing
26(5):1484-1509, 1997. quant-ph/9508027

76. 76
[DHI2002] W. van Dam, S. Hallgren, L. Ip. Quantum al-
gorithms for hidden coset problems, submitted,
2002.
[Hallgren2002] S. Hallgren. Polynomial-time quantum algorithms
for Pell’s equation and the principal ideal prob-
lem. Proceedings of ACM STOC’2002, 2002.
[ADH97] L. Adleman, J. DeMarrais, and M. Huang. Quan-
tum computability. SIAM Journal of Computing
26:1524-1540, 1997.
[FR1998] L. Fortnow and J.D. Rogers. Complexity lim-
itations on quantum computation. Proceed-
ings of IEEE Complexity’98, pp. 202-209, 1998.
cs.CC/9811023

77. 77
[Watrous2000] J. Watrous. Succint quantum proofs for prop-
erties of finite groups. Proceedings of IEEE
FOCS’2000 cs.CC/0009002
[GV2002] M. de Graaf and P. Valiant. Comparing EQP and
Mod pk P using polynomial degree lower bounds, 2002. qua
[BBBV1997] C.H.Bennet, E. Bernstein, G. Brassard, and
U. Varizani. Strengths and weakness of quan-
tum computing. SIAM Journal on Computing,
26(5):1510-1523, 1997. quant-ph/9701001
[Aaronson2002] S. Aaronson. Quantum lower bounds for the colli-
sion problem. Proceedings of ACM STOC’2002,
pp. 635-642, 2002. quant-ph/0111102
[Aaronson2003] S. Aaronson. BQP/qpoly is contained in
EXP/poly. Complexity’2003, Denmark, July

78. 78
8, 2003. http://www.cs.berkeley.edu/ aaron-
son/qpoly.ppt
[Valiant1979] L. G. Valiant. The complexity of computing
the permanent. Theoretical Computer Science,
8:189-201, 1979.
[FFK1994] S. Fenner, L. Fortnow, and S. Kurtz. Gap-
definable counting classes. Journal of Computer
and System Sciences 48(1):116-148, 1994.
[GMW1991] O. Goldreich, S. Micali, and A. Wigderson. Proofs
that wield nothing but their validity or all lan-
guages in NP have zero-knowledge proof sys-
tems, Journal of the ACM 38(1):691-729, 1991.
[GMR1989] S. Goldwasser, S. Micali, and C. Rackoff. The
knowledge complexity of interactive proof sys-

79. 79
tems, SIAM Journal of Computing 18(1):186-
208, 1989.
[DiVincenzo1995] David DiVincenzo. Two-bit gates are universal
for quantum computation, Physical Review A, vol
151, 1015-1022 (1995).
[VBE1996] Vlatko Vedral, Adriano Barenco, Artur Ekert.
Quantum networks for elementary arithmetic op-
erations. Physical Review A. vol 54, 147. (1996).
[BCDP1996] David Beckman, Amalavoyal N. Chari, Srikrishna
Devabhaktuni, John Preskill. Efficient networks
for quantum factoring. Physical Review A. vol. 54,
no. 2, 1034-1063, Aug 1996.
[Dieks1982] D. Dieks. Communication by EPR devices. Phys-
ical Letters A, 92(6):271-272, 1982.

80. 80
[WZ1982] W.K. Wootters, W. H. Zurek. A single quantum
cannot be cloned. Nature, 299:802-803, 1982.
[Gordon64] J.P. Gordon. Noise at optical frequencies; infor-
mation theory. En P.A. Miles, editor, Quantum
Electronics and Coherent Light, Proceedings of
the International School of Physics “Enrico Fer-
mi” XXXI, Academic Press, New York, 1964.
[Holevo1973] A.S. Holevo. Statistical problems in quan-
tum physics. En Gisiro Maruyama y Jurii V.
Prokhorov, editores, Proceedings of the Second
Japan-USSR Symposium on Probability Theory,
´
paginas 104-119, Springer-Verlag, Berlin, 1973.
Lecture Notes in Mathematics, vol. 330.
[FC1994] C.A. Fuchs y C.M. Caves. Ensemble-dependent
bounds for accesible information in quantum me-

81. 81
chanics. Physical Review Letters, 73(23):3047-
3050, 1994.
[YO1993] H.P. Yuen y M. Ozawa. Ultimate information car-
rying limit of quantum systems. Physical Review
Letters, 70:363-366, 1993.
[SWW1996] B.W. Schumacher, M. Westmoreland, W.K.
Wootters. Limitation on the amount of accessi-
ble information in a quantum channel. Physical
Review Letters, 76:3453, 1996.
[Schumacher1995] B. Schumacher. Quantum coding. Physical Re-
view A, 51:2738:2747, 1995.
[Holevo1979] A.S. Holevo. Capacity of a quantum communica-
tions channel. Problems of Information Transmis-
sion, 5(4):247-253, 1979.

82. 82
[HJSW1996] P. Hausladen, R. Jozsa, B. Schumacher, M.
Wetsmoreland, W.K. Wootters. Classical infor-
mation capacity of a quantum channel. Physical
Review A, 54:1869, 1996.
[Holevo1998] A.S. Holevo. The capacity of the quantum chan-
nel with general signal states. IEEE Transactions
on Information Theory, 44(1):269-273, 1998.
[SW1997] B. Schumacher and M.D. Westmoreland. Send-
ing classical information via noisy quantum chan-
nels. Physical Review A, 56(1):131-138, 1997.
[Wiesner1960] S. Wiesner. Unpublished manuscript, 1969.
[Wiesner1983] S. Wiesner. Conjugate coding. SIGACT News,
15:77, 1983.

83. 83
[BBBSS1992] C.H. Bennet, F. Bessette, G. Brassard, L. Salvail,
J. Smolin. Experimental quantum cryptography.
Journal of Cryptology, 5:3-28, 1992.
[BBR1988] C.H. Bennet, G. Brassard, J.M. Robert. Privacy
amplification by public discussion. SIAM Journal
of Computing, 17:210-229, 1988.
[BS1994] G. Brassard, L. Salvail. Secret-key reconcilia-
tion by public discussion. Lecture notes in com-
puter science: Advances in Cryptology - EU-
ROCRYPT’93, Volume 765, 410-423, Springer-
Verlag, New York, 1994.
[BB1984] C.H.Bennet, G. Brassard. Quantum cryptogra-
phy: public key distribution and coin tossing.
Proceedings of IEEE International Conference
on Computers, Systems and Signal Processing,

84. 84
175-179, IEEE, New York, 1984. Bangalore, In-
dia, Dec 1984.
[Bennet1992] C.H. Bennet. Quantum cryptography using any
two nonorthogonal states. Physical Review Let-
ters, 68(21):3121-3124, 1992.
[Ekert1991] A.K. Ekert. Quantum cryptography based
on Bell’s theorem. Physical Review Letters,
67(6):661-663, 1991.
[HADLMS1995] R.J. Hughes, D.M. Alde, P. Dyer, G.G. Luther,
G.L. Morgan, M. Schauer. Quantum cryptog-
raphy. Contemporary Physics, 36(3):149-163,
1995. quant-ph/9504002
[MZG1996] A. Muller, H. Zbinden, N. Gisin. Quantum cryp-
tography over 23 km. installed under-lake tele-

85. 85
com fibre. Europhysics Letters, 33:334-339,
1996.
[BE1998] D.S. Bethune, W.P. Risk. An autocompensating
quantum key distribution system using polariza-
tion splitting of light. IQEC’98 Digest of Post-
´
deadline Papers, paginas QPD12-2, Optical So-
ciety of America, Washington, DC, 1998.
[WR2000] D.S. Bethune, W.P. Risk. An autocompensating
fiber-optic quantum cryptography system based
on polarization splitting of light. Journal Quantum
Electronics, 36(3):100, 2000.
[Mayers1998] D. Mayers. Unconditional security in quantum
cryptography. quant-ph/9802025, 1998.
[LC1999] H. Lo, H.F. Chau. Unconditional security of
quantum key distribution over arbitrary long dis-

86. 86
tances. Science, 283:2050-2056, 1999. quant-
ph/9803006.
[BBCAl1995] A. Barenco, C.H. Bennet, R. Cleve, D. P. DiVin-
cenzo, N. Margolus, P. Shor, T. Sleator, J. Smolin,
H. Weinfurter. Elementary gates for quantum
computation. Physical Review A, 52:3457-3467,
1995. quant-ph/9503016
[Div1998] D.P. Divincenzo. Quantum gates and circuits.
Proceedings of the Royal Society of London A,
454:261-276, 1998.
[BMPRV1999] P.O. Boykin, T. Mor, M. Pulver, V. Roychowdhury,
F. Vatan. On universal and fault-tolerant quantum
computing, 1999. quant-ph/9906054
[Knill1995] E. Knill. Approximating quantum circuits,
1995.quant-ph/9508006

87. 87
[Deutsch1989] D. Deutsch. Quantum computational networks.
Proceedings of the Royal Society London A,
425:73, 1989.
[Yao1993] A. C. Yao. Quantum circuit complexity. Pro-
ceedings of the 34th Annual IEEE Symposium
on Foundations of Computer Science, 352-361,
1993.
[Ben1980] P. Benioff. The computer as a physical system:
a microscopic quantum mechanical Hamiltonian
model of computer as represented by Turing ma-
chines. Journal of Statistical Physics, 22(5):563-
591, 1980.
[Deutsch1985] D. Deutsch. Quantum theory, the Church-Turing
principle and the universal quantum computer.

88. 88
Proceedings of the Royal Society of London A,
400:97, 1985.
[Toffoli1980] T. Toffoli. Reversible computing, Automata, Lan-
guages and Programming, Seventh Colloquium,
Lecture Notes in Computer Science vol. 84, eds.
J.W. de Bakker y J. van Leeuwen, Springer, New
York, 632-644, 1980.
[DJ1992] David Deutsch, Richard Jozsa. Rapid solution of
problems by quantum computation, Proceedings
of the Royal Society of London A, vol 439, 553-
558, 1992.
[Grover1996] Lov Grover. A fast quantum-mechanical algo-
rithm for database search. Proceedings of the
28th Annual ACM Symposium on Theory of
Computing, ACM, New York, 1996.

89. 89
[BBHT1998] Michel Boyer, Gilles Brassard, Peter Hoyer,
Alain Tapp. Tight bounds on quantum searching.
Forstchritte Der Physik , Special issue on quan-
tum computing and quantum cryptography, vol.
4, 820-831, 1998. quant-ph/9605034
[LL1993] A.K. Lenstra, H.W. Lenstra Jr., eds., The develop-
ment of the Number Field Sieve, Lecture Notes in
Mathematics, vol 1554, Springer, Berlin and New
York, 1993.
[DivS1995] D. P. DiVincenzo. Quantum Computation. Sci-
ence, 270:255, 1995. quant-ph/9503016
[CY1995] I.L. Chuang, Y. Yamamoto. Simple quantum com-
puter. Physical Review A, 52:3489-3496, 1995.
quant-ph/9505011

90. 90
[IY1994] A. Imagoglu, Y. Yamamoto. Turnstile device for
heralded single photons: Coulomb blockade of
electron and hole tunneling in quantum confined
p-i-n heterojunctions. Physical Review Letters,
72(2):220-13, 1994.
[KSCEP1994] P.G. Kwiat, A. M. Steinberg, R.Y. Chiao, P.H.
Eberhard, M.D. Petroff. Absolute efficiency and
time-response measurement of single-photon
detectors. Applied Optics. 33(10):1844-1853,
1994.
[WY1990] K. Watanabe, Y. Yamamoto. Limits on tradeoffs
between third-order optical nonlinearity, absorp-
tion loss and pulse duration in self-induced trans-
parency and real excitation. Physical Review A,
42(3):1699-702, 1990.

91. 91
[KMSW1999] P.G. Kwiat, J.R. Mitchell, P.D.D. Schwindt, A.G.
White. Grover’s search algorithm: an optical ap-
proach, 1999. quant-ph/9905086
[THLMK1995] Q.A. Turchette, C.J. Hood, W. Lange, H.
Mabuchi, H. J. Kimble. Measurement of condi-
tional phase shifts for quantum logic. Physical
Review Letters, 75:4710, 1995.
[TPhD1997] Q.A. Turchette. Quantum optics with single
atoms ans single photons. Ph.D. thesis, Califor-
nia Institute of Technology, Pasadena, California,
1997.
[CZ1995] J.I. Cirac, P. Zoller. Quantum computations with
cold trapped ions. Physical Review Letters,
74:4091, 1995.

92. 92
[WMILKM1998] D.J. Wineland, C. Monroe, W.M. Itano, D.
Leibfried, B.E. King, D.M. Meekhof. Experimen-
tal issues in coherent quantum-state manipula-
tion of trapped atomic ions. J. Res. Natl. Inst.
Stand. Tech., 103:259, 1998.
[MMKIW1995] C. Monroe, D.M. Meekhof, B.E. King, W.M. Itano,
D.J. Wineland. Demonstration of a fundamen-
tal quantum logic gate. Physical Review Letters,
75:4714, 1995.
[J1998] D. James. The theory of heating of the quan-
tum ground state of trapped ions, 1998. quant-
ph/9804048
[OK1996] M. B. Plenio, P.L. Knight. Realistic lower bounds
for the factorization time of large numbers on a

93. 93
quantum computer. Physical Review A, 53:2986-
2990, 1996.
[W1997] W. Warren. The usefulness of NMR quantum
computing. Science, 277(5332):1688, 1997.
[SC1999] R. Schack, C.M. Caves. Classical model for bulk-
ensemble NMR quantum computation. Physical
Review A, 60(6):4354-4362, 1999.
[BCJLPS1999] S.L. Braunstein, C.M. Caves, R. Jozsa, N. Lin-
den, S. Popescu, R. Schack. Separability of very
noisy mixed states and implications for NMR
quantum computing. Physical Review Letters,
83(5):1054-1057, 1999.
[Vid1999] G. Vidal. Entanglement of pure states for a single
copy. Physical Review Letters, 83(5):1046-1049,
1999.

94. 94
[KHSL1999] K. Zyczkowski, P. Horodecki, A. Sanpera, M.
Lewenstein. Volume of the set of separable
states. Physical Review A, 58(2):883-892, 1999.
[LP1999] N. Linden, S. Popescu. Good dynamics versus
bad kinematics. Is entaglement needed for quna-
tum computation?, 1999. quant-ph/9906008
[CFH1997] D.G. Cory, A.F. Fahmy, T.F. Havel. Ensemble
quantum computing by NMR sprectroscopy. Pro-
ceedings of the National Academy of Sciences
USA, 94:1634-1639, 1997.
[GC1997] N. Gershenfeld, I.L. Chuang. Bulk spin reso-
nance quantum computation. Science, 275:350,
1997.

95. 95
[CGK1998] I. L. Chuang, N. Gershenfeld, M. Kubinec. Exper-
imental implementarion of fast quantum search-
ing. Physical Review Letters, 18(15):3408-3411,
1998.
[VYSC1999] L. M. K. Vandersypen, C.S. Yannoni, M.H. Sher-
wood, I.L. Chuang. Realization of effective pure
states for bulk quantum computation. Physical
Review Letters, 83:3085-3088, 1999.
[CVZLL1998] I.L. Chuang, L.M.K. Vandersypen, X.L. Zhou,
D.W. Leung, S. Lloyd. Experimental realization
of a quantum algorithm. Nature, 393(6681):143-
146, 1998.
[CMPAl1998] D.G. Cory, W. Mass, M. Price, E. Knill, R.
Laflamme, W.H. Zurek, T.F. Havel, S.S. Somaroo.

96. 96
Experimental quantum error correction, 1998.
quant-ph/9802018
[STHAl1999] S. Somaroo, C.H. Tseng, T.F. Havel, R.
Laflamme, D.G. Cory. Quantum simulations on
a quantum computer. Physical Review Letters,
82:5381-5384, 1999.
[LVZAl1999] D.W. Leung, L.M.K. Vandersypen, X. Zhou, M.
Sherwood, C. Yannoni, M. Kubinec, I.L. Chuang.
Experimental realization of a two-bit phase
damping quantum code. Physical Review A,
60:1924, 1999.
[JM1998] J.A. Jones, M. Mosca. Implementation of a quan-
tum algorithm to solve Deutsch’s problem on a
nuclear magnetic resonance quantum computer,
1998. quant-ph/9802018

97. 97
[JMH1998] J.A. Jones, M. Mosca, R.H. Hansen. Implemen-
tation of a quantum search algorithm on a nucle-
ar magnetic resonance quantum computer. Na-
ture, 393(6683):344, 1998. quant-ph/9805069
[SW1949] C.W. Shannon, W. Weaver. The mathematical
theory of communication. University of Illinois
Press, Urbana, 1949.
[Sha1948] C.E. Shannon. A mathematical theory of commu-
nication. Bell System Technical Journal, 27:379-
423, 623-656, 1948.
[SN1996] B.W. Schumacher, M.A. Nielsen. Quantum data
processing and error correction. Physical Review
A, 54(4):2629, 1996. quant-ph/9604022