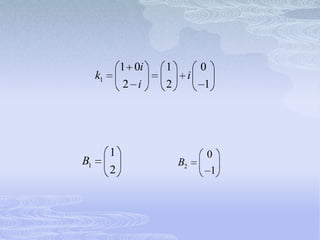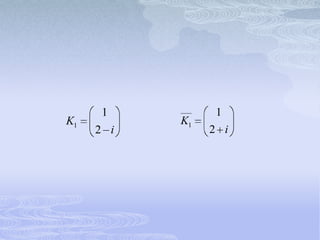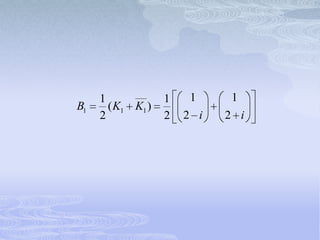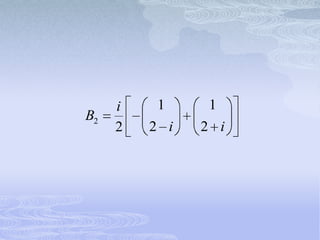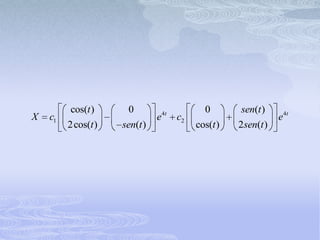El documento describe los sistemas lineales homogéneos de ecuaciones diferenciales de primer orden. Explica que la solución general de estos sistemas está dada por combinaciones lineales de vectores propios correspondientes a los valores propios de la matriz de coeficientes. También aborda casos como valores propios repetidos o complejos y cómo afectan las soluciones. Finalmente, presenta ejemplos para ilustrar los conceptos.













































![ ENTONCES
t
X1 [ B1 cos( t ) B2 sen( t )]e
t
(23)
X2 [ B2 cos( t ) B1sen( t )]e
SON SOLUCIONES LINEALMENTE
INDEPENDIENTES DE (2) EN ( , ) .](https://image.slidesharecdn.com/exposicionecuaciones-120327130423-phpapp02/85/Exposicion-ecuaciones-46-320.jpg)






































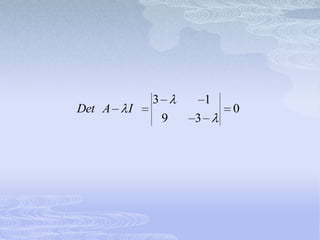


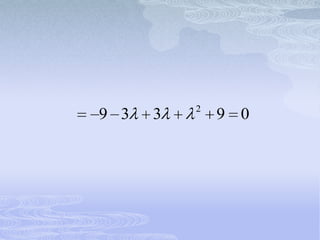











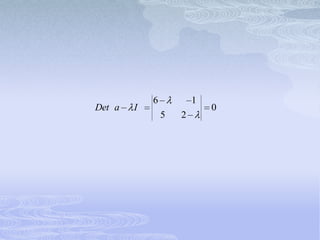
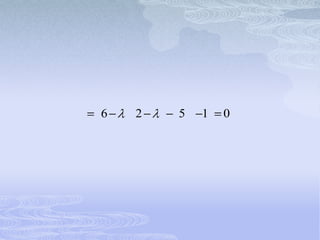


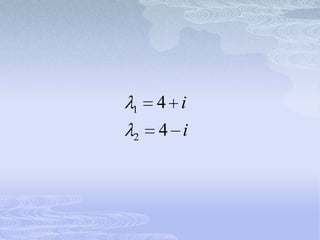

![ SI 1 4 i
6 4 i k1 k2 0
5k1 [2 4 i ]k2 0](https://image.slidesharecdn.com/exposicionecuaciones-120327130423-phpapp02/85/Exposicion-ecuaciones-106-320.jpg)