Este documento es un material de apoyo dirigido a los aspirantes de la facultad de ingeniería de la Universidad Nacional de la Patagonia San Juan Bosco, contiene información sobre las temáticas que se evalúan en el examen de ingreso y una variedad de ejemplos prácticos. Se abordan conceptos fundamentales de matemáticas, incluyendo números naturales, enteros, funciones, y distintos tipos de ecuaciones, como cuadráticas y polinómicas. El objetivo es desarrollar habilidades necesarias para el estudio de áreas básicas en ingeniería e informática.





![SIMBOLOS
N = {1, 2, 3, …} el conjunto de los números naturales
N0 = N ∪ {0} el conjunto { 0, 1, 2, 3, …}
N-
el conjunto { -1, -2, -3, -4, …}
Z = {…, -3, -2, -1, 0, 1, 2, 3,
…}
el conjunto de los números enteros
Q el conjunto de los números racionales
R el conjunto de los números reales
C el conjunto de los números complejos
x ∈ A x pertenece al conjunto A
x ∉ A x no pertenece al conjunto A
A ⊂ B el conjunto A está incluido en el conjunto B
A ⊄ B el conjunto A no está incluido en el conjunto B
A ∪ B conjunto A unión B, formado por los elementos que pertenecen
al conjunto A o al conjunto B
A ∩ B conjunto A intersección B, formado por los elementos que
pertenecen al conjunto A y al conjunto B
∅ conjunto vacío
= igual
≠ distinto
≅ es aproximadamente igual a
< es menor que
> es mayor que
≤ es menor o igual que
≥ es mayor o igual que
(a, b) el intervalo abierto de extremos a y b
[a, b] el intervalo cerrado de extremos a y b
(a, b] el intervalo semiabierto a izquierda o semicerrado a derecha, de
extremos a y b
[a, b) el intervalo semiabierto a derecha o semicerrado a izquierda, de
extremos a y b
∞ infinito](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-6-320.jpg)



































![Recta Real
Página 37
Frecuentemente trabajaremos con subconjuntos de números
reales, expresados de acuerdo con alguna relación de orden.
Así, por ejemplo, hablaremos de
En símbolos,
43421321
5quemenoresy
2quemayoresrealesnúmeros
}52/{ <<∈ xx R
“los números reales mayores que 2 y menores que 5”
o de
En símbolos,
321
321
3/2queiguales
omenores
realesnúmeros
}
2
3
/{ ≤∈ xx R
“los números reales menores o iguales que
2
3
”
Otras veces deberemos simbolizar expresiones tales como:
En símbolos,
350 < x < 400
“la cantidad x de ballenas que puede contabilizarse entre
Octubre y Noviembre se halla entre 350 y 400”
Estos subconjuntos de R se definen mediante intervalos.
Intervalo abiertoIntervalo abierto
(a , b)
Si a , b ∈∈ R y a < b, se define (a , b) = {x ∈∈ R / a < x < b}.
Gráficamente:
Intervalo cerradoIntervalo cerrado
[a , b]
Si a , b ∈∈ R y a ≤≤ b, se define [a , b] = {x ∈∈ R /a ≤≤ x ≤≤ b}.
Si a coincide con b ,
el intervalo cerrado es un único punto.
Gráficamente:
a b
ó
a b
a b
ó
a b](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-44-320.jpg)
![Curso de Apoyo en Matemática
Página 38
IntervalosIntervalos
semiabiertossemiabiertos
o semicerradoso semicerrados
Si a , b ∈∈ R y a < b se define:
(a , b] = {x ∈∈ R / a < x ≤≤ b }
[a , b) = {x ∈∈ R / a ≤≤ x < b }
Gráficamente:
(a , b] se representa como
[a , b) se representa como
En todos los casos, los números a y b se llaman extremo inferior y extremo superior del intervalo,
respectivamente.
Ejemplo:
Atención
Los símbolos - ∞ y + ∞
deben ser considerados con especial
cuidado, recordando que se usan
solamente por conveniencia de
notación y nunca como números
reales.
Estas definiciones se pueden generalizar, considerando a la
recta y a la semirrecta como intervalos, con sólo introducir los
símbolos - ∞ y + ∞.
Así, tenemos
en símbolos gráficamente
[ c , + ∞ ) = {x ∈ R / x ≥ c } →
( c , + ∞ ) = {x ∈ R / x > c } →
(- ∞ , d ] = {x ∈ R / x ≤ d } →
(- ∞ , d ) = {x ∈ R / x < d } →
(- ∞ , + ∞) = R →
a b
a b
Extremo inferior Extremo superior
a b
c
c
d
d
0](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-45-320.jpg)
![Recta Real
Página 39
Ejemplos:
[ - 2 , 2 ] = {x ∈ R / - 2 ≤ x ≤
2 }
→→
( - ∞ , - 1) = {x ∈ R / x < -1 } →→
( - 2 , e) →→
3
4
,
3
1
- →→
ACTIVIDADES DE APRENDIZAJE
1) Dados los siguientes subconjuntos de R:
a) A = { x / x ∈ N ∧ - 2 < x < 3 } b) B = { x / x ∈ Z ∧ - 2 < x < 3 }
c) C = { x / x ∈ Q ∧ - 2 < x < 3 } d) D = { x / x ∈ R ∧ - 2 < x < 3 }
Recuerda observar a qué conjunto
numérico pertenecen los elementos.
Por ejemplo, en el conjunto B
los elementos son números
“enteros” x tales que - 2 < x < 3.
i) Analizar los elementos que pertenecen a cada conjunto. ¿Es
posible determinar la cantidad de elementos?.
ii) Representar en la recta real, de ser posible, cada conjunto.
2)
En caso de que existan infinitos
números, el modo de indicarlos es
mediante la notación de intervalos.
a) ¿Cuáles son los números naturales comprendidos entre
-2 y 3 ?.
b) ¿Cuáles son los números enteros comprendidos entre
-2 y 3 ?.
c) ¿Cuáles son los números racionales comprendidos entre -2
y 3 ?.
d) ¿Cuáles son los números reales comprendidos entre
-2 y 3 ?.
3) Expresar mediante intervalos cada uno de los siguientes subconjuntos de R: el conjunto de los
números reales x que satisfacen:
a) x es mayor que 2 y menor que 6.
b) x es mayor o igual que -1.](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-46-320.jpg)
![Curso de Apoyo en Matemática
Página 40
c) x es menor que
3
2
.
d) x supera al menor número entero positivo.
e) x es menor que el mayor número par negativo.
f) x está comprendido entre los dos múltiplos positivos de 4 de un solo dígito.
4) Representar sobre la recta real los siguientes intervalos:
a) [2 , 5] b) {x/x ∈ R ∧ -3 < x <
3
4
}
c)
∞
2
1
;- d) {x/x ∈ R ∧ -1 ≤ x < 2,75 }
5) Determinar:
Recuerda que...
El símbolo ∪
representa la unión de conjuntos.
El símbolo ∩
representa la intersección de
conjuntos.
a) [-
4
1
, 2) ∪ [1 , + ∞) b) (-3 , -1) ∪ [
2
5
, 3)
c) (-3 , -1) ∩ [
2
5
, 3) d) [0 , 5 ) ∩ [
2
3
,
2
7
]
6) Hallar los valores de x que satisfacen las siguientes condiciones y representar los subconjuntos
de R correspondientes.
a) 0 < x ≤ 2 ∧ x ∈ [1 , 3) b) x > -1 ∧ x ∈ (2 , 5)
c) x ∈ [-4 , +∞) ∧ x < -2 d) x ∈ (-2 , 2) ∧ x ∈ [1 , +∞)
e) x ∈ (- ∞ , 3) ∧ x ∈ (-3 , +∞) f) -3 ≤ x < 1 ∧ x ∉ [0 , 2)
7) Dados los intervalos A = [-2 , 1) ; B = [-1 , + ∞) ; C = [-3 , 2,5) determinar:
a) (A ∩ B) ∩ C b) (A ∩ B) ∪ C
8) Sean A = [-2 , 6] ; B = (1 , 5] ; C = (-1, 3) calcula:
a) (A ∪ B) ∩ C b) (A ∩ B) ∪ C
9) Expresar en forma de intervalos la información dada en la introducción acerca de las Ballenas
Francas.](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-47-320.jpg)

![Curso de Apoyo en Matemática
Página 42
Ejemplo:
Recordemos que...
x ∈ R y x ≤ 2
es equivalente a
x ≤ 2 ∧ x ≥ - 2 .
Si representamos cada una de estas
desigualdades, la intersección de
ambos conjuntos es precisamente el
intervalo [- 2 , 2 ].
x ≤ 2 es equivalente a - 2 ≤ x ≤ 2 .
Por lo tanto, x ≤ 2 significa que x ∈ [- 2 , 2 ] .
Si representamos en la recta numérica obtenemos:
En general, - b ≤ x ≤ b es equivalente a
x ≥ - b ∧ x ≤ b
y representa la intersección
[- b , + ∞) ∩ (- ∞ , b] = [- b , b ]
Análogamente, x < b es equivalente a
- b < x < b
(o también x < b ∧ x > - b ).
La distancia de x al cero
debe ser mayor que 2 .
Una forma de encontrar los números reales x que verifican
x > 2 ,
es descartar de la recta real aquellos que verifican x ≤ 2 .
Así, se obtiene x > 2 o x < - 2 . Gráficamente,
Por la definición de intervalos,
x ∈ R y x > b
significa que
x ∈ (- ∞ , -b) ó x ∈ (b , + ∞) ,
es decir,
x > b
equivale a
x ∈ (- ∞ , -b) ∪ (b , + ∞) .
En general, si b ∈ R y b > 0 ,
x > b es equivalente a decir que x > b o x < -b .
Es decir, la distancia del x al cero debe ser mayor que b.
Gráficamente,
0-2 2
- 2 2
20
- 2 2
[ 2,2− ]
0 b-b
[-b, b]
0 b-b
(-b, b)
0-2 2
- 2 2
0
b-b](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-49-320.jpg)
![Recta Real
Página 43
x ∈ R y x ≥ b
significa que
x ∈ (- ∞ , -b] ∪ [b , + ∞)
Análogamente,
x ≥ b es equivalente a decir x ≥ b ó x ≤ - b.
Gráficamente,
Ejemplo:
x - a < b
significa que x está a menos de b
unidades respecto de a; mientras que
x - a > b
significa que x está a más de b
unidades de a.
En el caso general
x - a
mide la distancia entre x y a .
ACTIVIDADES DE APRENDIZAJE
10) Resolver y representar gráficamente. Expresar la solución, de ser posible, en forma de
intervalos.
Ejemplo:
x + 9 = 5
Solución:
x + 9 = 5 → x + 9 = 5 óx + 9 = -5
→ x = 5 – 9 ó x = -5 – 9
→ x = - 4 ó x = - 14
La solución en este caso es entonces
S = {-4, -14}.
Gráficamente:
a) x =
2
3
b) x - 5 = 2
c) x ≥ 3 d) x ≤ 5
11) Expresar las afirmaciones siguientes, si es posible, como intervalos:
a. x está a menos de 5 unidades de 3
b. y está a lo sumo 4 unidades de 7
c. t está a una distancia de 3 unidades de 5
d. x está al menos a 4 unidades de - 5
e. x es menor que 4 y mayor que - 4
0 b-b
-14 - 4 0](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-50-320.jpg)

![Recta Real
Página 45
b) 4
2
1
>
+x
Aplicando propiedades Despejando:
2
1+x
> 4
2
1+x
> 4
2
1+x
. 2 > 4 . 2 x + 1 > 4 . 2
x + 1 > 8 x + 1 > 8
x + 1 + (- 1) > 8 + (- 1) x > 8 - 1
x > 7 x > 7
Solución: S = ( 7 , + ∞ )
Representación gráfica:
c) x + y ≥ 24
En este caso tenemos una inecuación lineal con dos incógnitas, que se verifica para infinitas parejas
de números.
Verificación:
Ejemplo:
0 + 24 ≥ 24 x = 0 ; y = 24
2 + 23 ≥ 24 x = 2 ; y = 23
-3 + 30 ≥ 24 x = -3 ; y = 30
2
1
+
3
71
≥ 24 x =
2
1
; y =
3
71
1 + 100 ≥ 24 x = 1 ; y = 100
d) -2 x + 1 ≤ x – 3
Aplicando propiedades: Despejando:
-2 x + 1 ≤ x - 3 - 2 x + 1 ≤ x - 3
-2 x + 1 + (-x ) ≤ x - 3 + (- x ) - 2 x - x ≤ - 3 - 1
[-2 x + (-x ) ] + 1 ≤ [ x + (- x ) ] - 3
-3 x + [ 1 + (-1 ) ] ≤ - 3 + (-1 )
-3 x ≤ - 4
- 3 x ≤ - 4
-
3
1
. (-3) x ≥ -
3
1
.(-4) x ≥ - 4 : (- 3)
75 96 8... 1110 ...](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-52-320.jpg)
![Curso de Apoyo en Matemática
Página 46
x ≥
3
4
x ≥
3
4
Solución: S = [
3
4
, + ∞ )
Representación gráfica:
Las inecuaciones permiten resolver problemas.
Ejemplo:
Una furgoneta pesa 875 kg. La diferencia entre el peso de la furgoneta vacía y el peso de la carga
que lleve no debe ser inferior que 415 kg. Si hay que cargar cuatro cajones iguales, ¿cuánto puede
pesar, como máximo, cada uno de ellos para poder llevarlos en esa furgoneta?
En primer lugar, traducimos el
enunciado al lenguaje simbólico
Sea x el peso de cada cajón y planteamos la siguiente
inecuación:
Peso de la furgoneta - peso de 4 cajones no es menor que 415 kg
875 - 4 . x ≥ 415
Debemos resolver entonces la inecuación
Pasos de resolución: 875 – 4x ≥ 415
Restamos 875 a ambos miembros
de la desigualdad
→ - 4 . x ≥ 415 - 875
Hacemos el cálculo en el segundo
miembro
→ - 4 . x ≥ - 460
Para despejar x , multiplicamos
a ambos miembros por - ¼.
Recordemos que cuando
multiplicamos por un número
negativo, debemos cambiar el sentido
de la desigualdad
→ x ≤ ( )460
4
1
−⋅
−
Hacemos el cálculo → x ≤ 115
Esto significa que el peso de cada cajón no podrá superar los 115 kg. Además, como se trata
de un peso, x > 0. Entonces, la solución está formada por todos los números reales
pertenecientes al intervalo (0 , 115]. Graficamos la solución en la recta real:
0-1 1
3
4
32
0 115](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-53-320.jpg)

![Curso de Apoyo en Matemática
Página 48
17) El perímetro de un cuadrado no supera el perímetro del rectángulo de la figura. ¿Qué se puede
asegurar acerca de la superficie S del cuadrado ?.
18) Un padre y su hijo se llevan 22 años. Determinar en qué período de sus vidas, la edad del padre
excede en más de 6 años al doble de la edad del hijo.
19) Un coche se desplaza por una carretera a una velocidad comprendida entre 100 Km/h y 150
Km/h. ¿Entre qué valores oscila la distancia del coche al punto de partida al cabo de 3 horas?.
20) Una fábrica paga a sus viajantes $10 por artículo vendido más una cantidad fija de $500.Otra
fábrica de la competencia paga $15 por artículo y $300 fijas. ¿Cuántos artículos debe vender el
viajante de la competencia para ganar más dinero que el primero?.
21) Sean A = {x/x ∈ R ∧ x + 1 < 4 } y B = (- ∞ ,
2
3
] ∪ [3 , + ∞) . Determinar A ∩ B
22) Determinar:
{x / x ∈ R ∧ 2 x - 4 > 0 } ∩ {x / x ∈ R ∧ 3 - x ≥ 0 }
23) Hallar y representar en la recta los números reales que verifican:
a) x - 4 > 2 b) x + 2 ≤ 3 c) 4 - x > 0
d) 0 < x + 3 < 1 e) 0 < x - 3 <
4
1
f) 12 - 4 x > 3
g) 4 x - 3 ≤ 5 h) - 3 x + 6 < 2 i) 1 + 2 x ≥
2
1
j) 3 - x - 5 ≥ 0 k) - 2 x + 1 + 8 < 0](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-55-320.jpg)

![Función Lineal y Ecuación de la Recta
Página 51
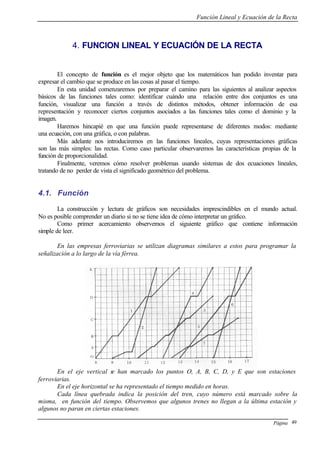
Eje de OrdenadasEje de Ordenadas En el eje vertical se ubica la variable dependiente y recibe
el nombre de eje de ordenadas o eje y.
Gráficamente
Al representar una función y = f (x) en un sistema de
coordenadas cartesiano, sobre el eje de abscisas se ubica la
variable independiente x, mientras que sobre el eje de
ordenadas se ubica la variable dependiente y.
DominioDominio
Al conjunto formado por todos los valores que toma la
variable independiente x lo denominamos dominio de la
función y lo denotamos Dom f.
En el gráfico anterior podemos leer
Dom f = [ a , b ]
ImagenImagen
Al conjunto formado por todos los valores que toma la
variable dependiente y tales que y = f (x) para algún
x ∈∈ A, lo denominamos imagen de la función y lo denotamos
Im f.
En el gráfico anterior podemos leer
Im f = [ c , d ]
Para una función f : A → B , se tiene que A = Dom f e Im f ⊆ B
No todo lo que parece es una función. Es importante aprender a reconocer cuándo una relación entre
dos conjuntos es o no una función.
Analicemos los siguientes gráficos, que muestran relaciones desde un conjunto A hacia un conjunto
B, donde A = [ 1 , 5 ] y B = [ 0 , 5 ]
Gráfico 1
El Gráfico 1 no representa una función pues hay elementos del
dominio que tienen más de una imagen.
Ejemplo:
f (3) = 2 y f (3) = 4.
a b
c
d
y eje de ordenadas
eje de abscisas
x42
3
2
1 3 5
1
4
5
y](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-58-320.jpg)
![Curso de Apoyo en Matemática
Página 52
Gráfico 2
El Gráfico 2 corresponde a una función puesto que todos los
elementos de A tienen una única imagen en B.
En este caso podemos observar que
Dom f = [ 1 , 5 ] e Im f = [ 0 , 4 ]
Gráfico 3
El Gráfico 3 no representa una función pues hay elementos del
conjunto A que no tienen imagen.
Por ejemplo, el punto (3,1) se ha marcado con un pequeño
círculo vacío para indicar que f (3) 1. Por otro lado, los
elementos que pertenecen al intervalo (4,5] no poseen imagen.
Mayor dominio deMayor dominio de
defindefiniiciónción
Cuando la función viene dada por una fórmula del tipo
y = f (x), el mayor dominio de definición es el conjunto de los
valores de x para los cuales se puede calcular f (x).
Para pensar...
Observemos que...
claramente es posible calcular 2 x
para cualquier número real x.
Luego, Dom f = R
a) Si f (x) = 2x,
¿para qué valores de x es posible calcular 2x ?.
Observemos que...
como la división por 0 no está
definida debe ser x - 1 ≠ 0 ,
o sea x ≠ 1.
Luego, Domf = R - {1}
b) Si
1
2
)(
−
=
x
xf ,
¿es siempre posible calcular este cociente?.
y
42
3
2
1 3 5
1
4
5
x
42
3
2
1 3 5
1
4
5
y
x](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-59-320.jpg)
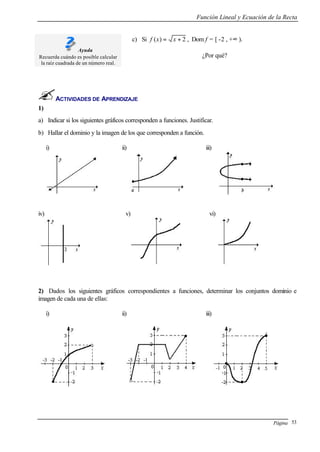
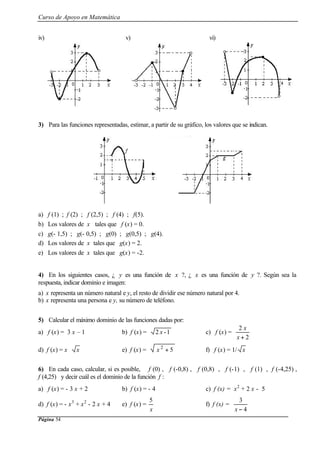

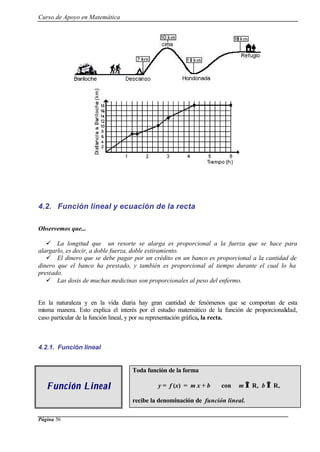

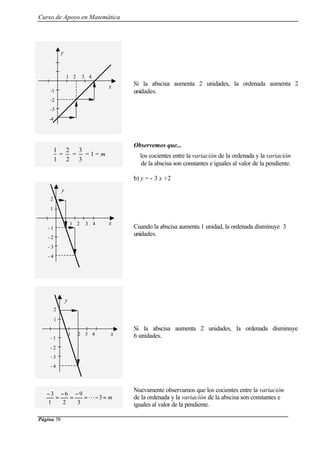
























![Curso de Apoyo en Matemática
Página 90
Comprueba efectuando la gráfica
correspondiente.
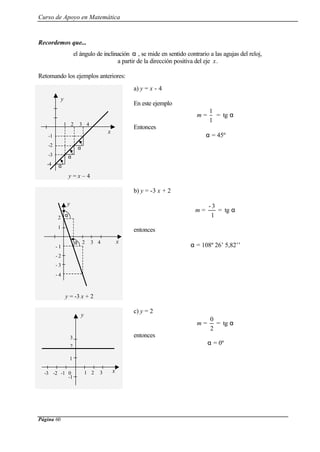
Ejemplo:
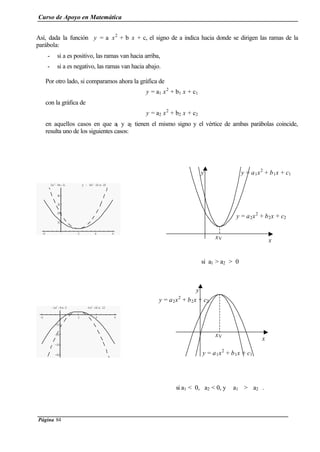
La función y = - x2
- 2 x - 3 , no tiene raíces reales.
Las coordenadas del vértice son :
xV =
a2
b-
=
1)(-2
2)(--
= - 1 e yV = - (-1)2
- 2 (-1) - 3 = - 2.
Para pensar….
Si no recuerdas el
método de completar cuadrados
es conveniente que
estudies nuevamente este tema
contenido en la unidad anterior.
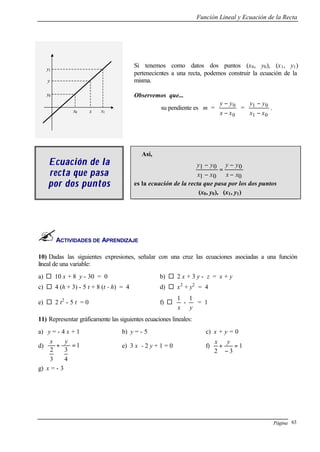
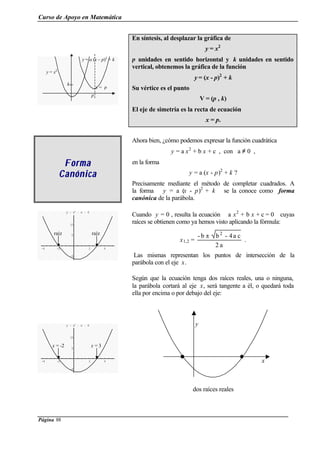
Considera la función y = 3x2
- 2 x – 1. Completando
cuadrados resulta y = 3 (x -
3
1
)2
-
3
4
.
Grafica la función y responde:
ü ¿ Hacia dónde está abierta la parábola ?
ü ¿ Cuáles son las coordenadas del vértice ?
ü ¿ Cuál es el eje de simetría ?
ü ¿ Cuáles son los puntos de intersección de la parábola con
los ejes x e y ?
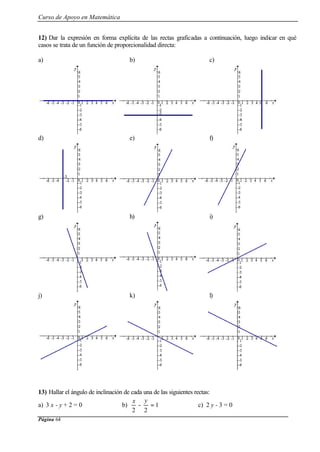
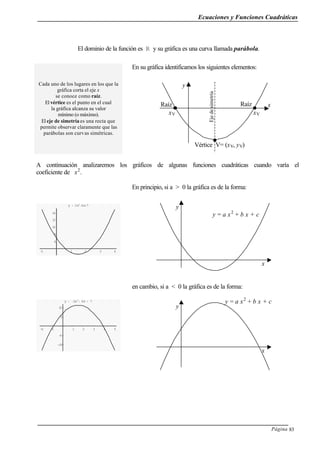
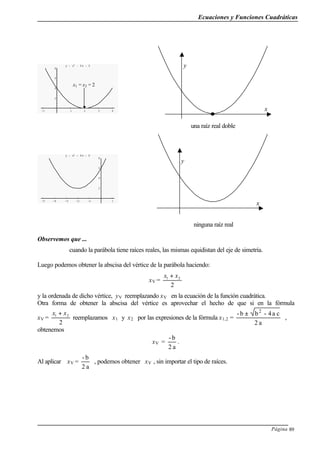
Ejemplo:
Hallaremos la expresión de la función cuadrática graficada.
-5 -4 -3 -2 -1 1
1
2
3
4
5
6
• reemplazamos las coordenadas del vértice en la forma canónica y = a [x - (- 2)] 2
+ 1
• Reemplazamos x e y por las coordenadas del punto P: 3 = a (- 1 + 2)2
+ 1
• Obtenemos: a = 2
• Sustituimos en la ecuación y = a [x - (-2)] 2
+ 1 el valor de a y obtenemos la expresión de
la función:
y = 2 (x + 2)2
+ 1
V
P](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-97-320.jpg)
























































![Curso de Apoyo en Matemática
Página 152
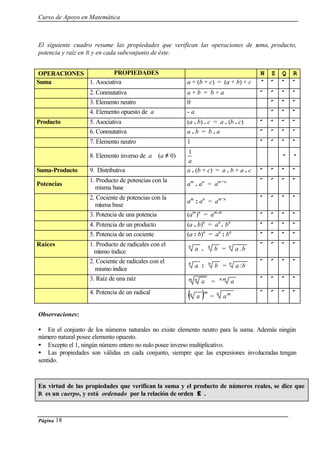
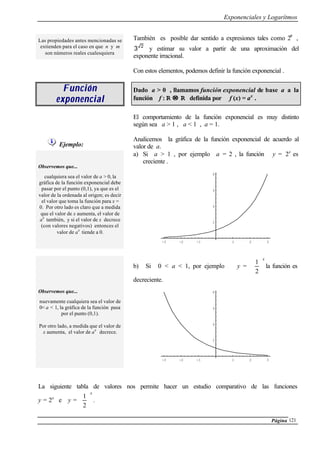
23) Escribir todos los ángulos α (comprendidos entre 0 y 360) cuyo coseno valga -0.5.
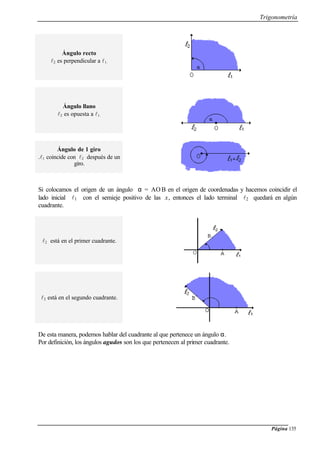
24) ¿Para qué valores de α ∈ [0 , 2π] el seno y el coseno coinciden?
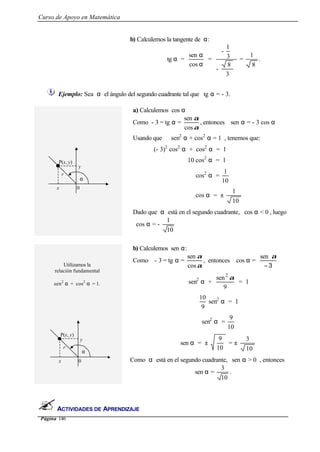
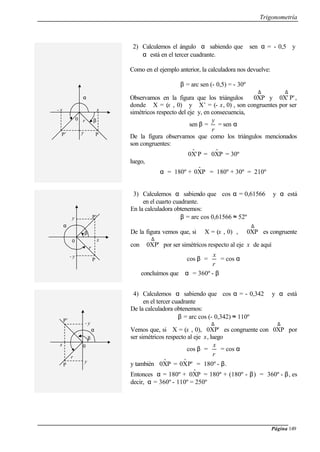
25) Resolver los siguientes triángulos:
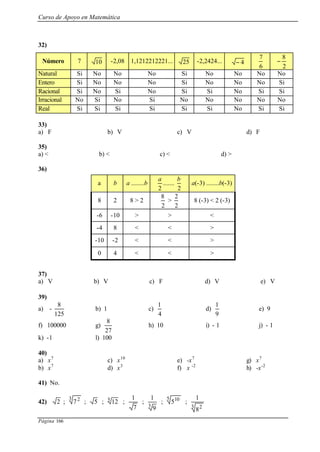
a) a = 5 cm , β = 30º , α = 90º
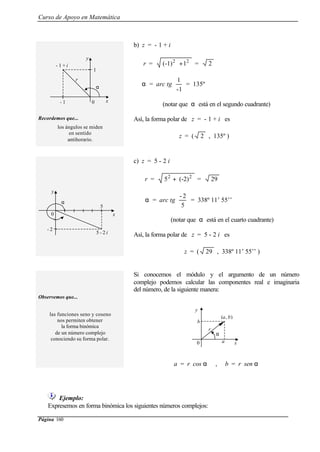
b) b = 2 cm , c = 5 cm , α = 90º
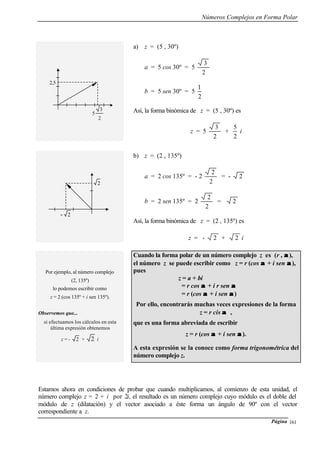
c) b = 82 cm , α = 90º , γ = 57º
26) Cuando el ángulo de elevación del sol sobre el horizonte es de 30º, una torre proyecta una
sombra de 75 m. Calcular su altura.
27) ¿Cuán larga es la sombra que arroja un mástil de 11 m de altura cuando el sol tiene una
elevación de 20º?.
28) El hilo que sujeta un barrilete mide 250 m y forma un ángulo de 32º con la vertical. Hallar la
altura a que se halla si se supone que el hilo está en línea recta.
29) Un automóvil asciende una cuesta que tiene una inclinación de 22º. Si viaja a una velocidad de
60 km/h, ¿cuántos metros varía su altura sobre el nivel del mar en 15 minutos?.
30) Se piensa construir una pista de aviación y debido a la orientación elegida se ve que al final de
la misma quedará una arboleda de 25 m de altura. ¿A qué distancia mínima de la arboleda debe
terminar la pista si el ángulo de despegue de los aviones es de 16º?.
31) Cuando se apoya una escalera de 3 m de largo en una de las paredes de un pasillo, llega a una
altura de 2,50 m. Si se la inclina sobre la otra pared llega a 2 m de altura. Averiguar el ancho del
pasillo.
32) Un carpintero desea construir una escuadra de madera y necesita que uno de los ángulos sea de
30º. Desea saber las relaciones que deben guardar los lados entre sí.
33) Los lados paralelos de un trapecio miden 6 cm y 8 cm, y los otros dos miden 3 cm. Hallar las
longitudes de sus diagonales y su área.
34) El frente de un terreno da sobre una diagonal y tiene las dimensiones que se indican en el
esquema. Calcular los metros que tiene el frente y el área que ocupa.
35) Se quiere saber cuántos metros de alambrado son necesarios para cerrar el terreno sombreado de
la figura:](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-159-320.jpg)















![Soluciones de los Ejercicios de Aplicación
Página165
2)
a) 1 y 2
b) -1, 0, 1 y 2
c) (-2 , 3) ∩ Q
d) (-2 , 3)
3)
a) (2, 6) b) [-1 , + ∞) c) (- ∞ ,
3
2
)
d) (1 , + ∞) e) (- ∞ , -2) f) (4, 8)
4)
a) b)
c) d)
5)
a)
∞+− ,
4
1 b) (-3 , -1) ∪
3,
2
5 c) Ø d)
5,
2
3
6)
a) [ 1 , 2 ] b) ( 2 , 5 ) c) [- 4 , -2 )
d) [ 1 , 2 ) e) ( -3 , 3 ) f) [ -3 , 0 )
7)
a) [-1 , 1) b) [-3 , 2,5)
8)
a) ( -1 , 3 ) b) ( -1 , 5 ]
9)
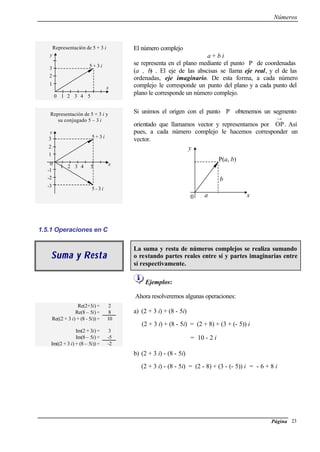
a) x = -
2
3
ó x =
2
3 b) x = 3 ó x = 7
c) (-∞ , -3] ∪ [3 , ∞) d) [-5 , 5]](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-178-320.jpg)
![Curso de Apoyo en Matemática
Página 166
10)
a) x ∈ (-2 , 8) b) y ∈ [3 , 11] c) t = 2 ó t = 8
d) x ∈ (-∞ , -9] ∪ [-1 , ∞) e) x ∈ (-4 , 4)
11)
Si denotamos con p al peso de la ballena, y con x la cantidad de ballenas que se concentran entre
octubre y noviembre, resulta
p ∈ [ 30 , 35 ] x ∈ [ 350 , 400 ]
12)
a)
∞−
4
7
, b)
∞−
4
1
-,
c) (- ∞ , 3 )
d)
∞,
2
7 e) (- ∞ , -1 ) f) [10, + ∞ )
g) (- ∞ , 6] h)
∞−
3
1
,
i) (5 , + ∞ )
j) (- ∞ , - 2 ] k) (4 , + ∞ ) l) (6 , + ∞ )
m) (- ∞ , 1 ) n) ( )∞+,2
13) Falso
14) Cualquier número mayor que 20.
15) 4
16) p ≥ 28
17) S ≤ 16
18) Cuando la edad del hijo es menor que 16 y la del padre menor que 38.
19) Entre 300 km y 450 km.
20) Debe vender más de 40 artículos.
21)
∞−
2
3
,
22) (2 , 3]](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-179-320.jpg)
![Soluciones de los Ejercicios de Aplicación
Página167
23)
a) (- ∞ , 2 ) ∪ ( 6, + ∞ ) b) [-5 , 1]
c) R - {4} d) (- 4 , - 3 ) ∪ ( - 3, - 2 )
e)
4
13
,33,
4
11
∪
f) ,
4
15
4
9
,-
∞+∪
∞
g)
− 2,
2
1 h)
3
8
,
3
4
i) ,
4
1
4
3
,-
∞+−∪
−∞
j) (- ∞ , -2 ] ∪ [ 8 , + ∞ )
k) (- ∞ , -5) ∪ (3 , + ∞ )
UNIDAD 4: FUNCIÓN LINEAL Y ECUACIÓN DE LA RECTA
1) a).i) Si ii) Si iii) No
iv) No v) Si vi) Si
b) i) Dom f = R ii) Dom f = [a , +∞) iii) --------
Im f = RIm f = [f (a) , +∞)
iv) -------- v) Dom f = R vi) Dom f = (0 , +∞)
Im f = R Im f = (0 , +∞)
2) i) Dom f = [-2 , 3) ii) Dom f = (-3 , 4] iii) Dom f = [0 , 5]
Im f = [-2 , 2) Im f = (-2 , 3] Im f = [-2 , 3]
iv) Dom f = (-3 , 3) v) Dom f = (-3 , 4) vi) Dom f = (-3 , 4)
Im f = [-2 , 3] Im f = (-3 , 3) Im f = (-2 , 3)
3)
a) f (1) = 2 ; f (2) = 3 ; f (2,5) = 1,5 ; f (4) = -1 ; f (5) = 1,5](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-180-320.jpg)
![Curso de Apoyo en Matemática
Página 168
b) x = 3 ; x = 4,75
c) g(- 1,5) = -1 ; g(- 0,5) = 1 ; g(0) = 1,5 ; g(0,5) = 1,75 ; g(4) = 2,5
d) x ∈ [1 , 3]
e) x ∈ (-∞ , -2]
4)
a) y es función de x. El dominio es N y la imagen es {0, 1, 2, 3}.
x no es función de y
b) y no es función de x.
x es función de y. El dominio es el conjunto formado por los números telefónicos y la imagen
es el conjunto formado por los abonados telefónicos.
5)
a) Dom f = R
b) Dom f = [
2
1
, +∞ ]
c) Dom f = R - {-2}
d) Dom f = [0 , +∞)
e) Dom f = R
f) Dom f = (0 , +∞)
6)
g) f (0) = 2 f (-0,8) = 4,4 f (0,8) = -0,4 f (-1) = 5
f (1) = -1 f (-4,25) = 14,75 f (4,25) = -10,75 Dom f = R
h) f (0) = f (-0,8) = f (0,8) = f (-1) = f (1) = f (-4,25) = f (4,25) = - 4 Dom f = R
i) f (0) = -5 f (-0,8) = -5,96 f (0,8) = -2,76 f (-1) = -6
f (1) = -2 f (-4,25) = 4,562 f (4,25) = 21,562 Dom f = R
j) f (0) = 4 f (-0,8) = 6,752 f (0,8) = 2,528 f (-1) = 8
f (1) = 2 f (-4,25) = 107,328 f (4,25) = -63,203 Dom f = R
k) f (0) = no existe f (-0,8) = -6,25 f (0,8) = 6,25 f (-1) = -5
f (1) = 5 f (-4,25) = -1,176 f (4,25) = 1,176 Dom f = R - {0}
l) f (0) = -
4
3
f (-0,8) = -0,625 f (0,8) = -0,937 f (-1) = -
5
3
f (1) = - 1 f (-4,25) = -
∩
36,0 f (4,25) = 12 Dom f = R - {- 4}
7)
a) Si b) Si c) i) diario opositor ii) diario oficialista.](https://image.slidesharecdn.com/cursodeapoyoenmatematica-130719124740-phpapp02/85/curso-de-apoyo-en-matematica-181-320.jpg)