Este documento describe los modelos de estimación para sistemas de posicionamiento vía satélite como GPS, GLONASS y Galileo. Explica el principio de posicionamiento circular, donde las distancias entre satélites y receptor permiten determinar la posición del receptor. Luego detalla las variables y fuentes de error de los modelos, y los métodos para resolver el sistema de ecuaciones como Bancroft, linealización y filtrado de Kalman. Finalmente, introduce el posicionamiento hiperbólico y sus componentes.

1. Modelos de estimaci´on para sistemas de
posicionamiento
Javier Garc´ıa-Blanch
24 de junio de 2004
1

2. ´Indice General
1 Introducci´on a la navegaci´on v´ıa sat´elite 4
1.1 El Sistema de Posicionamiento Global - GPS . . . . . . . . . 4
1.2 GLONASS . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3 GALILEO EGNOS . . . . . . . . . . . . . . . . . . . . . . . 6
2 Principio de posicionamiento circular 7
3 Modelo de estimaci´on para posicionamiento v´ıa sat´elite 8
3.1 Aplicaci´on del posicionamiento circular . . . . . . . . . . . . . 8
3.2 C´alculo de las posiciones de los sat´elites . . . . . . . . . . . . 10
3.2.1 Posiciones de los sat´elites de GPS . . . . . . . . . . . 11
3.2.2 Posiciones de los sat´elites GLONASS . . . . . . . . . . 13
3.2.3 Conversi´on PZ-90 a WGS84 . . . . . . . . . . . . . . . 13
3.3 Modelizaci´on de las fuentes de error . . . . . . . . . . . . . . 14
3.3.1 Retardo ionosf´erico . . . . . . . . . . . . . . . . . . . . 14
3.3.2 Retardo troposf´erico . . . . . . . . . . . . . . . . . . . 14
3.4 Efectos relativ´ısticos . . . . . . . . . . . . . . . . . . . . . . . 16
3.5 Efecto multicamino . . . . . . . . . . . . . . . . . . . . . . . . 16
4 Soluci´on al sistema de ecuaciones que define la navegaci´on
v´ıa sat´elite 16
4.1 M´etodo de Bancroft . . . . . . . . . . . . . . . . . . . . . . . 17
4.2 Soluci´on mediante linealizaci´on por desarrollos de Taylor . . . 18
4.3 Soluci´on iterativa . . . . . . . . . . . . . . . . . . . . . . . . . 19
4.3.1 Filtrado de Kalman . . . . . . . . . . . . . . . . . . . 19
4.3.2 T´ecnicas de suavizado (o smoothing) . . . . . . . . . . 22
4.4 Medidas de precisi´on . . . . . . . . . . . . . . . . . . . . . . . 22
5 Programa de Matlab 23
6 Introducci´on al posicionamiento hiperb´olico 27
7 Modelo de estimaci´on para posicionamiento hiperb´olico 28
7.1 Variables del modelo . . . . . . . . . . . . . . . . . . . . . . . 28
7.2 Fuentes de error . . . . . . . . . . . . . . . . . . . . . . . . . 29
8 Disposici´on geom´etrica de los receptores 30
9 Soluci´on al sistema de ecuaciones que define el posicionamien-
to hiperb´olico 32
9.1 Introducci´on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
9.2 El m´etodo de Bancroft aplicado al sistema hiperb´olico . . . . 33
9.3 Soluci´on mediante linealizaci´on por desarrollos de Taylor . . . 34
2

3. 9.4 El filtro de Kalman y el posicionamiento hiperb´olico . . . . . 36
10 Inicializaci´on del sistema 38
10.1 Introducci´on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
10.2 Posici´on real de los puntos de referencia . . . . . . . . . . . . 39
10.3 Ajuste de la posici´on real de los puntos de referencia . . . . . 39
10.4 Sincronizaci´on de los relojes de los receptores . . . . . . . . . 41
10.5 Resoluci´on de la inicializaci´on por partes . . . . . . . . . . . . 43
10.6 Resoluci´on conjunta de la inicializaci´on . . . . . . . . . . . . . 44
10.7 Supervisi´on de receptores no est´aticos . . . . . . . . . . . . . 46
3

4. 1 Introducci´on a la navegaci´on v´ıa sat´elite
Existen en la actualidad distintos sistemas de navegaci´on v´ıa sat´elite, cuyo
funcionamiento se basa en la transmisi´on de se˜nales en radio frecuencia
desde un conjunto de sat´elites. El usuario del sistema de navegaci´on utiliza
un sistema receptor capaz de estimar la posici´on del mismo a partir de las
se˜nales emitidas por los sat´elites.
En una primera clasificaci´on es posible distinguir entre dos tipos de sis-
temas: sistemas suficientes y sistemas de aumentaci´on o apoyo. Un sistema
suficiente es aquel con el que se puede calcular una posici´on. Ejemplos de es-
tos sistemas son el Sistema de Posicionamiento Global (GPS) americano, [1],
el Sistema en ´Orbita GLobal para la Navegaci´on v´ıa Sat´elite (GLONASS)
ruso, [2], y el sistema europeo GALILEO, [3]. Un sistema de aumentaci´on en
cambio es aquel que se utiliza junto con uno suficiente con el fin de obtener
una mayor precisi´on en la posici´on. Ejemplos de estos sistemas son el eu-
ropeo EGNOS, [4], el americano WAAS, [5] y el japon´es MSAS, [6]. China
tambi´en est´a desarrollando actividades en este campo [7].
1.1 El Sistema de Posicionamiento Global - GPS
El GPS comenz´o a desarrollarse en 1973 en el Departamento de Defensa
de Estados Unidos, fundamentalmente para aplicaciones militares. Sin em-
bargo, hoy en d´ıa se utiliza a nivel internacional en numerosas aplicaciones
civiles: aviaci´on comercial, topograf´ıa, agricultura, etc..
El GPS est´a constituido por 3 segmentos principales: el segmento es-
pacial, el segmento de control, y el segmento de usuario, que se detallan a
continuaci´on.
La configuraci´on original del segmento espacial se estableci´o en 24 sat´elites
situados sobre 4 planos orbitales (6 por plano). Esta capacidad se consigui´o
en julio de 1993 [10]. En la actualidad, debido tanto al reemplazamiento de
sat´elites que van quedado obsoletos como a diversas revisiones del sistema, el
n´umero de sat´elites orbitando es 32 [11]. Los sat´elites completan una vuelta
aproximadamente cada 12 horas. La siguiente gr´afica 1 muestra el segmento
espacial del GPS.
El segmento de control est´a formado por un conjunto de estaciones de
seguimiento distribuidas por toda la esfera terrestre. Su funci´on principal es
supervisar las ´orbitas y el estado de los sat´elites. Una parte de esta super-
visi´on consiste en la actualizaci´on de los datos de efemeris y almanaque. Los
sat´elites codifican y env´ıan estos datos en sus se˜nales para que los receptores
puedan determinar las posiciones de los sat´elites.
4

5. Figura 1: Constelaci´on de GPS
El segmento de usuario est´a formado por todos los sistemas receptores de
GPS. ´Estos pueden ser tanto receptores comerciales como militares. Pode-
mos citar a modo de ejemplo los receptores que forman parte del sistema de
navegaci´on de un autom´ovil o una red de receptores para la medici´on del
desplazamiento de placas tect´onicas.
1.2 GLONASS
El sistema GLONASS fue dise˜nado y puesto en funcionamiento por la an-
tigua Uni´on Sovi´etica. En la actualidad su mantenimiento est´a a cargo de
Rusia. Su segmento espacial fue dise˜nado para contener 24 sat´elites situa-
dos sobre 3 planos orbitales (8 por plano) [9]. Esta capacidad no ha podido
desarrollarse completamente debido a los problemas econ´omicos por los que
atraviesa Rusia. En la actualidad hay 10 sat´elites en ´orbita [12], dos de
los cuales fueron lanzados en los ´ultimos meses. Un sat´elite de GLONASS
completa su ´orbita en 8
17 de d´ıa.
Debido a sus restricciones de capacidad, hoy en d´ıa s´olo es posible utilizar
GLONASS de manera aut´onoma en algunas regiones de Rusia. H. Contr-
eras, en [8], expone los beneficios de combinar GLONASS con GPS para
mediciones topogr´aficas en minas de cobre. Debido a la forma de las minas
de cobre, en muchos puntos el receptor no puede adquirir la se˜nal de sufi-
5

6. cientes sat´elites de GPS. Sin embargo, al utilizar adem´as las se˜nales de los
sat´elites GLONASS visibles es posible realizar una estimaci´on satisfactoria
de la posici´on. Esta combinaci´on mejora por tanto la integridad de la posi-
ci´on. De todas formas, esto no quiere decir que con la combinaci´on anterior
se obtenga en general una mejora sustancial en la precisi´on, puesto que en
condiciones normales (6-7 sat´elites de GPS visibles), suele ser parecida para
ambos casos como ilustra la gr´afica 2.
2400 2450 2500 2550 2600 2650 2700 2750
−4
−2
0
2
4
6
8
10
12
GPS+Glonass
GPS
Error en el Calculo de la posicion GPS+GLONASS
Metros
Epocas
Figura 2: Combinaci´on de GPS y GLONASS
1.3 GALILEO EGNOS
La Agencia Espacial Europea (ESA) desarrolla en la actualidad el sistema
GALILEO que contar´a con 30 sat´elites distribu´ıdos en 3 planos orbitales.
El sistema entrar´a en funcionamiento a lo largo del 2008.
El sistema EGNOS, igualmente desarrollado por la ESA, est´a formado
por 3 sat´elites geoestacionarios que orbitan la tierra sobre Europa y env´ıan
datos sobre el estado de la atm´osfera. Estos datos sirven para que los usuar-
ios europeos de GPS alcancen una mayor precisi´on en la estimaci´on de la
posici´on.
6

7. 2 Principio de posicionamiento circular
Los sistemas de navegaci´on v´ıa sat´elite basan su funcionamiento en el prin-
cipio de posicionamiento circular, que utiliza el conocimiento de tiempos
absolutos de propagaci´on de varias se˜nales ∆ti entre un conjunto de pun-
tos de referencia, {xS1, xS2, xS3, ..., xSn} (las posiciones de los sat´elites),
y la posici´on desconocida xr del receptor, siendo xSi = (xSi, ySi, zSi), y
xr = (xr, yr, zr)). A partir de estos tiempos de propagaci´on ∆ti es posible
determinar la distancia eucl´ıdea o rango r entre emisor y receptor, ya que la
velocidad de propagaci´on de las se˜nales de radio es una constante conocida
c.
ri = c · ∆ti (1)
Asimismo, es bien sabido que una distancia eucl´ıdea corresponde a
ri = (xr − xSi)2 + (yr − ySi)2 + (zr − zSi)2 −→ ri = xr − xSi ,
y a partir de ah´ı se obtiene el siguiente sistema de ecuaciones
r1 = xr − xS1
r2 = xr − xS2
· · ·
ri = xr − xSi
· · ·
rn = xr − xSn . (2)
Cada una de estas ecuaciones corresponde en R2 a la descripci´on de un
c´ırculo de centro la posici´on xSi, de referencia conocida, y radio la distancia
ri medida entre los dos puntos. Esto significa que la posici´on xr del receptor
a determinar se encuentra sobre la circunferencia de centro xSi y radio ri.
La consideraci´on de una segunda ecuaci´on reduce la incertidumbre a los dos
puntos en los que la primera circunferencia se cortar´ıa con una segunda de
centro xSi+1 y radio ri+1. Una tercera circunferencia resolver´ıa la inc´ognita.
La representaci´on gr´afica corresponde a 3.
En R3 el sistema de ecuaciones (2), corresponde a la descripci´on de un
conjunto de esferas. Dos esferas se cortan en una circunferencia, una tercera
esfera corta a esta circunferencia en dos puntos, y una cuarta esfera resolver´ıa
la inc´ognita.
7

8. −10 −5 0 5 10 15 20 25
−5
0
5
10
15
20
Figura 3: Posicionamiento circular
3 Modelo de estimaci´on para posicionamiento v´ıa
sat´elite
3.1 Aplicaci´on del posicionamiento circular
Los sat´elites orbitando la tierra env´ıan se˜nales que los receptores captan
y procesan para determinar su posici´on. Existen dos procesos principales
de tratamiento de se˜nal. Por una parte se extraen datos codificados en la
se˜nal, y por otra se realizan una serie de medidas para poder determinar la
distancia del receptor al sat´elite. Los datos de navegaci´on extra´ıdos de la
se˜nal se utilizan para calcular las posiciones de los sat´elites xSi, as´ı como
para realizar correciones sobre las medidas de la se˜nal.
Existen tres tipos principales de medidas sobre la se˜nal: Pseudo-rangos de
C´odigo ρi, Pseudo-rangos de Fase Φi, y Efecto Doppler ˙ρi. Los pseudo-rangos
de c´odigo corresponden a las pseudo-distancias eucl´ıdeas que se utilizan en
el principio de posicionamiento circular. El prefijo pseudo procede de la
variaci´on entre distancias medidas y distancias reales. Los pseudo-rangos de
fase corresponden a la variaci´on en el n´umero de ciclos entre dos ´epocas
tk y tk+1. Se utilizan para refinar las medidas de c´odigo. Finalmente, las
observaciones Doppler sirven para determinar la velocidad relativa entre el
receptor y el sat´elite.
8

9. La se˜nal del sat´elite se codifica al menos de una manera (en el caso
del GPS son dos; c´odigo C/A, y c´odigo P). Esta codificaci´on se realiza
respecto a una base de tiempo determinada por un reloj at´omico de alta
precisi´on. Por otra parte el receptor genera este mismo c´odigo de manera
interna. Tras adquirir la se˜nal enviada por el sat´elite, en el receptor se realiza
una correlaci´on respecto a su se˜nal interna, a partir de la cual es posible
determinar el tiempo absoluto de propagaci´on de la se˜nal ∆˜ti. Este proceso
de correlaci´on se muestra en la gr´afica 4. El pseudo-rango de c´odigo en
metros se calcula multiplicando la velocidad c por el tiempo de propagaci´on
(3.1).
ρi = ∆˜ti · c (3)
Figura 4: Correlaci´on
Al no poderse medir de manera exacta el tiempo absoluto de propagaci´on
∆˜ti, los pseudo-rangos son tan s´olo una aproximaci´on de las distancias eu-
cl´ıdeas ρi = ri + . El error en el pseudo-rango depende del conocimiento
sobre las fuentes de error que afectan a la medida, y que podemos caracteri-
zar como
= c · (∆tr − δtSi) + Iρ + Tρ + 0, (4)
siendo ∆tr y δtSi los errores en los relojes del receptor y del sat´elite respecti-
vamente, Iρ y Tρlos retardos inducidos por capas de la atm´osfera (Ionosfera
y Troposfera), y donde 0 representa otras fuentes de error. Tanto el error en
el reloj del sat´elite como las variables que determinan el retardo ionosf´erico
se pueden calcular utilizando datos codificados sobre la se˜nal. El error tro-
posf´erico puede ser estimado bien empleando un modelo est´andar, o bien
utilizando sensores externos. El error en el reloj del receptor ∆tr pasar´a
a formar parte del vector de estado o conjunto de inc´ognitas a resolver
9

10. xzb = (xr, yr, zr, ∆tr). De esta manera obtenemos el siguiente sistema de
ecuaciones
ρ1 = xr − xS1 + c · ∆tr
· · ·
ρi = xr − xSi + c · ∆tr
· · ·
ρn = xr − xSn + c · δtr (5)
La existencia de errores en las distancias medidas hace que la soluci´on
geom´etrica del sistema no est´e formada por puntos de intersecci´on ideales
entre c’irculos o esferas, sino m´as bien regiones sobre las que hay que estimar
la posici´on del receptor, como es puede apreciar en la Figura 5.
Figura 5: Estimaci´on en sistemas de posicionamiento circulares
3.2 C´alculo de las posiciones de los sat´elites
Las posiciones de los puntos de referencia del sistema, en este caso los
sat´elites, se calculan a partir de unos datos llamados de efemeris que se ex-
traen de la se˜nal enviada de cada sat´elite. El proceso de c´alculo est´a definido
en los Documentos de Control de la Interfaz [13] y [14].
10

11. 3.2.1 Posiciones de los sat´elites de GPS
Los datos de efem´eris transmitidos por los sat´elites de GPS consisten por
una parte en los elementos que definen las ´orbitas Keplerianas [15], y por
otra en un conjunto de par´ametros para modelar las perturbaciones sufridas
por las posiciones de los sat´elites respecto a esas ´orbitas Keplerianas.
Las componentes de las ´orbitas Keplerianas son las siguientes. En primer
lugar el semieje mayor a y la excentricidad e, que definen la forma y el
tama˜no de la elipse que constituye la ´orbita. Adem´as est´an el argumento de
perigeo ω, la direcci´on del nodo ascendente Ω y la inclinaci´on i, que definen
el plano orbital sobre el que se encuentra la ´orbita. Por ´ultimo, la anomal´ıa
media µ, que define la posici´on del sat´elite sobre esta ´orbita.
En el proceso del c´alculo de las posiciones de los sat´elites de GPS se
pueden se˜nalar los siguientes pasos:
Paso 1. Correcci´on de la velocidad media del sat´elite
n =
µ
a3
+ δn. (6)
Paso 2. Tiempo transcurrido desde la creaci´on de los datos de efemeris
tk = t − t0e. (7)
Paso 3. Anomal´ıa media en el momento tk
Mk = M0 + n(tk). (8)
Paso 4. Anomal´ıa exc´entrica. Este paso se puede hacer empleando dis-
tintos m´etodos num´ericos, o incluso por simple iteraci´on. El m´etodo que se
mostr´o m´as efectivo tanto en el n´umero de operaciones como en la precisi´on
de la soluci´on fue el m´etodo de Newton-Raphson.
Ek = Ek − e · sin(Ek) (9)
Paso 5. Anomal´ıa verdadera vk. Se puede calcular vk de distintas man-
eras, a trav´es de equivalencias trigonom´etricas. A continuaci´on se muestran
dos de ellas.
sin(vk) =
√
1 − e2 · sin(ek)
1 − e · cos(Ek)
cos(vk) =
cos(Ek) − e
1 − e · cos(Ek)
(10)
Paso 6. Argumento de latitud
φk = vk + ω. (11)
11

12. Paso 7. Correci´on al argumento de latitud
δφk = Cus · sin(2φk) + Cuc · cos(2φk). (12)
Paso 8. Correci´on del radio
δrk = Crs · sin(2φk) + Crc · cos(2φk). (13)
Paso 9. Correci´on de la inclinaci´on
δik = Cis · sin(2φk) + Cic · cos(2φk). (14)
Paso 10. Argumento de latitud corregido
uk = φk + δφk. (15)
Paso 11. Radio corregido
rk = a · (1 − e · cos(Ek)) + δrk. (16)
Paso 12. Inclinaci´on corregida
ik = i0 +
∂i
∂t
tk + δik. (17)
Paso 13. Longitud del nodo corregida
Ωk = Ω0 + ( ˙Ω − ˙Ωe) · tk − ˙Ωe · t0e. (18)
Paso 14. Posici´on x en el plano orbital
xp = rk · cos(uk). (19)
Paso 15. Posici´on y en el plano orbital
yp = rk · sin(uk). (20)
Paso 16. Coordenada cartesiana Earth Centered Earth Fixed ECEF x
xs = xp · cos(Ωk) − yp · cos(ik) · sin(Ωk). (21)
Paso 17. Coordenada ECEF y
ys = xp · sin(Ωk) − yp · cos(ik) · cos(Ωk). (22)
Paso 18. Coordenada ECEF z
zs = yp · sin(ik). (23)
12

13. 3.2.2 Posiciones de los sat´elites GLONASS
El m´etodo de c´alculo de las posiciones de GLONASS difiere respecto al
m´etodo de GPS en que en GLONASS la posici´on actual se calcula a partir
de una posici´on anterior. Para ello se ha de aplicar una t´ecnica de integraci´on
num´erica al conjunto de ecuaciones diferenciales que describen el movimiento
de los sat´elites. Este conjunto de ecuaciones viene definido en el Documento
de Control de la Interfaz [14] de la siguiente manera.
∂x
∂t
= ˙x
∂y
∂t
= ˙y
∂z
∂t
= ˙z
∂ ˙x
∂t
= −
µ
r3
· x −
3
2
· J0
2
·
µ · a2
e
γ5
· x · 1 −
5 · z2
γ2
+ ω2
· x + 2ω · ˙y + ¨x
∂ ˙y
∂t
= −
µ
r3
· y −
3
2
· J0
2
·
µ · a2
e
γ5
· y · 1 −
5 · z2
γ2
+ ω2
· y + 2ω · ˙x + ¨y
∂ ˙z
∂t
= −
µ
r3
· z −
3
2
· J0
2
·
µ · a2
e
γ5
· z · 1 −
5 · z2
γ2
+ ¨z (24)
siendo r = x2 + y2 + z2, µ = 398600, 44 ∗ 109m3/s2 la constante grav-
itacional, ae = 6378136 m el semieje mayor de la tierra, J0
2
= 108262, 7·10−9
el segundo harm´onico zonal del geopotencial, ω = 7, 292115·10−5radianes/s
la velocidad de rotaci´on de la tierra, ˙x la velocidad del sat´elite en la direcci´on
del eje x, y ¨x su aceleraci´on.
Para llevar a cabo la integraci´on se puede aplicar el m´etodo de Runge
Kutta.
3.2.3 Conversi´on PZ-90 a WGS84
En GPS se utiliza el sistema de coordenadas WGS84, definido en [16], mien-
tras que GLONASS utiliza un sistema ruso denominado PZ-90. A pesar de
ser ambos sistemas de coordenadas cartesianos, y de tener el origen en el
centro de la tierra, existe una peque˜na diferencia entre ambos, que ha sido
objeto de estudio por diversos autores. Mitrikas en [17] propone para pasar
de un sistema a otro aplicar la siguiente matriz de conversi´on calculada a
partir de datos experimentales.
xT
W GS84=



−0,47
−0,51
−1,56


+(1+22·10−9)·



1 −1,728·10−6 −0,017·10−6
1,728·10−6 1 0,076·10−6
0,017·10−6 −0,076·10−6 1


·xT
P Z90
13

14. 3.3 Modelizaci´on de las fuentes de error
Como ya se ha introducido en el punto 3.1, existen diversas fuentes de error
que afectan a la exactitud de las medidas de distancia o pseudo-rango, y
por tanto tambi´en a la precisi´on final del sistema (la posici´on del receptor).
Las principales fuentes de error son las siguientes: los retardos atmosf´ericos
debidos a la ionosfera, a la troposfera y al denominado retardo de grupo, los
errores de sincronizaci´on de los relojes, tanto del sat´elite como del receptor,
los efectos relativ´ısticos sobre la transmisi´on se˜nal, y por ´ultimo los efectos
de multicamino debidos a la presencia de obst´aculos en el entorno inmediato
del receptor.
3.3.1 Retardo ionosf´erico
El retardo inducido en la se˜nal por la capa externa de la atm´osfera (entre 70
y 640 km) se debe principalmente a la presencia de electrones que influyen en
la propagaci´on normal de la se˜nal electromagn´etica. Este retardo var´ıa seg´un
la ´epoca del a˜no, la hora del d´ıa, y la posici´on geogr´afica del receptor. Existe
un modelo universalmente aceptado para su correcci´on que se denomina
Modelo de Klobuchar [18]. Este retardo en segundos se puede determinar a
trav´es de la expresi´on
Tg = DC + A · 1 −
x2
2
+
x4
24
para x ≤
π
2
(25)
donde x =
2·π·(t−Tp)
P (radianes), DC representa la constante de compensaci´on
y es igual a 5 ns, Tp representa la fase y es igual a 50400 s (14:00)y t represen-
ta la hora local. A y P representan la amplitud y el periodo respectivamente
y se calculan de la siguiente manera
A = 3
n=0 αnΦn
m P = 3
n=0 βnΦn
m.
donde αn, βn son coeficientes calculados por las estaciones de control de
GPS y posteriormente enviados a los receptores a trav´es de las se˜nales de los
sat´elites, y Φm es la latitud geomagn´etica del subpunto ionosf´erico. Para el
c´alculo de Φm es imprescindible realizar una serie de pasos cuya explicaci´on
desbordar´ıa los objetivos de este trabajo. La implementaci´on en matlab del
modelo de Klobuchar se encuentra entre las funciones adjuntas ”iono.m”.
3.3.2 Retardo troposf´erico
El retardo debido a la troposfera, situada entre la superficie de la tierra y
los primeros 18 km de la atm´osfera, ha sido objeto de estudio por parte de
muchos autores. Estos modelos utilizan principalmente medidas de presi´on
atmosf´erica, de humedad y temperatura para estimar el retardo de la se˜nal
del GPS. Tambi´en se han desarrollado modelos est´andar para receptores que
no cuentan con informaci´on atmosf´erica.
14

15. El retardo troposf´erico se puede definir como
To = (n − 1) ds (26)
donde n representa el ´ındice de refracci´on. Generalmente se utiliza la refrac-
tividad NT = 106 · (n − 1), en vez de n, para poder realizar la integraci´on a
lo largo del camino geom´etrico de la se˜nal, convirti´endose (26) en (27).
To = 10−6
NT
ds (27)
Entre los dos modelos m´as empleados para estimar To se encuentran el
propuesto por Saastamoinen, [20], y el propuesto por Hopfield, [19].
Hopfield propone separar NT en dos componentes: refractividad seca Nt
s
y refractividad h´umeda Nt
h, obteniendo:
To = 10−6
NT
s ds + 10−6
NT
h ds. (28)
Alrededor del 10 % del retardo troposf´erico proviene de la refractividad
seca y el 90 % de la h´umeda. Hopfield propone cuantificar estos retardos de
la siguiente manera
Tos =
10−6 · (77, 64 · p
T ) · [40136 + 148, 72 · (T − 273, 16)]
5 · sin( E2 + 6, 25)
(29)
Toh =
10−6 · e · 11000 · (−12, 96 + 3, 718 · 105)
5 · T2 · sin( E2 + 2, 25)
(30)
donde Tos y Toh representan respectivamente las componentes seca y h´umeda
del retardo troposf´erico, p la presi´on atmosf´erica en milibares, T la temper-
atura en grados Kelvin, e la presi´on parcial del vapor de agua en milibares,
y E la elevaci´on del sat´elite respecto del receptor.
Saastamoinen propone deducir la refractividad a partir de las leyes f´ısicas
sobre los gases. Para ello plantea el siguiente modelo.
To =
0, 002277
cos z
p +
1255
T
+ 0, 05 · e − tan2
z (31)
donde p, T, y e representan presi´on atmosf´erica, temperatura y presi´on del
vapor de agua, y z representa el ´angulo de apogeo (zenit) del sat´elite.
15

16. 3.4 Efectos relativ´ısticos
Debido a la diferencia entre la velocidad del sat´elite trazando su ´orbita
y el receptor desplaz´andose aproximadamente a la velocidad de rotaci´on
de la tierra , las distancias entre el sat´elite y el receptor en el momento
de env´ıo de la se˜nal, y en el momento de recepci´on de la misma no son
exactamente iguales. Esto se denomina efecto relativistico y la correcci´on
que ha de efectuarse sobre el pseudo-rango observado viene definida por
Trel =
2µ
c2
· ln
ρj + ρi + ρj
i
ρj + ρi − ρj
i
(32)
donde µ es la constante gravitacional de la tierra, ρj y ρi son las distancias
geoc´entricas del sat´elite y el receptor, y ρj
i la distancia entre el sat´elite y el
receptor.
3.5 Efecto multicamino
El efecto multicamino se debe a reflexiones de la se˜nal sobre obst´aculos
situados en un entorno inmediato del receptor. Al rebotar la se˜nal varias
veces sobre obst´aculos cercanos, la misma llega varias veces al receptor con
diferentes retardos. ´Esto hace que se pueda escoger por error una se˜nal
reflejada como se˜nal real, introduciendo un error en los pseudo-rangos.
No existe un modelo general para el efecto multicamino debido a las
diferentes condiciones geom´etricas en las que se puede encontrar el receptor.
Se han desarrollado sin embargo algunas soluciones para reducir y estimar
el efecto multicamino. ´Estas se pueden clasificar en tres grupos: mitigaci´on
basada en la antena, detecci´on basada en t´ecnicas de adquisici´on mejoradas
y tratamiento adicional de datos y se˜nal. Al no tener ninguno de estos grupos
una relaci´on directa con este trabajo, no se entrar´a en mayor detalle.
4 Soluci´on al sistema de ecuaciones que define la
navegaci´on v´ıa sat´elite
Una vez estimadas las posiciones de los sat´elites xSi y corregidas las me-
didas de pseudo-rango ρ, es posible tanto calcular la posici´on del receptor
(xr, yr, zr) como estimar el retardo de su reloj ∆tr. Sea xr = (xr, yr, zr, ∆tr)
el vector de estado del receptor, ρ = (ρ1, ρ2, . . . , ρn) el vector de pseudo-
distancias o pseudo-rangos medido, y xSi el conjunto de las posiciones de
los sat´elites visibles. Podemos definir el siguiente sistema de ecuaciones
ρ1 = xr − xS1 + c · ∆tr
16

17. · · ·
ρi = xr − xSi + c · ∆tr
· · ·
ρn = xr − xSn + c · ∆tr. (33)
4.1 M´etodo de Bancroft
S. Bancroft propone en [23] un m´etodo para resolver el sistema de ecuaciones
de GPS, que se puede utilizar tambi´en en sistemas que combinan medidas
de GPS+GLONASS, as´ı como para el futuro sistema GALILEO.
Se definen los vectores de datos ai = (xSi
T , ρi)T , con i = 1 . . . n, y la
matriz asociada A = (a1, . . . , ai, . . . , an)T .
A trav´es del funcional de Minkowski < t, q >= t1·q1+t2·q2+t3·q3−t4·q4,
se define m = (m1, . . . , mi, . . . , mn)T tal que mi =< ai, ai > /2.
La matriz de ponderaci´on W se define como la inversa de la matriz de
covarianza Σ de las medidas de pseudo-rango ρi. Utilizamos W para realizar
una proyecci´on obl´ıcua de A
B = (AT
· W · A)−1
· AT
· W. (34)
A partir de B calculamos u y v tales que
u = B · i0, i0 = (1, . . . , 1, . . . , 1)T
v = B · m.
Utilizando los vectores u y v podemos calcular los coeficientes E,F y G, que
definimos como
E = < u, u >
F = < u, v > −1
G = < v, v > .
Resolviendo la siguiente ecuaci´on de segundo grado,
E · λ2
+ 2 · F · λ + G = 0 (35)
obtenemos λ1 y λ2, que podemos utilizar para calcular dos posibles vectores
de estado del receptor
ˆxr = λ1,2 · u + v. (36)
Esta ambig¨uedad la resolvemos sustituyendo ˆxe1,2 en el sistema de ecua-
ciones original (33)
ρi = xr − xSi + c · ∆tr (37)
S´olo una de las dos soluciones se ajustar´a a las ecuaciones del sistema y ´esta
es la soluci´on buscada.
17

18. 4.2 Soluci´on mediante linealizaci´on por desarrollos de Taylor
Sea (xr, yr, zr) la posici´on real del receptor, y (ˆxr, ˆyr, ˆzr) una primera posi-
ci´on aproximada. Designamos (∆xr, ∆yr, ∆zr) como el vector distancia entre
las dos posiciones. Al desarrollar el sistema de ecuaciones (33) en una serie
de Taylor sobre la posici´on aproximada, podemos expresar el vector distan-
cia (∆xr, ∆yr, ∆zr) como funci´on lineal de las coordenadas conocidas y de
las medidas de pseudo-rango.
Sea un pseudo-rango ρi,
ρi = (xi − xr)2 + (yi − yr)2 + (zi − zr)2 + c · tr
= fi(xr, yr, zr, tr). (38)
Utilizando la posici´on aproximada (ˆxr, ˆyr, ˆzr) y la estimaci´on de error
en el tiempo ˆtr del reloj del receptor, se puede calcular un pseudo-rango
aproximado:
ˆρi = (xi − ˆxr)2 + (yi − ˆyr)2 + (zi − ˆzr)2 + c · ˆtr
= fi(ˆxr, ˆyr, ˆzr, ˆtr). (39)
La posici´on y el error de tiempo del receptor se pueden considerar for-
madas por una componente aproximada conocida y una componente incre-
mental desconocida.
xr = ˆxr + ∆xr
yr = ˆyr + ∆yr
zr = ˆxr + ∆xr
tr = ˆtr + ∆tr (40)
Se puede establecer, por tanto,
fi(xr, yr, zr, tr) = fi(ˆxr + ∆xr, ˆyr + ∆yr, ˆzr + ∆zr, ˆtr + ∆tr) (41)
Esta funci´on se puede desarrollar sobre el vector aproximado (ˆxr, ˆyr, ˆzr, ˆtr)
utilizando una serie de Taylor,
fi(ˆxr + ∆xr, ˆyr + ∆yr, ˆzr + ∆zr, ˆtr + ∆tr) = fi(ˆxr, ˆyr, ˆzr, ˆtr) +
∂fi(ˆxr, ˆyr, ˆzr, ˆtr)
∂ˆxr
· ∆xr+
18

19. +
δfi(ˆxr, ˆyr, ˆzr, ˆtr)
∂ˆyr
· ∆yr +
δfi(ˆxr, ˆyr, ˆzr, ˆtr)
∂ˆzr
· ∆zr +
∂fi(ˆxr, ˆyr, ˆzr, ˆtr)
∂ˆtr
· ∆tr (42)
Este desarrollo se reduce a las derivadas parciales de primer orden para
evitar t´erminos no lineales. Las derivadas parciales se eval´uan de la siguiente
manera,
∂fi(ˆxr, ˆyr, ˆzr, ˆtr)
∂ˆxr
= −
xi − ˆxu
ˆri
∂fi(ˆxr, ˆyr, ˆzr, ˆtr)
∂ˆyr
= −
yi − ˆyu
ˆri
∂fi(ˆxr, ˆyu, ˆzr, ˆtr)
∂ˆzr
= −
zi − ˆzu
ˆri
∂fi(ˆxr, ˆyr, ˆzr, ˆtr)
δˆtr
= c (43)
siendo ˆri = (xi − ˆxr)2 + (yi − ˆyr)2 + (zi − ˆzr)2
Al sustituir (39) en (42) y (43) se obtiene
ρi = ˆρi −
xi − ˆxr
ˆri
· ∆xr −
yi − ˆyr
ˆri
· ∆yr −
zi − ˆzr
ˆri
· ∆zr + c · ∆tr (44)
A continuaci´on se agrupan los t´erminos conocidos en el lado izquierdo
de la ecuaci´on, y las inc´ognitas en el lado derecho,
ˆρi − ρi =
xi − ˆxr
ˆri
· ∆xr +
yi − ˆyr
ˆri
· ∆yr +
zi − ˆzr
ˆri
· ∆zr − c · ∆tr (45)
4.3 Soluci´on iterativa
4.3.1 Filtrado de Kalman
Las soluciones anteriores al c´alculo de la posici´on de gps se pueden mejorar
si consideramos el receptor de gps como sistema din´amico, y estimamos su
posici´on de forma iterativa. Para ello, el filtro propuesto por R.E. Kalman
en [24] es el m´etodo m´as apropiado.
Sea Sz una serie temporal de m medidas, Sz={z1,...,zk−1,zk,zk+1,...,zm}, tales
que zk = {ρ1, ρ2, . . . , ρn}. Se puede estimar el vector (posici´on - velocidad)
xk+1 del sistema de manera m´as precisa, xk+1 = (xe, ye, ze, ˙xe, ˙ye, ˙ze) para
el instante tk+1, empleando las estimaciones de vector de estado anteriores:
x1, x2, . . . , xk. Esta estimaci´on se lleva a cabo en dos pasos denominados
”Actualizaci´on del estado por predicci´on”, y ”Actualizaci´on del estado por
nuevas observaciones”.
19

20. El filtro se inicializa empleando una soluci´on en forma cerrada para el
primer conjunto de pseudorangos. En el caso en el que se tenga informaci´on
adicional sobre la din´amica del receptor, por ejemplo a trav´es de sensores
de velocidad, se aplica a continuaci´on la actualizaci´on del estado por predic-
ci´on consistente en la estimaci´on a priori del vector de estado xk+1
(−) en
el pr´oximo instante de tiempo tk+1, utilizando la estimaci´on en el momen-
to actual tk del vector de estado xk
(+) y un modelo Φk que describa la
din´amica del sistema para el instante de tiempo tk. La matriz de Covarianza
Pk+1
(−)
del sistema se actualiza a partir de la covarianza actual Pk
(+)
, de
la covarianza del ruido din´amico Qk y del modelo din´amico Φk.
Estimaci´on a priori del vector de estado:
ˆx
(−)
k+1 = Φk ˆx
(+)
k (46)
Estimaci´on a priori de la covarianza:
Pk+1
(−)
= Φk Pk
(+)
Φk
T
+ Qk (47)
Si no se tiene conocimiento sobre la velocidad / aceleraci´on del sistema
a trav´es de sensores externos, se puede establecer el modelo din´amico Φk
del sistema utilizando un modelo de desplazamiento lineal, basado en las
ecuaciones fundamentales de la cinem´atica (77) y (78). A la actualizaci´on
del estado por predicci´on realizado a partir de (78) se le a˜nade el c´alculo
previo de la velocidad ˙xk del chip emisor en el instante tk (77).
˙xk =
xk − xk−1
tk − tk−1
(48)
y
xk+1 = xk + ˙xk · ∆t, (49)
siendo xk = (xe, ye, ze), ˙xk = ( ˙xe, ˙ye, ˙ze) y ∆t = tk+1 − tk.
Por tanto, la matriz Φk ser´a de la forma
Φk =









1 0 0 ∆t 0 0
0 1 0 0 ∆t 0
0 0 1 0 0 ∆t
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1









En el caso de la inicializaci´on sin conocimiento alguno de la din´amica
del sistema tomar´ıamos la soluci´on en forma cerrada como estimaci´on a
20

21. priori del vector de estado, y pasar´ıamos directamente al siguiente paso tras
obtener el siguiente conjunto de pseudorangos.
La actualizaci´on del estado por nuevas observaciones consiste en la esti-
maci´on a posteriori del vector de estado xk+1
(−) en el pr´oximo instante de
tiempo para el que se obtienen nuevas observaciones. Para poder llevar a
cabo esta actualizaci´on, es necesario calcular la matriz de ganancias Kk+1
correspondiente al instante de tiempo tk+1. Esta matriz pondera el peso del
nuevo conjunto de observaciones respecto a la estimaci´on existente o a pri-
ori. Para ello se realiza una comparaci´on de la matriz de covarianza P del
sistema con la matriz de covarianza Σ del nuevo conjunto de observaciones.
La matriz de ganancia se define como
Kk = Pk+1
(−)
Hk+1
T
· (Hk+1Pk+1
(−)
Hk+1
T
+ Σk+1)−1
, (50)
siendo H la matriz de ajuste a las observaciones. Esta matriz es necesaria
para poder establecer una correspondencia entre P y Σ, y se define como:
H =







∂ρ1
∂x
ρ1
∂y
ρ1
∂z
∂ρ2
∂x
∂ρ2
∂y
∂ρ2
∂z
...
...
...
∂ρn
∂x
∂ρn
∂y
∂ρn
∂z ,







siendo
∂ρi
∂x
= −
xRi − ˆxe
ˆri
∂ρi
∂y
= −
yRi − ˆye
ˆri
∂ρi
∂z
= −
zRi − ˆze
ˆri
.
En el caso en el que haya observaciones disponibles sobre el efecto doppler
de la se˜nal, o desplazamiento relativo del sat´elite i respecto al receptor ˙ρi,
se pueden incluir en la matriz de ajuste a las observaciones y as´ı estimar la
componente de velocidad del vector de estado.
A continuaci´on se actualiza tanto el vector de estado ˆx
(+)
k+1 como la
matriz de covarianza del sistema Pk+1
(+)
.
Estimaci´on a posteriori del vector de estado:
ˆx
(+)
k+1 = ˆx
(−)
k+1 + Kk+1 · zk+1 − hk+1 ˆx
(−)
k+1 . (51)
Estimaci´on a posteriori de la covarianza:
Pk+1
(+)
= Pk+1
(−)
− Kk+1Hk+1Pk+1
(−)
. (52)
21

22. 4.3.2 T´ecnicas de suavizado (o smoothing)
El filtro de Kalman en tiempo real trata de realizar una nueva estimaci´on
a partir de la informaci´on anterior. Sin embargo la estimaci´on en tiempo
real puede ser de menor importancia que la trayectoria para determinadas
aplicaciones de la navegaci´on v´ıa sat´elite. En este caso es posible mejorar
la estimaci´on del vector de estado xk para un instante tk, empleando la
estimaci´on xk+1 del instante siguiente tk+1.
Hofmann en [10] propone el siguiente m´etodo de suavizado para un filtro
de Kalman aplicado al GPS. Se define la matriz de ganancia G(tk+1,tk).
G(tk+1,tk) = PkΦ(tk+1,tk)P
(−1)
k Pk+1 (53)
El suavizado del filtro, o estimaci´on hacia atr´as ˘xk se realiza de la sigu-
iente manera.
˘xk = xk + G(tk+1,tk) · (˘xk+1 − xk+1) (54)
4.4 Medidas de precisi´on
Existen varias maneras de determinar la precisi´on de un receptor de nave-
gaci´on v´ıa sat´elite. Hofmann [10] recoge las m´as empleadas.
Sea x la suma de los cuadrados de n variables estoc´asticas independientes
con distribuci´on Gaussiana. Se define la funci´on de distribuci´on χ2 como
fn(x) =
1
2n/2Γ(n/2)
· x(n/2)−1
· e−x/2
(55)
siendo la funci´on Γ(n/2) para n > 0
Γ(n/2) =
inf
0
µ(n/2)−1
e−µ
dµ (56)
Para el caso unidimensional n = 1 y x = z2, la distribuci´on χ2 se con-
vierte en la distribuci´on Gaussiana de media 0 y varianza 1. Su probabilidad
asociada es por tanto
P1(−α < z < α) =
1
√
2π
α
−α
e−z2/2
dz (57)
La tabla siguiente muestra algunos valores num´ericos de P1, que corre-
sponden a las medidas de precisi´on unidimensionales.
22

23. α Probabilidad Notaci´on
0,67 0,5 Error Lineal Probable (ELP)
1 0,683 Nivel 1-Σ
2 0,954 Nivel 2-Σ
3 0,997 Nivel 3-Σ
Para el caso bidimensional n = 2 y x = z2
1 + z2
2, la funci´on de densidad
de la distribuci´on χ2 es f2(x) = 1
2e−x2. Su probabilidad asociada viene dada
por
P2(0 < x < α) = 1 − e−α/2
. (58)
A continuaci´on se muestran las medidas de precisi´on bidimensionales
m´as extendidas en posicionamiento v´ıa sate´elite.
√
α Probabilidad Notaci´on
1 0,394 1-Σ o elipse est´andar
1,18 0,5 Error Circular Probable (ECP)√
2 0,632 Distancia Cuadr´atica Media
2 0,865 Elipse 2-Sigma
3 0,989 Elipse 3-Sigma
Para el caso tridimensional n = 2 y x = z2
1 + z2
2 + z2
3, la probabilidad
asociada a la funci´on de densidad de la distribuci´on χ2 es
P3(0 < x < α) =
1
√
2π
α
0
√
x · e−x2/2
dx (59)
Las medidas de precisi´on en R3 m´as extendidas se encuentran en la
siguiente tabla.
√
α Probabilidad Notaci´on
1 0,199 1-Σ o elipsoide est´andar
1,53 0,5 Error Esf´erico Probable (EEP)√
3 0,61 Error Radial Esf´erico Medio
2 0,738 Elipsoide 2-Sigma
3 0,971 Elipsoide 3-Sigma
5 Programa de Matlab
En el diskette adjunto se incluye un programa de matlab para la estimaci´on
de la posici´on utilizando ficheros de datos de GPS. Los ficheros de datos
son del formato RINEX, definido en [25]. El programa utiliza tres tipos
de ficheros: de navegaci´on, de observaciones, y meteorol´ogico. Los datos se
extraen de los ficheros simulando el proceso de estimaci´on en tiempo real
que ocurre en un receptor de GPS.
23

24. Para poder utilizar el programa es necesario copiar el fichero comprimido
MatlabGPS al disco duro y extraer los archivos con un programa descompre-
sor. En el diskette se adjunta un programa descompresor basado en MS-DOS
llamado unzip.exe. Los archivos del diskette tambin pueden descargarse de
internet de las direcciones; http://www.geocities.com/javiblanch/MGPS.zip,
y http://www.geocities.com/javiblanch/unzip.zip. Al fichero unzip.zip descar-
gado de internet hay que cambiarle el nombre a unzip.exe.
Para ejecutar el programa es necesario llamar a la funci´on principal: es-
timacion gps.m, indicando los ficheros que se quieren procesar. Una llamada
t´ıpica ser´ıa;
>> estimacion gps(’madr2530.04o’, ’madr2530.04n’, ’madr2530.04m’);
La salida del programa consiste por una parte en el resultado num´erico
sobre la l´ınea de comandos de matlab, y por otra en una serie de gr´aficas y
un men´u.
La primera gr´afica 6 muestra la visibilidad de los sat´elites en las 12 horas
siguientes a la ´ultima estimaci´on realizada. Esta visibilidad se corresponde
con la capacidad de recibir las se˜nales de cada uno de los sat´elites desde la
´ultima posici´on calculada.
La segunda gr´afica 7 ilustra el error de la estimaci´on realizada a partir
de los datos extra´ıdos de los ficheros. El error se calcula como la distancia
eucl´ıdea entre el punto calculado y la posici´on de referencia recogida en la
cabecera del fichero de observaci´on. En la imagen se muestran las compo-
nentes vertical y horizontal del error de la posici´on. Como se puede apreciar,
el error vertical suele ser mayor que el horizontal.
La tercera gr´afica 8 muestra la progresi´on de la estimaci´on de cada una
de las componentes de la posici´on. En cada una de las gr´aficas individuales
se ilustra el valor ideal al que ha de tender el proceso de estimaci´on.
El Menu permite elegir entre ver la posici´on en una proyecci´on de Lam-
bert 9, en una proyecci´on Mercator, o en un modelo orbital desarrollado en
el marco de este proyecto de investigaci´on. Los mapas han sido obtenidos
del toolbox gratuito de mapas mmap [26].
24

25. Figura 6: Visibilidad de los sat´elites GPS
Figura 7: Error en la estimaci´on de la posici´on
25

26. Figura 8: Estimaci´on de las componentes de la posici´on
Figura 9: Estimaci´on de las componentes de la posici´on
26

27. 6 Introducci´on al posicionamiento hiperb´olico
El objetivo de los sistemas de posicionamiento hiperb´olicos es determinar
la posici´on desconocida de un chip emisor xe, a partir de un conjunto de
receptores de posici´on conocida {xR1, xR2, xR3, ..., xRn} y de se˜nales en radio
frecuencia producidas por el chip emisor.
En el caso m´as com´un, el emisor de la se˜nal es el punto de posici´on
desconocida a determinar por el sistema de posicionamiento hiperb´olico,
y los receptores son los puntos de referencia. Sin embargo, tambi´en ser´ıa
posible determinar la posici´on desconocida de un receptor a partir de varios
emisores, as´ı como de otros receptores de posiciones conocidas.
La diferencia principal entre los sistemas de posicionamiento hiperb´olicos
y los circulares es que en los hiperb´olicos los tiempos de propagaci´on de la
se˜nal entre emisor y receptor no se conocen de manera absoluta. Esto se debe
a que no se conoce el momento, que representaremos por ts (sending time),
en el que el emisor transmite la se˜nal. Los datos disponibles son ´unicamente
los tiempos de llegada de la se˜nal a los receptores.
Sea tai (time of arrival) el tiempo de llegada de la se˜nal al receptor i. La
diferencia de distancias entre el emisor y dos de los receptores
ri1 = xe − xRi − xe − xR1
se puede expresar a trav´es de las diferencias en los tiempos de llegada de la
se˜nal, que est´an representados por (tai − ta1). En efecto,
c · ((tai − ta1)) = c · ((tai − ta1) − ts + ts) = c · (∆ti − ∆t1) = ri − r1 = ri1
donde ts representa el tiempo de transmisi´on de la se˜nal, ∆ti el tiempo de
propagaci´on de la se˜nal transcurrido entre su transmisi´on y su recepci´on, ri
la distancia entre el chip emisor y el receptor i, y c representa la velocidad
de transmisi´on de la se˜nal.
Por otra parte, la diferencia de distancias ri1 se puede representar como
ri1 =
√
(xe−xri)2+(ye−yri)2+(ze−zri)2−
√
(xe−xr1)2+(ye−yr1)2+(ze−zr1)2
y a partir de ah´ı podemos construir el siguiente sistema de ecuaciones no
lineales
r21 = xe − xR2 − xe − xR1
r31 = xe − xR3 − xe − xR1
· · ·
27

28. ri1 = xe − xRi − xe − xR1
· · ·
rn1 = xe − xRn − xe − xR1 (60)
Cada ecuaci´on corresponde en R2 a la descripci´on de una hip´erbola, sobre
la cual se encuentra el receptor cuya posici´on queremos determinar. Una
segunda hip´erbola corta a la primera en dos puntos, y una tercera interseca
en uno s´olo con las otras dos. Son necesarias, por tanto, 3 hip´erbolas y 4
receptores de referencia para poder resolver el sistema de ecuaciones 1, como
puede observarse en la siguiente gr´afica
−100 −80 −60 −40 −20 0 20 40 60
−60
−40
−20
0
20
40
60
Hyperbolic Positioning
R4
R
3
R2
R
1
xs
r21
= |xs
−R2
|−|xs
−R1
|
r31
= |xs
−R3
|−|xs
−R1
|
r
41
= |xs
−R4
|−|xs
−R1
|
Figura 10: Estimaci´on hiperb´olica de la posici´on (r1, r2 son desconocidas)
7 Modelo de estimaci´on para posicionamiento hiperb´olico
7.1 Variables del modelo
En el c´alculo de la posici´on en sistemas hiperb´olicos participan las siguientes
variables:
1
En este punto alguien podr´ıa argumentar la no necesidad de un cuarto receptor, al
poderse construir una tercera hip´erbola a partir de la diferencia de distancias entre el
emisor y los receptores 2 y 3. Sin embargo, esta hip´erbola no aportar´ıa la informaci´on
suficiente, al generar una dependencia lineal respecto a las otras dos ; r32 = r3 − r2
→ r32 = r3 − r2 + r1 − r1 → r32 = (r3 − r1) − (r2 − r1) → r32 = r31 − r21, quod erat
demostrandum
28

29. En primer lugar la posici´on desconocida xe del emisor, o vector de estado
y un conjunto de n receptores de referencia i, cuyas posiciones se conocen
xR = {xR1, xR2, xR3, . . . , xRn}.
Aparece tambi´en un conjunto de n observaciones de tiempos de llega-
da de la se˜nal, que transformamos en un conjunto de n − 1 diferencias de
distancias entre el emisor y los n receptores
ta = {ta1, ta2, ta3, . . . , tan}
r1 = {r21, r31, . . . , rn1.}
7.2 Fuentes de error
Existen una serie de fuentes de error que influyen sobre las medidas que se
toman de tiempos de llegada de la se˜nal. Una primera dificultad es la pres-
encia de obst´aculos a lo largo de la propagaci´on de la se˜nal, que puede pro-
ducir apantallamientos y reflexiones. Tambi´en pueden producir distorsiones
otras se˜nales que hayan sido emitidas en frecuencias parecidas. Asimismo
la presencia de obst´aculos alrededor del receptor puede producir el efecto
multicamino, o la apariencia de llegadas m´ultiples de la se˜nal, al rebotar
´esta sobre los obst´aculos. Sin embargo la mayor fuente de incertidumbre son
las propias limitaciones de precisi´on del sistema a la hora de establecer el
tiempo de llegada de la se˜nal.
El proceso de recepci´on de la se˜nal incluye la correlaci´on de la se˜nal
propagada con una generada internamente, as´ı como la asignaci´on de un
tiempo de llegada a esta se˜nal. Este proceso se ve influ´ıdo por la discretizaci´on
tanto de los componentes electr´onicos que realizan la correlaci´on (o identifi-
caci´on), como por la exactitud de la base de tiempo del receptor. Este error
se puede representar por tanto como una componente de error com´un, en
forma de ruido Gaussiano, que comparten todos los pseudorangos.
tai = tai+ i → c·((tai−ta1)) = c·((tai−ta1+ i+ 1)) → ri1 = ri−r1+c·( i+ 1)
Definiendo σr(2) = σr21 , y σr(2)r(3) = σr21r31 , se puede establecer la siguiente
matriz de covarianzas Σ de las observaciones transformadas ri1.
Σ =






σ2
r(2) σr(2)r(3) . . . σr(2)r(n)
σr(3)r(2) σ2
r(3) . . . σr(3)r(n)
...
...
...
...
σr(n)r(2) σr(n)r(3) . . . σ2
r(n)






El problema real del posicionamiento hiperb´olico se puede ver utilizando la
siguiente gr´afica, en la que se puede observar que las hip´erbolas no se cortan
en dos puntos, sino m´as bien en regiones.
29

30. −100 −80 −60 −40 −20 0 20 40 60
−60
−40
−20
0
20
40
60
R
4
R1
R
2
R3
Measurement error and hyperbolic positioning
x
s
’r
21
’r
31
’r
41
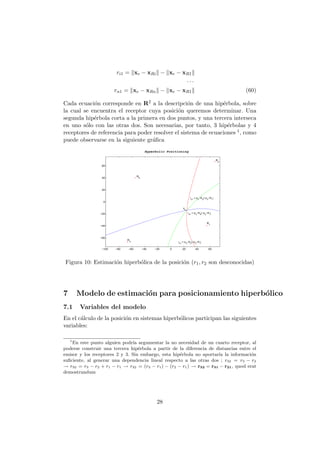
Figura 11: Problema real del posicionamiento hiperb´olico
8 Disposici´on geom´etrica de los receptores
La disposici´on geom´etrica de los receptores juega un papel fundamental en
la precisi´on final del sistema. K.C. Ho e Y.T. Chan proponen un an´alisis
de la disposici´on geom´etrica en [21] para la aplicaci´on del principio de posi-
cionamiento hip´erbolico a la navegaci´on v´ıa sat´elite. Para los sistemas de
posicionamiento locales, esta disposici´on ha de establecerse en base a dos
criterios: buscar la mayor distancia posible entre el emisor y los receptores,
y conseguir la mayor ortogonalidad posible en las intersecciones entre las
hip´erbolas.
Como ha sido introducido en el punto anterior, la fuente principal de
error del sistema es la propia limitaci´on en la base de tiempo de los recep-
tores. Esto produce un error constante sobre las medidas, cuya influencia en
la precisi´on sistema se reduce al aumentar la distancia entre el emisor y el
receptor. Para un sistema de posicionamiento local es importante por tanto
lograr la mayor distancia en las tres direcciones entre receptor y emisor.
Debido a los diferentes errores que afectan a las observaciones del sis-
tema, la intersecci´on entre dos hip´erbolas se representa por dos regiones en
vez de por dos puntos. Estas dos regiones tendr´an un tama˜no menor cuanto
m´as ortogonal sea la intersecci´on. La manera de conseguir la mayor ortogo-
nalidad en las intersecciones es disponiendo los receptores en R2 formando
un pol´ıgono regular, y en R3 formando un poliedro regular. As´ı, en el caso
de un sistema de cuatro receptores su configuraci´on ideal ser´ıa un tetraedro
30

31. que encerrase en su centro de masas la zona por la que se desplacen los
emisores.
Las restricciones f´ısicas de los entornos, en los que se pueden instalar
sistemas de posicionamiento locales, impiden que los receptores puedan ser
colocados a una distancia infinita de los emisores, o formando poliedros
perfectamente regulares. Por este motivo, al decidir la disposici´on geom´etrica
de los receptores, hay que tratar de cumplir estos dos criterios en la medida
de lo posible. Las siguientes gr´aficas muestran un an´alisis de c´omo se diluye
la precisi´on del sistema seg´un se elija una configuraci´on u otra.
−80 −60 −40 −20 0 20 40 60 80
−50
−40
−30
−20
−10
0
10
20
30
40
50
8 Receptores − Geometria favorable
Error Medio XYZ = 46.11 cm
Error Medio XY = 9.01 cm
Error Maximo XYZ = 81.46 cm
Error Maximo XY = 29.75 cm
Error Minimo XYZ = 25.77 cm
Error Minimo XY = 3.71 cm
Figura 12: Disoluci´on de la precisi´on en una geometr´ıa desfavorable
31

32. −80 −60 −40 −20 0 20 40 60 80
−50
−40
−30
−20
−10
0
10
20
30
40
50
8 Receptores − Geometria desfavorable
Error Minimo XYZ = 47.32 cm
Error Minimo XY = 5.48 cm Error Maximo XYZ = 162.91 cm
Error Maximo XY = 50.24 cm
Error Medio XYZ= 83.25 cm
Error Medio XY= 17.39 cm
Figura 13: Disoluci´on de la precisi´on en una geometr´ıa favorable
9 Soluci´on al sistema de ecuaciones que define el
posicionamiento hiperb´olico
9.1 Introducci´on
Como ya hemos dicho en la introducci´on, la resoluci´on del sistema de ecua-
ciones (60) define el problema del posicionamiento hiperb´olico,
r21 = xe − xR2 − xe − xR1
r31 = xe − xR3 − xe − xR1
· · ·
ri1 = xe − xRi − xe − xR1
· · ·
rn1 = xe − xRn − xe − xR1 . (60)
Existen diversas t´ecnicas para la resoluci´on de este conjunto de ecuaciones no
lineales. B. T. Fang [22] propone una soluci´on en forma cerrada directamente
dise˜nada para la resoluci´on de (60). Adem´as, debido a la similitud de (60) con
el sistema de ecuaciones del posicionamiento v´ıa sat´elite, se pueden aplicar
pr´acticamente los mismos m´etodos sin m´as que adapt´arlos a (60). Este es
el caso del m´etodo propuesto por S. Bancroft [23] para la resoluci´on de las
ecuaciones de GPS, y cuya adaptaci´on al problema hiperb´olico se explica en
32

33. la siguiente secci´on. Asimismo se puede linealizar (60) utilizando desarrollos
de Taylor.
En el caso de que durante un intervalo de tiempo se pueda contar con
varias observaciones distribuidas a lo largo del intervalo, se pueden utilizar
t´ecnicas de filtrado de Kalman, que permiten alcanzar una mayor precisi´on
en la estimaci´on de la posici´on.
9.2 El m´etodo de Bancroft aplicado al sistema hiperb´olico
Sean xe las coordenadas del chip emisor a localizar, y xRi las coordenadas
conocidas de los receptores. Partiendo de los tiempos de llegada de la se˜nal
a los receptores ˜tai = tai + , podemos construir la diferencia de tiempos de
llegada respecto a la primera recepci´on, ˜tai1 = tai − ta1 + . Multiplicando
por la velocidad de propagaci´on de la se˜nal, c, obtenemos una estimaci´on
de ˜ri1, que es la diferencia entre la distancia ri del emisor al receptor i y la
distancia r1 del emisor al receptor 1. Se tiene entonces
c · ˜tai1 = c · (tai − ta1) + = c · (tai − ts) − (ta1 − ts) + = ri − r1 + .
Por tanto
c · ˜tai1 = ˜ri1.
Definimos los vectores de datos ai = (xRi
T , ˜ri1)T , con i = 2 . . . n, y
formamos la matriz A = (a2, . . . , ai, . . . , an)T .
A trav´es del funcional de Minkowski < t, q >= t1·q1+t2·q2+t3·q3−t4·q4,
definimos m = (m2, . . . , mi, . . . , mn)T tal que mi =< ai, ai > /2.
La matriz de ponderaci´on W se define c´omo la inversa de la matriz de
covarianza Σ de las medidas de distancias ri1. Utilizamos W para realizar
una proyecci´on oblicua de A
B = (AT
· W · A)−1
· AT
· W. (61)
A partir de B calculamos u y v tales que
u = B · i0, i0 = (1, . . . , 1, . . . , 1)T
v = B · m.
Utilizando los vectores u y v podemos calcular los coeficientes E,F y G, que
definimos como
E = < u, u >
F = < u, v > −1
G = < v, v > .
33

34. Resolviendo la siguiente ecuaci´on de segundo grado,
E · λ2
+ 2 · F · λ + G = 0 (62)
obtenemos λ1 y λ2, que podemos utilizar para calcular dos posibles posi-
ciones del emisor
ˆxe1,2 = λ1,2 · u + v. (63)
Esta ambig¨uedad la resolvemos sustituyendo ˆxe1,2 en las ecuaciones origi-
nales de las diferencias de distancias ri1
ri1 = ||xRi − ˆxe1,2|| − ||xR1 − ˆxe1,2||. (64)
S´olo una de las dos soluciones se ajustar´a a las ecuaciones.
9.3 Soluci´on mediante linealizaci´on por desarrollos de Taylor
Sea (xe, ye, ze) la posici´on real del emisor, y sea (ˆxe, ˆye, ˆze) una primera posi-
ci´on aproximada; designamos (∆xe, ∆ye, ∆ze) como el vector distancia entre
las dos posiciones. Al expandir el sistema de ecuaciones (60) en un desar-
rollo de Taylor sobre la posici´on aproximada, podemos expresar el vector
distancia (∆xe, ∆ye, ∆ze) como funci´on lineal de las coordenadas conocidas
y de las medidas de diferencias de distancias ri1.
Sea ˜ri1 la medida de diferencias de distancias definida como
˜ri1 =
√
(xRi−xe)2+(yRi−ye)2+(zRi−ze)2−
√
(xR1−xe)2+(yR1−ye)2+(zR1−ze)2+
= xRi − xe − xR1 − xe +
= fi(xe, ye, ze) + ε (65)
tal que xRi = (xRi, yRi, zRi), i = 1, . . . , n, xe = (xe, ye, ze).
Utilizando la posici´on aproximada (ˆxe, ˆye, ˆze) y las posiciones conocidas
de los receptores xRi se puede calcular una diferencia de distancias aproxi-
mada:
ˆri1 = xRi − ˆxe − xR1 − ˆxe
= fi(ˆxe, ˆye, ˆze). (66)
La posici´on del emisor se puede considerar formada por una componente
aproximada conocida y una componente incremental desconocida:
xe = ˆxe + ∆xe
ye = ˆye + ∆ye
ze = ˆxe + ∆xe. (67)
34

35. Se puede establecer, por tanto,
fi(xe, ye, ze) = fi(ˆxe + ∆xe, ˆye + ∆ye, ˆze + ∆ze). (68)
Esta funci´on se puede expresar en funci´on del vector (ˆxe, ˆye, ˆze) utilizando
un desarrollo de Taylor de primer orden
fi(ˆxe+∆xe,ˆye+∆ye,ˆze+∆ze)≈fi(ˆxe,ˆye,ˆze)+
∂fi(ˆxe,ˆye,ˆze)
∂ˆxe
·∆xe+
+
∂fi(ˆxe,ˆye,ˆze)
∂ ˆye
·∆ye+
∂fi(ˆxe,ˆye,ˆze)
∂ˆze
·∆ze. (69)
La aproximaci´on se reduce a las derivadas parciales de primer orden para
evitar t´erminos no lineales. Las derivadas parciales se eval´uan de la siguiente
manera,
∂fi(ˆxe, ˆye, ˆze)
∂ˆxe
= −
xRi − ˆxe
ˆri
+
xR1 − ˆxe
ˆr1
∂fi(ˆxe, ˆye, ˆze)
∂ˆye
= −
yRi − ˆye
ˆri
+
yR1 − ˆye
ˆr1
∂fi(ˆxe, ˆye, ˆze)
∂ˆze
= −
zRi − ˆze
ˆri
+
zR1 − ˆze
ˆr1
, (70)
siendo ˆri = (xRi − ˆxe)2 + (yRi − ˆye)2 + (zRi − ˆze)2.
Con el prop´osito de simplificar se introducen nuevas variables
∆ρi = ˆri1 − ˜ri1 − ε
axi =
∂fi(ˆxe, ˆye, ˆze)
∂ˆxe
ayi =
∂fi(ˆxe, ˆye, ˆze)
∂ˆye
azi =
∂fi(ˆxe, ˆye, ˆze)
∂ˆze
(71)
De esta manera, la ecuaci´on (69) puede escribirse c´omo
∆ρi = axi · ∆xe + ayi · ∆ye + azi · ∆ze, con 1 ≤ i ≤ n. (72)
Para resolver el sistema de ecuaciones representado en (72) se definen
las siguientes matrices
35

36. ∆ρ =






∆ρ2
∆ρ3
...
∆ρn






H =






ax2 ay2 az2
ax3 ay3 az3
...
...
...
axn ayn azn






∆x =



∆xe
∆ye
∆ze


 .
Con esta notaci´on, la expresi´on (72) se puede representar como
∆ρ = H · ∆x, (73)
que tiene como soluci´on
∆x = (HT
· H)
−1
· HT
· ∆ρ. (74)
Una vez que se han despejado las inc´ognitas es posible calcular la posi-
ci´on del chip emisor (ˆxe, ˆye, ˆze). Utilizando esta nueva posici´on, se puede
estimar un nuevo vector de diferencias de distancias ˆri1, e iterar el pro-
cedimiento hasta alcanzar un criterio de convergencia Crit. Este criterio se
puede establecer como la distancia m´axima permitida entre estimaciones de
dos iteraciones consecutivas:
Convergencia → xk − xk−1 < Crit.
9.4 El filtro de Kalman y el posicionamiento hiperb´olico
Las t´ecnicas de filtrado propuestas por R.E. Kalman en [24] se pueden uti-
lizar tambi´en para resolver el problema del posicionamiento hiperb´olico, de
una manera similar a la empleada para resolver el problema de la navegaci´on
v´ıa sat´elite.
Sea Sz una serie temporal de m medidas, Sz={z1,...,zk−1,zk,zk+1,...,zm}, tales
que zk = {r21, r31, . . . , rn1}. Se puede realizar una estimaci´on m´as precisa del
estado (posici´on - velocidad) xk+1 del sistema, xk+1 = (xe, ye, ze, ˙xe, ˙ye, ˙ze)
para el instante tk+1, a trav´es de las estimaciones de vector de estado ante-
riores: x1, x2, . . . , xk. Esta estimaci´on se realiza en dos pasos denominados
”Actualizaci´on del estado por predicci´on”, y ”Actualizaci´on del estado por
nuevas observaciones”.
La actualizaci´on del estado por predicci´on consiste en la estimaci´on a
priori del vector de estado xk+1
(−) en el pr´oximo instante de tiempo tk+1,
utilizando la estimaci´on en el momento actual tk del vector de estado xk
(+),
y un modelo Φk que describa la din´amica del sistema para el instante de
tiempo tk. La matriz de Covarianza Pk+1
(−)
del sistema se actualiza a partir
de la covarianza actual Pk
(+)
, de la covarianza del ruido din´amico Qk y del
modelo din´amico Φk.
36

37. Estimaci´on a priori del vector de estado:
ˆx
(−)
k+1 = Φk ˆx
(+)
k (75)
Estimaci´on a priori de la covarianza:
Pk+1
(−)
= Φk Pk
(+)
Φk
T
+ Qk (76)
En el caso del posicionamiento hiperb´olico, el modelo din´amico Φk del
sistema se establece utilizando un modelo de desplazamiento lineal, basado
en las ecuaciones fundamentales de la cinem´atica (77) y (78). A la actual-
izaci´on del estado por predicci´on realizado a partir de (78) se le a˜nade el
c´alculo previo de la velocidad ˙xk del chip emisor en el instante tk (77).
˙xk =
xk − xk−1
tk − tk−1
(77)
y
xk+1 = xk + ˙xk · ∆t, (78)
siendo xk = (xe, ye, ze), ˙xk = ( ˙xe, ˙ye, ˙ze) y ∆t = tk+1 − tk.
Por tanto, la matriz Φk ser´a de la forma
Φk =









1 0 0 ∆t 0 0
0 1 0 0 ∆t 0
0 0 1 0 0 ∆t
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1









Este modelo podr´ıa extenderse ampliando el vector de estado con la
estimaci´on de la aceleraci´on del sistema, aunque esto s´olo es recomendable
para el caso de sistemas altamente din´amicos.
La actualizaci´on del estado por nuevas observaciones consiste en la esti-
maci´on a posteriori del vector de estado xk+1
(−) en el pr´oximo instante de
tiempo para el que se obtienen nuevas observaciones. Para poder llevar a
cabo esta actualizaci´on, es necesario calcular la matriz de ganancias Kk+1
correspondiente al instante de tiempo tk+1. Esta matriz pondera el peso del
nuevo conjunto de observaciones respecto a la estimaci´on existente o a pri-
ori. Para ello se realiza una comparaci´on de la matriz de covarianza P del
sistema con la matriz de covarianza Σ del nuevo conjunto de observaciones.
La matriz de ganancia se define como
Kk = Pk+1
(−)
Hk+1
T
· (Hk+1Pk+1
(−)
Hk+1
T
+ Σk+1)−1
, (79)
37

38. siendo H la matriz de ajuste a las observaciones. Esta matriz es necesaria
para poder establecer una correspondencia entre P y Σ, y se define como:
H =







∂r21
∂x
∂r21
∂y
∂r21
∂z
∂r31
∂x
∂r31
∂y
∂r31
∂z
...
...
...
∂rn1
∂x
∂rn1
∂y
∂rn1
∂z ,







siendo
∂ri1
∂x
= −
xRi − ˆxe
ˆri
+
xR1 − ˆxe
ˆr1
∂ri1
∂y
= −
yRi − ˆye
ˆri
+
yR1 − ˆye
ˆr1
∂ri1
∂z
= −
zRi − ˆze
ˆri
+
zR1 − ˆze
ˆr1
.
Es importante destacar que, al no disponer de medidas sobre la velocidad
del sistema, este paso del filtro de Kalman s´olo se aplica a las componentes
de posici´on del sistema (x). El siguiente paso es actualizar las estimaciones
de las componentes de posici´on tanto del vector de estado del sistema ˆx
(+)
k+1
como de la matriz de covarianza del sistema Pk+1
(+)
.
Estimaci´on a posteriori del vector de estado:
ˆx
(+)
k+1 = ˆx
(−)
k+1 + Kk+1 · zk+1 − hk+1 ˆx
(−)
k+1 . (80)
Estimaci´on a posteriori de la covarianza:
Pk+1
(+)
= Pk+1
(−)
− Kk+1Hk+1Pk+1
(−)
. (81)
10 Inicializaci´on del sistema
10.1 Introducci´on
Existen fuentes de error que afectan al sistema y se pueden minimizar en una
fase previa o de inicializaci´on. Para ello se pueden utilizar varios emisores de
referencia as´ı como un modelo de estimaci´on adecuado. Las dos principales
fuentes de error cuya influencia debemos reducir empleando un filtro inicial
son, por una parte la posici´on real de los puntos de referencia y por otra la
sincronizaci´on de los relojes de los receptores.
Para resolver el problema de la inicializaci´on del sistema, se introducen
nuevos puntos de referencia, es decir, chips emisores que se colocan sobre
posiciones fijas conocidas, xek, k = 1, . . . , m .
38

39. 10.2 Posici´on real de los puntos de referencia
Tanto los emisores como los receptores de referencia se colocan en sus posi-
ciones empleando unos medidores de distancia basados en tecnolog´ıa l´aser
que permiten determinar su posici´on real con una resoluci´on de cent´ımetros.
Sin embargo, el hecho de que el proceso de colocaci´on y medida respecto
al origen de coordenadas se realice manualmente a˜nade un error adicional al
sistema. ´Esto, unido al desconocimiento del centro de fase real de la antena
(diferente al centro f´ısico), as´ı como a otros efectos f´ısicos, introduce una
incertidumbre sobre la posici´on de los puntos de referencia.
10.3 Ajuste de la posici´on real de los puntos de referencia
Sea xref = (xe1, . . . , xem, xrec1, . . . , xrecn) el vector de posiciones reales de
los puntos de referencia, donde xek representa cada una de las posiciones de
los emisores de referencia, y xreci las posiciones de las antenas de los recep-
tores de referencia. Partiendo de las posiciones aproximadas de los puntos
de referencia xref = xref + , y utilizando medidas de diferencia de rango
rijk, el objetivo es minimizar los errores , en las posiciones de los puntos de
referencia. Recordemos,
ri1k = xreci − xek − xrec1 − xek
donde xreci − xek = (xek − xreci)2 + (yek − yreci)2 + (zek − zreci)2
Para resolver este problema podemos aplicar un m´etodo de m´ınimos
cuadrados iterativo, ponderando cada iteraci´on con la matriz de covarianza
de las medidas Σ. Sin embargo, contamos con la restricci´on a˜nadida que
supone no tener una estimaci´on fiable del error en las posiciones iniciales .
Como primer paso calculamos la matriz Jacobiana H del sistema de
ecuaciones rijk, o matriz de sensibilidad a las observaciones, respecto del
vector de las posiciones de referencia xref
H =
∂ri1k
∂xref
, (82)
39

40. H =


















∂r211
∂xe1
· · · 0 · · · 0 ∂r211
∂xrec1
∂r211
∂xrec2
0 · · · 0
∂r311
∂xe1
· · · 0 · · · 0 ∂r311
∂xrec1
0 ∂r311
∂xrec3
· · · 0
...
...
...
...
...
...
...
...
...
...
∂rn11
∂xe1
· · · 0 · · · 0 ∂rn11
∂xrec1
0 0 · · · ∂rn11
∂xrecn
...
...
...
...
...
...
...
...
...
...
0 · · · ∂ri1k
∂xek
· · · 0 ∂ri1k
∂xrec1
0 0 ∂ri1k
∂xreci
0
...
...
...
...
...
...
...
...
...
...
0 · · · 0 · · · ∂rn1m
∂xem
∂rn1m
∂xrec1
0 0 · · · ∂rn1m
∂xrecn


















donde cada uno de los cocientes ∂ri1k
∂xek
y ∂ri1k
∂xreci
representa a los vectores
∂ri1k
∂xek
= ∂ri1k
∂xek
∂ri1k
∂yek
∂ri1k
∂zek
∂ri1k
∂xreci
= ∂ri1k
∂xreci
∂ri1k
∂yreci
∂ri1k
∂zreci
,
siendo
δri1k
δyek
=
yek − yreci
|xreci − xek
−
yek − yrec1
xrec1 − xek
δri1k
δyrec1
=
yrec1 − yek
xrec1 − xek
δri1k
δyreci
=
yreci − yek
xreci − xek
El segundo paso ser´a calcular la matriz de ganancia para poder ponder-
ar el peso de cada conjunto nuevo de observaciones respecto del valor ya
estimado
K =
P · HT
H · P · HT + Σ
, (83)
donde Σ representa la matriz de covarianza de las medidas conocidas, y P la
matriz de covarianza del proceso (o del vector de estado xref . En la primera
iteraci´on tendremos el problema de no contar con una estimaci´on fiable del
error en las posiciones iniciales . Por ello, seleccionaremos una matriz de
covarianza inicial P exageradamente grande, que se ir´a ajustando a su valor
real seg´un vaya aumentando el n´umero de iteraciones.
El tercer paso consiste en calcular el vector de observaciones esperado,
aplicando la funci´on no lineal h(xref ) al vector de estado estimado hasta el
momento. Esta funci´on no es otra que el propio sistema de ecuaciones rijk.
Aplicamos por tanto
h(xref ) = xreci − xek − xrec1 − xek . (84)
40

41. A continuaci´on utilizamos el vector de observaciones esperado h(xref ), el
vector de observaciones obtenido z y la matriz de ganancia K para estimar el
nuevo vector de estado xref . Igualmente utilizaremos la matriz de ganancia
K y la matriz de sensibilidad a las observaciones H para actualizar la matriz
de covarianza del proceso P.
xref
(+)
= xref
(−)
+ K z − h(xref
(−)
) (85)
P(+)
= P(−)
− K · H · P (86)
Finalmente realizaremos un test de convergencia, y en caso de no cumplir-
lo volveremos al primer paso utilizando el nuevo vector de estado. Como
criterio de convergencia Critconv podemos utilizar la distancia entre los vec-
tores de estado a a priori y a posteriori.
Critconv → xref
(+)
− xref
(−)
≤ (87)
10.4 Sincronizaci´on de los relojes de los receptores
Debido a la distancia entre los receptores y el ordenador central en el que se
procesan los datos de las observaciones, al inicializar el sistema se produce
un error de sincronizaci´on en los relojes de los receptores. Una desviaci´on
de 10ns en el reloj de un receptor puede suponer un error de hasta 10 · c ≈
30cm en las observaciones. Por este motivo es necesario reducir este error
de sincronizaci´on inicial mediante un m´etodo de estimaci´on adecuado.
Sea b el vector que representa los errores de sincronizaci´on de los recep-
tores b = {b1, b2, . . . , bi, . . . , bn}, z el vector de observaciones de diferencia
entre el vector o de los tiempos de llegada, o = {o211, · · · , oi1k, . . . , on1m}
para n receptores y m emisores de referencia, y el vector de diferencia de
tiempos de llegada esperado h, h = {h211, · · · , hi1k, . . . , hn1m}, calculado
a partir de las posiciones de los puntos de referencia xref . Para cada k,
k = 1, . . . , m podemos establecer el siguiente sistema de ecuaciones
bi − b1 = oi1k − hi1k, (88)
donde
hi1k =
xreci − xek − xrec1 − xek
c
, c = velocidad de propagaci´on. (89)
Tenemos por tanto para cada valor de k un sistema de n−1 ecuaciones y
n inc´ognitas que podemos aproximar mediante un m´etodo iterativo similar
al del problema anterior. Tomaremos como vector de estado bx el vector
de desviaciones de los relojes, bx = {bx1 , bx2 , . . . , bxi , . . . , bxn }. Asimismo, el
41

42. vector de medidas que consideraremos ser´a el vector de desviaciones obser-
vadas z = {(o211 −h211), . . . , (oi1k −hi1k), . . . , (on1m −hn1m)}. Como primer
paso, calculamos la matriz Jacobiana H del sistema de ecuaciones bi1, (o ma-
triz de sensibilidad a las observaciones) sobre el vector de las desviaciones
de los relojes
H =
∂bi1
∂bx
(90)
H =





























−1 1 0 · · · 0 · · · 0 · · · 0 · · · 0
−1 0 1 0 0 · · · 0 · · · 0 · · · 0
...
...
...
...
...
...
...
...
...
...
...
−1 0 0 · · · 0 · · · 0 · · · 0 · · · 1
−1 1 0 · · · 0 · · · 0 · · · 0 · · · 0
−1 0 1 0 0 · · · 0 · · · 0 · · · 0
...
...
...
...
...
...
...
...
...
...
...
−1 0 0 · · · · · · 0 · · · 0 · · · 0 1
...
...
...
...
...
...
...
...
...
...
...
−1 1 0 0 0 · · · 0 · · · 0 · · · 0
−1 0 1 0 · · · 0 · · · 0 · · · 0 0
...
...
...
...
...
...
...
...
...
...
...
−1 0 0 0 · · · 0 · · · 0 · · · 0 1





























al ser δbi1
δbx(i) = 1.
El segundo paso ser´a calcular la matriz de ganancia K
K =
P · HT
H · P · HT + Σ
, (91)
donde Σ representa la matriz de covarianza de las medidas conocidas, y P la
matriz de covarianza del proceso (o del vector de estado bx) . En la primera
iteraci´on seremos conservadores, y tomaremos la diagonal de P (o varianza
de los errores) como el cuadrado del error m´aximo esperado, σbx = 100ns;
como covarianzas tomaremos una d´ecima parte de este error, σbxibxj = 10ns.
En el tercer paso calcularemos el vector de observaciones esperado. En la
primera iteraci´on tomaremos bx = {10, · · · , 10}, por ser 10ns la desviaci´on
m´axima esperada. Al ser un sistema lineal, se reduce a multiplicar la matriz
de sensibilidad a las medidas por el vector de estado actual
h(bx) = H · bx. (92)
42

43. Como cuarto paso estimamos el nuevo vector de estado bx
(+)
y la nueva
matriz de covarianza del proceso P.
bx
(+)
= bx
(−)
+ K z − h(bx
(−)
) (93)
P(+)
= P(−)
− K · H · P(−)
(94)
Finalmente aplicaremos el test de convergencia y en caso de no cumplirlo
volveremos al paso 1.
Critconv → bx
(+)
− bx
(−)
≤ (95)
10.5 Resoluci´on de la inicializaci´on por partes
Como es l´ogico, los errores de inicializaci´on influyen el uno sobre el otro y
no se pueden resolver de forma separada, por lo que es necesario resolverlos
a la vez. La siguiente figura muestra como combinar los dos m´etodos en un
solo filtro. El flujo del filtro depender´a de la calidad de la informaci´on de
partida en ambos m´etodos. En nuestro caso particular calcularemos primero
las posiciones de los receptores (al inducir ´estas una mayor incertidumbre
en el sistema), y luego aproximaremos los errores de los relojes.
43

44. No
1. H = δri1k
δxref
Error del reloj
1. H = δbn1
δbx
2. K = P·HT
H·P·HT +Σ
2. K = PHT
HPHT +Σ
3. h(bx) = H · bx
4. bx
(+)
= bx
(−)
+ K z − h(b(−)
x )
Posici´on real de la referencias
3.h(xref )=|xreci−xek|−|xrec1−xek|
4.xref
(+)=x
(−)
ref
+K z−h(xref
(−)
)
P(+)=P(−)−K·H·P(−) P(+)
= P(−)
− K · H · P(−)
S´i
FILTRO DE INICIALIZACI´ON
Convergencia?
10.6 Resoluci´on conjunta de la inicializaci´on
El problema de la sincronizaci´on de los relojes de los receptores se puede
abordar desde otra perspectiva. En los puntos anteriores se enfoc´o el proble-
ma mediante la reducci´on de un error bi asociado a cada receptor, que afecta
doblemente a cada una de las medidas tomadas hi1k = oi1k +bi −b1. De esta
manera se obtiene una sincronizaci´on de los relojes lo m´as aproximada posi-
ble a la base de tiempo real. Sin embargo, se puede aumentar la precisi´on
del sistema sincronizando los relojes de los receptores respecto a la base de
tiempo ”err´onea” de uno de ellos.
Sea t la base de tiempo real del sistema y b1 el error desconocido del
reloj del receptor 1. Desplazando la base de tiempo del sistema a t + b1,
el nuevo error del reloj del receptor i, bi1, ser´a igual a la diferencia entre
las observaciones esperadas y las observaciones obtenidas bi1 = hi1k − oi1k.
Para el caso en el que la posici´on de los puntos de referencia fuera exacta,
se puede lograr la sincronizaci´on de los relojes de los receptores empleando
44

45. un ´unico emisor de referencia.
Para la resoluci´on conjunta del problema de las posiciones reales de los
puntos de referencia y la sincronizaci´on, a˜nadimos la inc´ognita bi1 al prob-
lema de las posiciones reales. Obtenemos por tanto el siguiente sistema de
ecuaciones
ri1k = xreci − xek − xrec1 − xek + bi1. (96)
Como primer paso se define el vector de estado x, formado por las posi-
ciones de referencia, xref , y por los errores del reloj, bi1 : x = (xref , bi1).
A continuaci´on se calcula la matriz Jacobiana H del sistema de ecuaciones
rijk, (o matriz de sensibilidad a las observaciones) sobre el vector de estado
H =
∂ri1k
∂x
. (97)
Como segundo paso se calcula la matriz de ganancia para poder pon-
derar el peso de cada conjunto nuevo de observaciones respecto al valor ya
estimado
K =
P · HT
H · P · HT + Σ
(98)
El tercer paso consiste en calcular el vector de observaciones esperado,
aplicando la funci´on no lineal h(x) al vector de estado estimado hasta el
momento. Esta funci´on no es otra que el propio sistema de ecuaciones rijk.
Aplicamos por tanto
h(xref ) = xreci − xek − xrec1 − xek + ˜bi1 (99)
donde bi1 corresponde a la estimaci´on actual del error de sincronizaci´on
del receptor i respecto del receptor 1.
A continuaci´on utilizamos el vector de observaciones esperado h(x), el
vector de observaciones obtenido z y la matriz de ganancia K para estimar
el nuevo vector de estado x. Igualmente utilizaremos la matriz de ganancia
K y la matriz de sensibilidad a las observaciones H para actualizar la matriz
de covarianza del proceso P.
x(+)
= x(−)
+ K z − h(x(−)
) (100)
P(+)
= P(−)
− K · H · P (101)
45

46. Finalmente realizaremos un test de convergencia, y en caso de no cumplir-
lo volveremos al primer paso utilizando el nuevo vector de estado. Como
criterio de convergencia Critconv podemos utilizar la distancia entre los vec-
tores de estado a priori y a posteriori.
Critconv → x(+)
− x(−)
≤ (102)
10.7 Supervisi´on de receptores no est´aticos
Una vez resuelta la inicializaci´on del sistema se puede utilizar el conjun-
to de receptores para posicionar los chips emisores. Algunos de los recep-
tores podr´ıan estar situados sobre plataformas sujetas a oscilaciones o ligeros
movimientos. ´Este ser´ıa el caso de un receptor colocado sobre un m´astil de
20 metros de altura. Por una parte, la mayor diferencia de altura respecto
a la posici´on de los emisores asegura una mayor precisi´on en la componente
vertical de la posici´on. Por otra parte, el viento podr´ıa hacer oscilar el m´astil,
introduciendo un error adicional en el sistema.
Se define el vector de estado del receptor q a partir de su posici´on sobre
un sistema de coordenadas cartesianas, x = (x, y, z). Sea x0 su posici´on
te´orica, y riqk el conjunto de observaciones de diferencias de distancias del
emisor de referencia k a los receptores q e i, tales que i = 1, 2, ...n, con i = q.
Se puede estimar la posici´on de los receptores utilizando el siguiente filtro
de Kalman.
Como primer paso se calcula la matriz Jacobiana H del sistema de ecua-
ciones riqk (o matriz de sensibilidad a las observaciones) sobre el vector de
estado
H =
∂riqk
∂x
(103)
El segundo paso consiste en calcular la matriz de ganancia.
K =
P · HT
H · P · HT + Σ
(104)
donde Σ representa la matriz de covarianza de las medidas conocidas, y P
la matriz de covarianza del proceso (o del vector de estado bx ).
Se define el vector de observaciones esperado
h(x) = xreci − xek − xrecq − xek , i = 1, · · · n, i = q. (105)
46

47. Para estimar el nuevo vector de estado x se utiliza el vector de obser-
vaciones esperado h(x), el vector de observaciones obtenido z y la matriz
de ganancia K. La matriz de covarianza del proceso P se puede calcular
a partir de la matriz de ganancia K y de la matriz de sensibilidad a las
observaciones H.
ˆx
(+)
k−1 = x
(−)
k−1 + K z − h(x(−)
) (106)
P
(+)
k−1 = P(−)
− K · H · P (107)
La ”Actualizaci´on del estado por predicci´on”, se realiza a partir del mod-
elo din´amico que se aplique. En el caso del receptor situado sobre un m´astil
para ganar altura, las variaciones en la posici´on del receptor seguir´an el
modelo de movimiento representado en la gr´afica siguiente
88
89
90
91
92 −69
−68
−67
−66
−65
0
5
10
15
20
25
30
35
40
Modelo din’amico de un receptor situado sobre un m’astil
Figura 14: Modelo Din´amico Receptor sobre M´astil
El modelo din´amico se puede representar como funci´on de desplazamien-
to a lo largo de una regi´on de la esfera con centro en la base del m´astil y
radio la altura del receptor. Sea ˆγ
(+)
k−1 la posici´on del receptor en coordenadas
esf´ericas obtenida a partir de la transformaci´on de coordenadas de ˆx
(+)
k−1
ˆx
(+)
k−1 → ˆγ
(+)
k−1
(x
(+)
k−1, y
(+)
k−1, z
(+)
k−1, ˙x
(+)
k−1, ˙y
(+)
k−1, ˙z
(+)
k−1) → (θ
(+)
k−1, λ
(+)
k−1, ˙θ
(+)
k−1, ˙λ
(+)
k−1).
Se definen ˙θ
(+)
k−1 y ˙λ
(+)
k−1 como las variaciones en los ´angulos λ y θ a lo
largo del intervalo de tiempo ∆t = (tk−2, tk−1), o velocidades angulares en
tk−1
47

48. ˙θ
(+)
k−1 =
θ
(+)
k−1 − θ
(+)
k−2
∆t
(108)
˙λ
(+)
k−1 =
λ
(+)
k−1 − λ
(+)
k−2
∆t
. (109)
Es posible predecir el estado ˆγ
(−)
k de γ en el momento tk, utilizando el
modelo din´amico ϕk definido a partir de (108) y (109).
ϕk =





1 0 ∆t 0
0 1 0 ∆t
0 0 1 0
0 0 0 1





.
La ”Actualizaci´on del estado por predicci´on” se lleva a cabo primero
en coordenadas esf´ericas, y luego ´estas se transforman al sistema cartesiano
empleado normalmente por el sistema ˆx
(−)
k
ˆγ
(−)
k = ϕk · ˆγ
(+)
k−1 (110)
ˆγ
(−)
k → ˆx
(−)
k .
Para la actualizaci´on de la matriz de covarianzas P
(−)
k se aplica primero
al modelo din´amico la transformaci´on de coordenadas esf´ericas a cartesianas.
Asimismo se ha de a˜nadir la covarianza de ruido din’amico Qk−1.
ϕk → Φk
P
(−)
k = ΦkP
(+)
k−1ΦT
k + Qk−1. (111)
Existen otras estructuras f´ısicas sobre las que se pueden colocar los re-
ceptores que pueden producir variaciones diferentes en la posici´on de los
mismos. De esta manera, un receptor situado sobre un tejado est´a sujeto a
variaciones en la posici´on en forma de ”arco”, como viene representado por
la gr´afica de la Figura 6.
El modelo din´amico se puede representar como funci´on de desplazamien-
to a lo largo de un arco del c´ırculo con centro en la base del tejado y radio
la distancia entre la base y la posici´on del receptor. Sea ˆγ
(+)
k−1 la posici´on del
receptor en coordenadas circulares obtenida a partir de la transformaci´on
de coordenadas de ˆx
(+)
k−1
ˆx
(+)
k−1 → ˆγ
(+)
k−1
48

49. 0 5 10 15 20 0
10
20
30−8
−6
−4
−2
0
2
4
6
8
Modelo din’amico de un receptor situado sobre un tejado
Figura 15: Modelo Dinamico Receptor sobre un Tejado
(x
(+)
k−1, y
(+)
k−1, z
(+)
k−1, ˙x
(+)
k−1, ˙y
(+)
k−1, ˙z
(+)
k−1) → (ω
(+)
k−1, ˙ω
(+)
k−1).
Se define ˙ω
(+)
k−1 como la velocidad angular del receptor en el momento
tk−1, y se utiliza para construir el modelo din´amico.
˙ω
(+)
k−1 =
ω
(+)
k−1 − ω
(+)
k−2
∆t
ϕk =
1 ∆t
0 1
La ”Actualizaci´on del estado por predicci´on” se lleva a cabo primero en
coordenadas circulares, y luego ´estas se transforman al sistema cartesiano
empleado normalmente por el sistema ˆx
(−)
k .
ˆγ
(−)
k = ϕk · ˆγ
(+)
k−1 (112)
ˆγ
(−)
k → ˆx
(−)
k
Para la actualizaci´on de la matriz de covarianzas P
(−)
k se aplica primero
al modelo din´amico la transformaci´on de coordenadas circulares a carte-
sianas. Asimismo, se ha de sumar la covarianza de ruido din’amico Qk−1.
ϕk → Φk
P
(−)
k = ΦkP
(+)
k−1ΦT
k + Qk−1. (113)
49

50. Referencias
[1] https://gps.losangeles.af.mil/
[2] http://www.glonass-center.ru/
[3] http://www.esa.int/esaNA/galileo.html
[4] http://www.esa.int/esaNA/egnos.html
[5] http://waas.stanford.edu/research/waas.htm
[6] http://www.ista.jaxa.jp/eng/newsletter/2003summer/3.html
[7] http://www.cenc.org.cn/en/
[8] H. Contreras ”Hector Contreras ”GPS+GLONASS Technology at
Chuquicamata Mine, Chile” ION GPS-98 11th International Technical
Meeting of the Satellite Division of the Institute of Navigation. 1998.
[9] M. Grewal ”Global Positioning Systems, Inertial Navigation, and Inte-
gration” John Wiley & Sons, Inc. 2001
[10] B. Hofmann-Wellenhof, H. Lichtenegger, J. Collins: ”GPS Theory and
Practice.” Springer Wien New York. Fifth Edition 2001.
[11] http://www.navcen.uscg.gov/Ftp/gps/status.txt
[12] http://www.glonass-center.ru/nagu.html
[13] GPS Navstar JPO Interface Control Document GPS ICD-GPS-200. ”
Revisi´on C IRN-200C-004 12 Abril 2000
[14] Federaci´on Rusa, Ministerio de Defensa ”GLONASS Interface Control
Document.” Quinta Versi´on 2002
[15] D. Brower, G. Clemence: ”Methods of Celestial Mechanics.” Academic
Press New York 1961.
[16] National Imaginery and Mapping Agency: ”Departament of Defense
World Geodetic System 1984” Terceras Edici´on 1997
[17] V. Mitrikas, S.G. Revnivykh, and E.V. Bykhanov: WGS84/PZ90 trans-
formation parameters determination based on laser and ephemeris long-
term GLONASS orbital data processing. Proceedings of ION-GPS 98,
the Institute of Navigation, Part II, pp. 1625-1635.
[18] J. Klobuchar. ”Ionospheric Time Delay Corrections for Advanced Satel-
lite Ranging Systems.” NATO AGARD Procedimientos de la Conferen-
cia n 209, sobre Limitaciones de Propagaci´on de Sistemas de Navegaci´on
y Posicionamiento. NATO AGARD, Paris 1976.
50

51. [19] H. Hopfield. ”Two quartic tropospheric refractivity profile for correcting
satellite data.” Journal of Geophysical Research, 74 (18): 4487-4499
1969.
[20] J. Saastamoinen. ”Contribution to the Theory of Atmospheric Refrac-
tion.” Bulletin G´eod´esique, 107:13-34 1973.
[21] K.C. Ho, Y.T. Chan: ”Solution and performance analysis of Geolocation
by TDOA.” IEEE Transactions on Aerospace and Electronic Systems
Vol. 29, No. 4 Octubre 1993
[22] B. T. Fang.: ”Simple Solutions for Hyperbolic and Related Position Fix-
es.” IEEE Transactions on Aerospace and Electronic Systems Vol. 26,
No. 5 Septiembre 1990
[23] S. Bancroft: ”An Algebraic Solution of the GPS Equations.” IEEE
Transactions on Aerospace and Electronic Systems Vol. AES-25, No.
7 Enero 1985
[24] R. E. Kalman: ”A new Approach to Linear Filtering and Prediction
Problems.” Transactions of the ASME - Journal of Basic Engineering
82 (Series D): 35-45 1960
[25] Werner Gurtner: ”RINEX The Receiver Independent Exchange For-
mat.” Version 2.10, May 5 th 2000. Astronomical Institute University
of Berne.
[26] http://www2.ocgy.ubc.ca/ rich/map.html
51