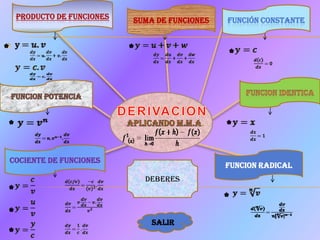
El documento habla sobre los conceptos básicos de derivadas, incluyendo la derivada de funciones como productos, sumas, constantes, potencias, identidades, cocientes y radicales. Explica las fórmulas para derivar cada tipo de función y provee ejemplos numéricos.