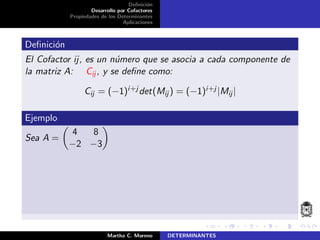
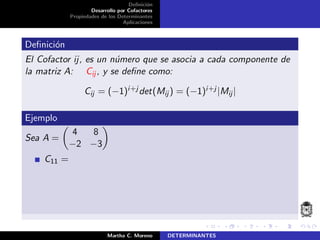
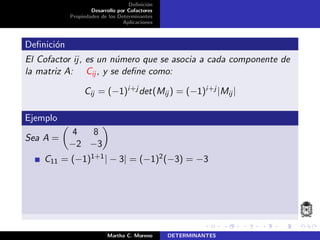
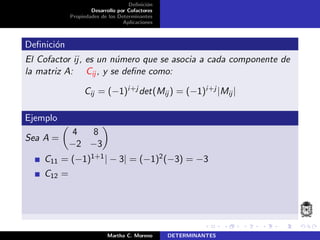
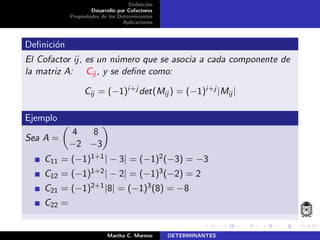
El documento describe la definición de determinantes, su cálculo mediante el desarrollo por cofactores y las propiedades asociadas. Se plantea un método de recurrencia para calcular el determinante de matrices cuadradas, donde el determinante de una matriz de tamaño n × n se calcula a partir de matrices de tamaño n − 1 × n − 1. Adicionalmente, se introducen conceptos como los menores y cofactores, que son esenciales para el cálculo de determinantes.
















































































































































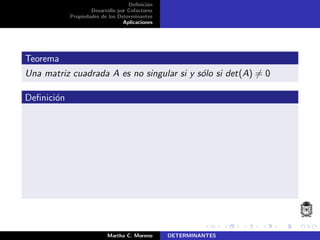




























![Definici´on
Desarrollo por Cofactores
Propiedades de los Determinantes
Aplicaciones
xi = 1
det(A) [c1i b1 + c2i b2 + . . . + cni bn]
Martha C. Moreno DETERMINANTES](https://image.slidesharecdn.com/determinantes-160403030739/85/Determinantes-algebra-lineal-191-320.jpg)
![Definici´on
Desarrollo por Cofactores
Propiedades de los Determinantes
Aplicaciones
xi = 1
det(A) [c1i b1 + c2i b2 + . . . + cni bn]
xi = 1
det(A)
Martha C. Moreno DETERMINANTES](https://image.slidesharecdn.com/determinantes-160403030739/85/Determinantes-algebra-lineal-192-320.jpg)
![Definici´on
Desarrollo por Cofactores
Propiedades de los Determinantes
Aplicaciones
xi = 1
det(A) [c1i b1 + c2i b2 + . . . + cni bn]
xi = 1
det(A)
a11 . . . a1i−1 b1 a1i+1 . . . a1n
a21 . . . a2i−1 b2 a2i+1 . . . a2n
. . . . . . . . . . . .
an1 . . . ani−1 bn ani+1 . . . ann
Martha C. Moreno DETERMINANTES](https://image.slidesharecdn.com/determinantes-160403030739/85/Determinantes-algebra-lineal-193-320.jpg)
![Definici´on
Desarrollo por Cofactores
Propiedades de los Determinantes
Aplicaciones
xi = 1
det(A) [c1i b1 + c2i b2 + . . . + cni bn]
xi = 1
det(A)
a11 . . . a1i−1 b1 a1i+1 . . . a1n
a21 . . . a2i−1 b2 a2i+1 . . . a2n
. . . . . . . . . . . .
an1 . . . ani−1 bn ani+1 . . . ann
xi =
Martha C. Moreno DETERMINANTES](https://image.slidesharecdn.com/determinantes-160403030739/85/Determinantes-algebra-lineal-194-320.jpg)
![Definici´on
Desarrollo por Cofactores
Propiedades de los Determinantes
Aplicaciones
xi = 1
det(A) [c1i b1 + c2i b2 + . . . + cni bn]
xi = 1
det(A)
a11 . . . a1i−1 b1 a1i+1 . . . a1n
a21 . . . a2i−1 b2 a2i+1 . . . a2n
. . . . . . . . . . . .
an1 . . . ani−1 bn ani+1 . . . ann
xi = det(Ai )
det(A)
Martha C. Moreno DETERMINANTES](https://image.slidesharecdn.com/determinantes-160403030739/85/Determinantes-algebra-lineal-195-320.jpg)
![Definici´on
Desarrollo por Cofactores
Propiedades de los Determinantes
Aplicaciones
xi = 1
det(A) [c1i b1 + c2i b2 + . . . + cni bn]
xi = 1
det(A)
a11 . . . a1i−1 b1 a1i+1 . . . a1n
a21 . . . a2i−1 b2 a2i+1 . . . a2n
. . . . . . . . . . . .
an1 . . . ani−1 bn ani+1 . . . ann
xi = det(Ai )
det(A)
Donde Ai es la matriz que se obtiene de A reemplazando la
columna i por B
Martha C. Moreno DETERMINANTES](https://image.slidesharecdn.com/determinantes-160403030739/85/Determinantes-algebra-lineal-196-320.jpg)