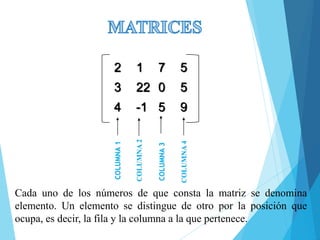
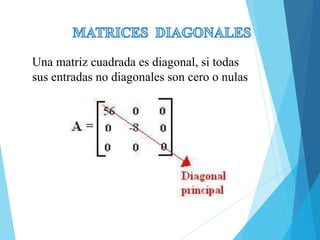
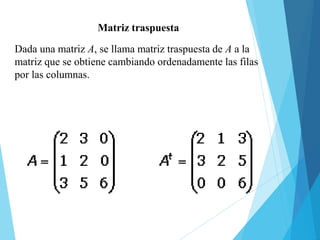
Este documento presenta conceptos básicos sobre matrices, incluyendo su definición, elementos, dimensiones, tipos como cuadradas y diagonales, operaciones como suma, resta, multiplicación por escalar, y determinantes. También cubre la multiplicación de matrices y algunas de sus propiedades como asociatividad y distributividad.

1. UNIVERSIDAD CENTRAL DEL ECUADOR
FACULTAD DE INGENIERÍA QUÍMICA
CURSO DE NIVELACIÓN DE CARRERA
OPERACIONES CON MATRICES Y DETERMINANTES
MATEMÁTICAS
PROFESOR: Ing. Jorge López
PERIODO: Abril-Septiembre 2014
QUITO – ECUADOR

2. Se denomina matriz a todo conjunto de números o
expresiones dispuestos en forma rectangular, formando
filas y columnas.
2 1 7 5
3 22 0 5
4 -1 5 9
Fila 2
Fila 2
Fila 2
LAS FILAS SE CUENTAN DESDE
ARRIBA PARAABAJO

3. 2 1 7 5
3 22 0 5
4 -1 5 9
COLUMNA1
COLUMNA2
COLUMNA3
COLUMNA4
Cada uno de los números de que consta la matriz se denomina
elemento. Un elemento se distingue de otro por la posición que
ocupa, es decir, la fila y la columna a la que pertenece.

4. Una matriz con m filas y n columnas es una matriz m x n o es
de dimensión m x n
2 1 7 5
3 22 0 5
4 -1 5 9
Una matriz con n filas y n columnas es una matriz cuadrada
de dimensión n x n
0 2 4
-4 -8 1
3 X 4
2 X 2

5. Una matriz cuadrada es diagonal, si todas
sus entradas no diagonales son cero o nulas

6. Dada una matriz A, se llama matriz traspuesta de A a la
matriz que se obtiene cambiando ordenadamente las filas
por las columnas.
Matriz traspuesta

7. La suma de dos matrices de orden m x n es otra matriz
dimensión m x n.
A + (B + C) = (A + B) + CAsociativa
Elemento neutro: A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
Elemento opuesto A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de
signo.
Conmutativa A + B = B + A

8. 8 -4 0
1 2 -1
5 2
-1 -3 -1
4
58 + 4-4 + 20 +
-11 + -32 + -1-1 +
A + B =
A = B =
13 0 2
0 -1 -2
A + B =

9. La resta de matrices consiste en restar las entradas que
son correspondientes.
8 -4 0
1 2 -1
5 2
-1 -3 -1
4
58 - 4-4 - 20 -
(-1)1 - (-3)2 - (-1)-1 -
A = B =
A - B =
3 -8 -2
2 5 0A - B =

10. Ejemplo combinado (suma y resta)

11. La multiplicación de un escalar por una matriz
consiste en multiplicar el escalar por cada una de las
entradas de la matriz.
Un escalar es un número real, constante o complejo
que sirve para describir un fenómeno físico con
magnitud, pero sin dirección.
8 -4 0
1 2 -1
7 ×
35 -28 0
7 14 -7
=

12. La multiplicación de matrices es un proceso diferente a las
operaciones estudiadas hasta el momento. Para entender de mejor
manera la multiplicación entre matrices, primero vamos a definir la
multiplicación de una fila por una columna.
Multiplicación de una fila por una columna
Si A es una matriz m × n y B es una matriz n × k , podemos hallar
la multiplicación de la fila i de A por la columna j de B, de la
siguiente manera:
Multiplicar la primera fila de A por la segunda columna de B
1 0 3
2 -1 -2
8 -42
1 2 -1
1 11
A B

13. SOLUCIÓN
1 0
2 -1 -2
2 38 -4
1 2 -1
1 11
A =
B =
(1 × -4) + (0 × 2) + (2× 1) = -2

14. Dos matrices A y B son multiplicables si el
número de columnas de A coincide con el
número de filas de B.
Mm x n x Mn x p = M m x p
El elemento cij de la matriz producto se obtiene
multiplicando cada elemento de la fila i de la
matriz A por cada elemento de la columna j de
la matriz B y sumándolos.

15. EJEMPLO:

16. • Asociativa:
A · (B · C) = (A · B) · C
• Elemento neutro:
A · I = A
Donde I es la matriz identidad del mismo orden
que la matriz A.
• No es Conmutativa:
A · B ≠ B · A
• Distributiva del producto respecto de la
suma:
A · (B + C) = A · B + A · C

17. La división de matrices se define como el producto del
numerador multiplicado por la matriz inversa del
denominador.
Es decir, sean las matrices A y B tal que A/B = AB-1:
Si una matriz está dividida entre un escalar, todos los
términos de la matriz quedarán divididos por ese escalar.

18. A cada matriz cuadrada A se le asigna un escalar particular
denominado determinante de A, denotado por |A| o por det (A).
|A| =

19. Determinante de orden uno
|a11| = a11
Ejemplo: |5| = 5
Determinante de orden dos
Ejemplo:

20. = a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 −
− a13 a22 a31 − a12 a21 a 33 − a11 a23 a32.
Consideremos una matriz 3x3 arbitraria A = (aij).
El determinante de A se define como sigue:
Determinante de orden tres

21. 3 · 2 · 4 + 2 · (−5) · (−2) + 1 · 0 · 1 −
− 1 · 2 · (−2) − 2 · 0 · 4 − 3 · (−5) · 1 =
= 24 + 20 + 0 − (−4) − 0 − (−15) =
= 44 + 4 + 15 = 63
EJEMPLO: