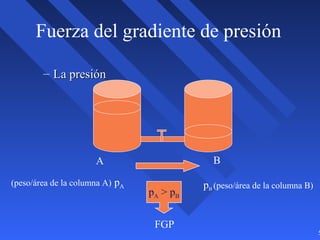
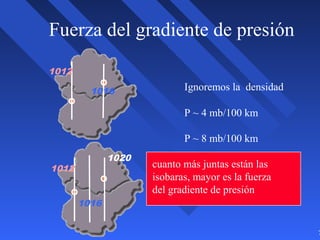
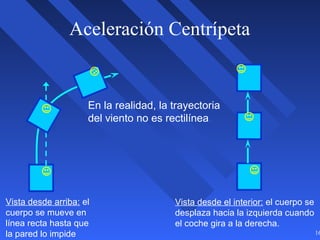
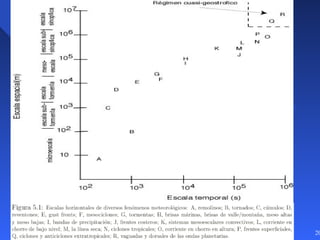
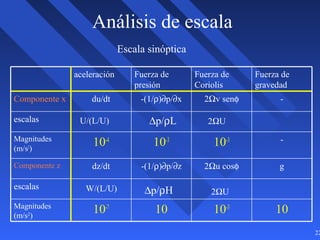
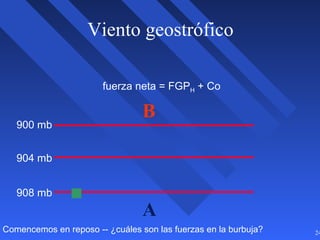
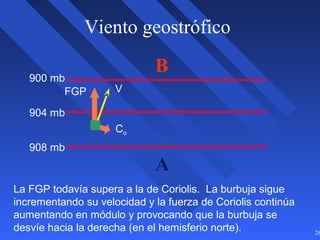
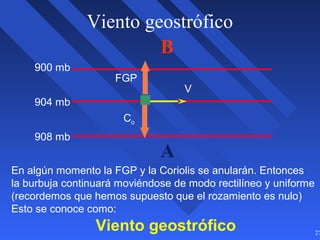
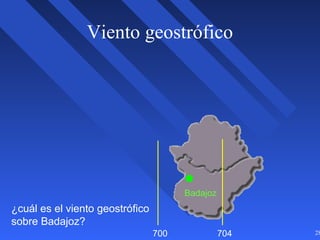
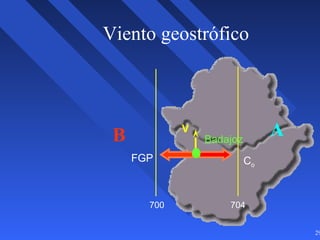
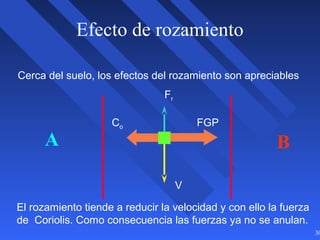
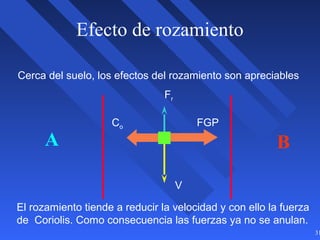
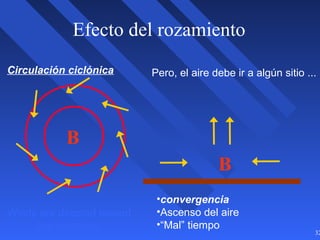
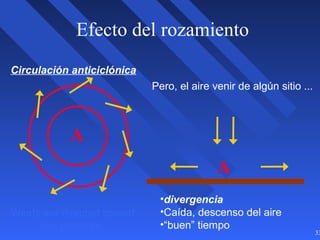
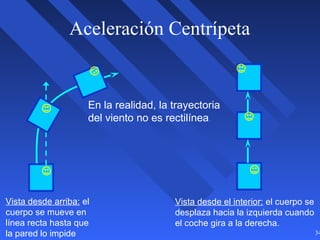
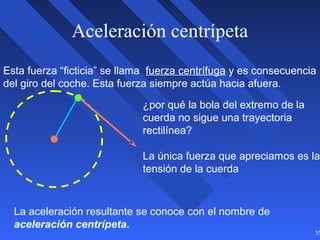
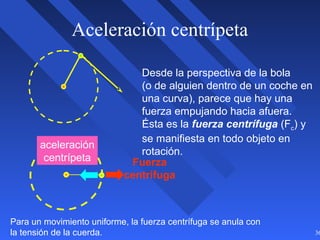
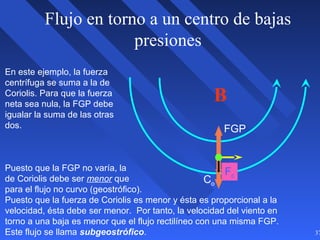
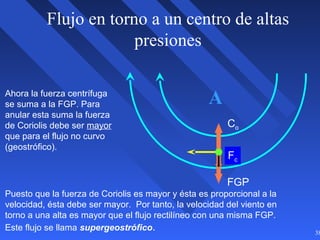
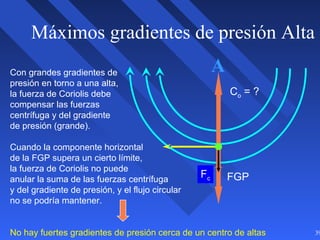
Este documento introduce los conceptos básicos de la dinámica atmosférica, incluyendo las fuerzas que afectan el movimiento del aire como la gravedad, el gradiente de presión y la fuerza de Coriolis. También explica cómo el equilibrio entre estas fuerzas da lugar a los vientos geostróficos y cómo el rozamiento afecta los patrones de viento cerca de la superficie.

1. 1
INTRODUCCIÓN A LA
DINÍMICA ATMOSFÉRICA

2. 2
Objetivo de la dinámica:
El estudio del movimiento del aire en la
atmósfera, sus causas y evolución futura.
Constituye la base teórica de la predicción del
tiempo atmosférico

3. 3
Ecuaciones del movimiento:
– Ley de NewtonLey de Newton
m ⋅
r
a =
r
F

4. 4
Tipos de Fuerza
Tipos de fuerza en la atmósfera
– El peso (gravedad)El peso (gravedad)
Gravedad
- mg

5. 5
Fuerza del gradiente de presión
– La presiónLa presión
(peso/área de la columna A) pA
A
pB (peso/área de la columna B)
B
pA > pB
FGP

6. 6
Fuerza del gradiente de presión
Fuerza del gradiente de presión
Tiene aplicación a los mapas del tiempo..............
1012
1014
FGP = - (1/ρ) (∆p/∆n)*
ρ es la densidad del aire
∆ p es la diferencia de presión
∆ n es la distancia entre los
observatorios
* (por unidad de masa)

7. 7
Ignoremos la densidad
P ~ 4 mb/100 km
P ~ 8 mb/100 km
cuanto más juntas están las
isobaras, mayor es la fuerza
del gradiente de presión
Fuerza del gradiente de presión
1012
1016
1012
1020
1016

8. 8
Como es un vector, la fuerza de gradiente
de presión tiene 3 componentes: 2 en el
plano horizontal y una en la vertical:
FGPFGPxx = -(1/= -(1/ρρ) () (∆∆p/p/∆∆x)x)
FGPFGPyy = -(1/= -(1/ρρ) () (∆∆p/p/∆∆y)y)
FGPFGPzz = -(1/= -(1/ρρ) () (∆∆p/p/∆∆z)z)
Como ya se vio en su momento en condiciones de equilibrio hidrostático
FGPz = -g. Ecuación válida en procesos a gran escala
Fuerza del gradiente de presión

9. 9
¿Como se mueve la pelota ?: En línea recta o curva
Fuerzas no inerciales
Fuerza de Coriolis

10. 10
Fuerzas no inerciales: fuerza de Coriolis
Si has dicho línea curva: Es que hay una fuerza que hace
que la trayectoria se curve: La fuerza de Coriolis
¿A que se debe ?: Pues a que el experimento lo hacemos
en un sistema en rotación => Es un sistema no inercial.
Nosotros vemos moverse al aire desde un sistema no
inercial: La tierra en rotación respecto del eje polar, y por
tanto necesitamos introducir en las ecuaciones del
movimiento la fuerza de Coriolis

11. 11
Fuerzas no inerciales: fuerza de Coriolis
La Tierra gira con una velocidad Ω = 2π
radianes en 86400 segundos respecto del eje
polar. Desde el punto de vista de un
observador situado a una latitud φ la tierra
aparentemente gira con una velocidad Ω seno
φ. De tal forma que en el ecuador (φ=0, seno
φ = 0) la velocidad de rotación aparente es
cero y en el polo Ω (φ =π/2, seno π/2=1)

12. 12
Fuerzas no inerciales: fuerza de Coriolis
Hemos visto que la mesa se mueve en el sentido de las agujas del
reloj y que la pelota se mueve hacia la izquierda respecto de la
dirección en que es lanzada
La tierra gira en sentido contrario a las agujas del reloj (en el
hemisferio norte) y por tanto la fuerza de Coriolis actúa hacia la
derecha en dicho hemisferio:

13. 13
Fuerzas no inerciales: fuerza de Coriolis
Que pasa con una globo que lanzamos desde Badajoz, que
está a una latitud f. Según hemos dicho antes para un
observador situado en Badajoz, la tierra gira
aparentemente(respecto de la vertical del lugar) con una
velocidad angular Ω seno(φ). Así pues es como si
estuviésemos sentados en una mesa que gira con una
velocidad angular más baja que en el polo, pero que de
todas formas gira. Por lo que el globo tenderá a virar hacia
la derecha, independientemente de la dirección horizontal
en la que se lance. ¿Que pasa si estamos en el Ecuador ?

14. 14
Fuerzas no inerciales: fuerza de Coriolis
Para que aparezca la fuerza de Coriolis es
necesario que el aire se mueva respecto de la
Tierra (al igual que lo hace la pelota en el
tiovivo). Esto es la velocidad relativa del aire
debe de ser distinta de cero. Se puede ver
que la fuerza de Coriolis vale por unidad de
masa (módulo):
FC = -2FC = -2 ΩΩ seno (seno (φ)φ) vv
Siendo v la velocidad relativaSiendo v la velocidad relativa
ρ
FC = −2(
r
Ω ×
r
v)

15. 15
Fuerzas no inerciales: fuerza Centrífuga
Esta fuerza la hemos notado todo el mundo.
Basta que montemos en autobus. Que pasa
al entrar en la rotonda un poco deprisa. Pues
tendemos a irnos hacia el lado contrario
respecto a la dirección en la que vira el
autobus: Es la fuerza centrifuga. Esta
misma fuerza centrifuga la sentimos cuando
gira la tierra respecto de su eje de rotación.
Es la responsable de la forma achatada de la
Tierra.

16. 16
Aceleración Centrípeta
En la realidad, la trayectoria
del viento no es rectilínea.
Vista desde arriba: el
cuerpo se mueve en
línea recta hasta que
la pared lo impide
Vista desde el interior: el cuerpo se
desplaza hacia la izquierda cuando
el coche gira a la derecha.

17. 17
Rozamiento
Además de las fuerzas que acabamos de
ver, practicámente todos los objetos que se
mueven sufren algún tipo de rozamiento. Lo
mismo le pasa al aire. Al moverse respecto
del suelo sufre rozamiento con el mismo.
Lo mismo sucede cuando algunas capas de
aire se mueven unas respecto de las otras.
El mayor rozamiento se da cerca del suelo,
debido a la presencia de éste.

18. 18
Juntando todas las fuerzas tenemos:
F = FGP + FCO + FCE + FR+GF = FGP + FCO + FCE + FR+G
y la ecuación de Newton resulta ser
a = FGP + FCO + FCE + FR+G
d
r
v
dt
= −
1
ρ
∇ p − 2(
r
Ω ×
r
v) −
r
Ω × (
r
Ω ×
r
r) − g
r
k +
r
Fr

19. 19
Análisis de escala

20. 20

21. 21
Escala sinóptica

22. 22
Análisis de escala
1010-3
1010-7Magnitudes
(m/s2
)
escalas
g2Ωu cosφ-(1/ρ)∂p/∂zdz/dtComponente z
-10-3
10-3
10-4Magnitudes
(m/s2
)
escalas
-2Ωv senφ-(1/ρ)∂p/∂xdu/dtComponente x
Fuerza de
gravedad
Fuerza de
Coriolis
Fuerza de
presión
aceleración
U/(L/U) 2ΩU∆p/ρL
W/(L/U) ∆p/ρH 2ΩU
Escala sinóptica

23. 23
Análisis de escala
A escala sinóptica:
– Equilibrio entre la fuerza horizontal delEquilibrio entre la fuerza horizontal del
gradiente de presión y la fuerza de Coriolis =>gradiente de presión y la fuerza de Coriolis =>
Atmósfera geostróficaAtmósfera geostrófica
– Equilibrio entre la componente vertical delEquilibrio entre la componente vertical del
gradiente de presión y la gravedad =>gradiente de presión y la gravedad =>
Atmósfera hidrostáticaAtmósfera hidrostática
Ro =
U
fL
<<1

24. 24
Viento geostrófico
fuerza neta = FGPH + Co
B
A
900 mb
904 mb
908 mb
Comencemos en reposo -- ¿cuáles son las fuerzas en la burbuja?

25. 25
Viento geostrófico
B
A
900 mb
904 mb
908 mb
FGP
Inicialmente la fuerza de Coriolis es nula, pero al comenzar a
ascender la burbuja, la fuerza de Coriolis deja de ser nula. Al
aumentar la velocidad de la burbuja aumenta la fuerza de Coriolis.

26. 26
Viento geostrófico
B
A
900 mb
904 mb
908 mb
FGP
Co
V
La FGP todavía supera a la de Coriolis. La burbuja sigue
incrementando su velocidad y la fuerza de Coriolis continúa
aumentando en módulo y provocando que la burbuja se
desvíe hacia la derecha (en el hemisferio norte).

27. 27
Viento geostrófico
B
A
900 mb
904 mb
908 mb
FGP
Co
V
En algún momento la FGP y la Coriolis se anularán. Entonces
la burbuja continuará moviéndose de modo rectilíneo y uniforme
(recordemos que hemos supuesto que el rozamiento es nulo)
Esto se conoce como:
Viento geostrófico

28. 28
Viento geostrófico
700 704
¿cuál es el viento geostrófico
sobre Badajoz?
Badajoz

29. 29
Viento geostrófico
700 704
Badajoz
Co
FGP
V AB

30. 30
Efecto de rozamiento
Cerca del suelo, los efectos del rozamiento son apreciables
A B
FGPCo
V
Fr
El rozamiento tiende a reducir la velocidad y con ello la fuerza
de Coriolis. Como consecuencia las fuerzas ya no se anulan.

31. 31
Efecto de rozamiento
Cerca del suelo, los efectos del rozamiento son apreciables
A B
FGPCo
V
Fr
El rozamiento tiende a reducir la velocidad y con ello la fuerza
de Coriolis. Como consecuencia las fuerzas ya no se anulan.

32. 32
Efecto del rozamiento
B
Winds are directed toward
low pressure.
Pero, el aire debe ir a algún sitio ...
B
•convergencia
•Ascenso del aire
•“Mal” tiempo
Circulación ciclónica

33. 33
Efecto del rozamiento
Winds are directed toward
low pressure.
•divergencia
•Caída, descenso del aire
•“buen” tiempo
Circulación anticiclónica
A
A
Pero, el aire venir de algún sitio ...

34. 34
Aceleración Centrípeta
En la realidad, la trayectoria
del viento no es rectilínea.
Vista desde arriba: el
cuerpo se mueve en
línea recta hasta que
la pared lo impide
Vista desde el interior: el cuerpo se
desplaza hacia la izquierda cuando
el coche gira a la derecha.

35. 35
Aceleración centrípeta
Esta fuerza “ficticia” se llama fuerza centrífuga y es consecuencia
del giro del coche. Esta fuerza siempre actúa hacia afuera.
¿por qué la bola del extremo de la
cuerda no sigue una trayectoria
rectilínea?
La única fuerza que apreciamos es la
tensión de la cuerda
La aceleración resultante se conoce con el nombre de
aceleración centrípeta.

36. 36
Aceleración centrípeta
Desde la perspectiva de la bola
(o de alguien dentro de un coche en
una curva), parece que hay una
fuerza empujando hacia afuera.
Ésta es la fuerza centrífuga (Fc) y
se manifiesta en todo objeto en
rotación.
Fuerza
centrífuga
aceleración
centrípeta
Para un movimiento uniforme, la fuerza centrífuga se anula con
la tensión de la cuerda.

37. 37
En este ejemplo, la fuerza
centrífuga se suma a la de
Coriolis. Para que la fuerza
neta sea nula, la FGP debe
igualar la suma de las otras
dos.
Puesto que la FGP no varía, la
de Coriolis debe ser menor que
para el flujo no curvo (geostrófico).
Puesto que la fuerza de Coriolis es menor y ésta es proporcional a la
velocidad, ésta debe ser menor. Por tanto, la velocidad del viento en
torno a una baja es menor que el flujo rectilíneo con una misma FGP.
Este flujo se llama subgeostrófico.
Flujo en torno a un centro de bajas
presiones
B
FGP
Co
Fc

38. 38
Ahora la fuerza centrífuga
se suma a la FGP. Para
anular esta suma la fuerza
de Coriolis debe ser mayor
que para el flujo no curvo
(geostrófico).
Puesto que la fuerza de Coriolis es mayor y ésta es proporcional a la
velocidad, ésta debe ser mayor. Por tanto, la velocidad del viento en
torno a una alta es mayor que el flujo rectilíneo con una misma FGP.
Este flujo se llama supergeostrófico.
Flujo en torno a un centro de altas
presiones
FGP
Co
Fc
A

39. 39
Con grandes gradientes de
presión en torno a una alta,
la fuerza de Coriolis debe
compensar las fuerzas
centrífuga y del gradiente
de presión (grande).
Cuando la componente horizontal
de la FGP supera un cierto límite,
la fuerza de Coriolis no puede
anular la suma de las fuerzas centrífuga
y del gradiente de presión, y el flujo circular
no se podría mantener.
No hay fuertes gradientes de presión cerca de un centro de altas
Máximos gradientes de presión Alta
FGP
Co = ?
Fc
A

40. 40
Con grandes gradientes de
presión en torno a una alta,
las grandes FGP deben
anular las fuerzas centrífugas
y de Coriolis.
Teóricamente no hay límite para la
componente horizontal de la fuerza
del gradiente de presión, por lo que
ésta puede anular la suma de las
fuerzas centrífuga y de Coriolis y el
flujo circular podría mantenerse.
Puede haber fuertes gradientes de presión cerca de un centro de bajas
Máximos gradientes de presión Baja
FGP
Co
Fc
B

41. 41
Superficies de presión
Dibujo hipotético de una superficie de 500 mb

42. 42
Dorsal Vaguada