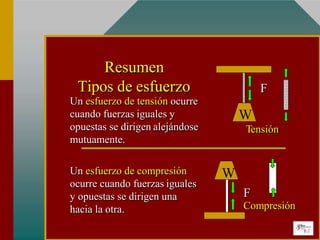
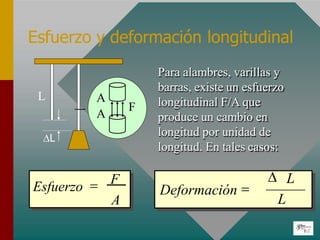
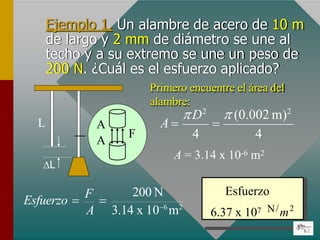
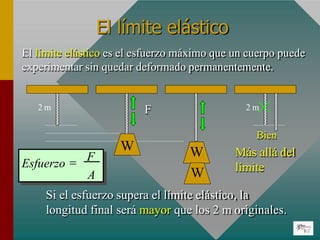
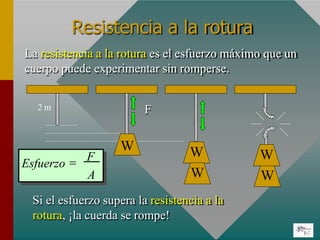
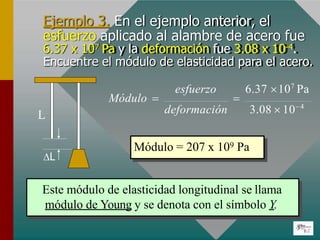
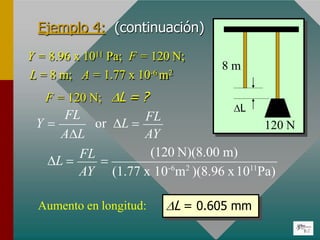
El documento describe las propiedades elásticas de los materiales y los conceptos de esfuerzo y deformación. Explica que el esfuerzo es la fuerza aplicada por unidad de área y la deformación es el cambio en longitud dividido por la longitud original. También define el límite elástico, la resistencia a la rotura y el módulo de Young, que relaciona el esfuerzo y la deformación de manera proporcional para materiales elásticos.

1. 2007

2. El salto BUNGEE utiliza
una larga cuerda
elástica que se estira
hasta que llega a una
longitud máxima que
es proporcional al peso
del saltador. La
elasticidad de la cuerda
determina la amplitud
de las oscilaciones
resultantes. Si se
excede el límite
elástico de la cuerda,
ésta se romperá.
Elasticidad

3. Propiedades elásticas de la materia
Un cuerpo elástico es aquel que regresa a su
forma original después de una deformación.
Bola de
golf
Balón de
fútbol
Banda de
goma

4. Propiedades elásticas de la materia
Un cuerpo inelástico es aquel que no regresa a su
forma original después de una deformación.
Masa o pan Barro Bola inelástica

5. Un resorte elástico
Un resorte es un ejemplo de un cuerpo elástico
que se puede deformar al estirarse.
Una fuerza restauradora,
F, actúa en la dirección
opuesta al desplazamiento
del cuerpo en oscilación.
F = -kx
x
F

6. Ley de Hooke
Cuando un resorte se estira, hay una fuerza
restauradora que es proporcional al
desplazamiento.
F = -kx
La constante de
resorte k es una
propiedad del resorte
dada por:
F
x
m
k 
F
x
La constante de resorte k es una
medida de la elasticidad del resorte.

7. Esfuerzo y deformación
x
F
Esfuerzo se refiere a la causa de una deformación, y
deformación se refiere al efecto de la deformación.
La fuerza descendente F
causa el desplazamiento x.
Por tanto, el esfuerzo es la
fuerza; la deformación es la
elongación.

8. Tipos de esfuerzo
Un esfuerzo de tensión ocurre
cuando fuerzas iguales y
opuestas se dirigen alejándose
mutuamente.
Un esfuerzo de compresión
ocurre cuando fuerzas
iguales y opuestas se dirigen
una hacia la otra.
F
W
Tensión
F
W
Compresión

9. Resumen de definiciones
Esfuerzo es la razón de una fuerza aplicada F
al área A sobre la queactúa:
Deformación es el cambio relativo en las dimensiones o
forma de un cuerpo como resultado de un esfuerzo aplicado:
Ejemplos: Cambio en longitud por unidad de
longitud; cambio en volumen por unidad de
volumen.
Esfuerzo  F
A
N
m2
Unidades : Pa 

10. Esfuerzo y deformación longitudinal
L
L
A
A
F
Para alambres, varillas y
barras, existe un esfuerzo
longitudinal F/A que
produce un cambio en
longitud por unidad de
longitud. En tales casos:
Esfuerzo  F
A
 L
L
Deformación 

11. Ejemplo 1. Un alambre de acero de 10 m
de largo y 2 mm de diámetro se une al
techo y a su extremo se une un peso de
200 N. ¿Cuál es el esfuerzo aplicado?
L
L
A
A
F
Primero encuentre el área del
alambre:
4 4
D2
 (0.002 m)2
A  
A = 3.14 x 10-6 m2
Esfuerzo
6.37 x 107 N/m2
200 N
A 3.14 x 106
m2
Esfuerzo 
F


12. Ejemplo 1 (Cont.) Un alambre de acero
de 10 m se estira 3.08 mm debido a la
carga de 200 N. ¿Cuál es la
deformación longitudinal?
L
L
Dado: L = 10 m; L = 3.08 mm
Deformación longitudinal
3.08 x 10-4
Deformación 
L

0.00308m
L 10 m

13. El límite elástico
El límite elástico es el esfuerzo máximo que un cuerpo puede
experimentar sin quedar deformado permanentemente.
W
W
2 m
Si el esfuerzo supera el límite elástico, la
longitud final será mayor que los 2 m originales.
Bien
Más allá del
límite
F
W
2 m
Esfuerzo  F
A

14. Resistencia a la rotura
La resistencia a la rotura es el esfuerzo máximo que un
cuerpo puede experimentar sin romperse.
Si el esfuerzo supera la resistencia a la
rotura, ¡la cuerda se rompe!
W
W
F
W W
W
2 m
Esfuerzo  F
A

15. Ejemplo 2. El límite elástico para el
acero es 2.48 x 108 Pa. ¿Cuál es el
peso máximo que puede soportar sin
superar el límite elástico?
L
L
A
A
F
Recuerde: A = 3.14 x 10-6 m2
F = (2.48 x 108 Pa)(3.14 x 10-6 m2) F = 779 N
A
F = (2.48 x 108 Pa) A
Esfuerzo 
F
 2.48 x 108
Pa

16. Ejemplo 2 (Cont.) La resistencia a la
rotura para el acero es 4089 x 108 Pa.
¿Cuál es el peso máximo que puede
soportar sin romper el alambre?
L
L
A
A
F
Recuerde: A = 3.14 x 10-6 m2
F = (4.89 x 108 Pa) A
F = (4.89 x 108 Pa)(3.14 x 10-6 m2) F = 1536 N
A
Esfuerzo 
F
 4.89 108
Pa

17. El módulo de elasticidad
Siempre que el límite elástico no se supere,
una deformación elástica (deformación) es
directamente proporcional a la magnitud de la
fuerza aplicada por unidad de área (esfuerzo).
esfuerzo
deformación
Módulo de elasticidad 

18. Ejemplo 3. En el ejemplo anterior, el
esfuerzo aplicado al alambre de acero fue
6.37 x 107 Pa y la deformación fue 3.08 x 10-4.
Encuentre el módulo de elasticidad para el acero.
L
L
Módulo = 207 x 109 Pa
Este módulo de elasticidad longitudinal se llama
módulo de Young y se denota con el símbolo Y.
esfuerzo 6.37 107
Pa
Módulo  
deformación 3.08  104

19. Módulo de Young
Para materiales cuya longitud es mucho mayor que el
ancho o espesor, se tiene preocupación por el módulo
longitudinal de elasticidad, o módulo de Young (Y).
L /L
Y 
F / A

FL
AL
esfuerzo longitudinal
deformaciónlongitudinal
Módulo deYoung 
Unidades: Pa

20. Ejemplo 4: El módulo de
Young para el latón es 8.96 x
1011 Pa. Un peso de 120 N se
une a un alambre de latón de 8 8 m
L
120 N
m de largo; encuentre el
aumento en longitud. El
diámetro es 1.5 mm.
Primero encuentre el área del alambre:
4 4
D2
 (0.0015 m)2
A   A = 1.77 x 10-6 m2
Y  or L 
FL
AY
FL
AL

21. Ejemplo 4: (continuación)
8 m
L
120 N
Y = 8.96 x 1011 Pa; F = 120 N;
L = 8 m; A = 1.77 x 10-6 m2
F = 120 N; L = ?
FL
AY
Y  or L 
FL
AL
(120 N)(8.00 m)
AY (1.77 x 10-6
m2
)(8.96 x1011
Pa)
L 
FL

L = 0.605 mm
Aumento en longitud:

22. Esfuerzo por tracción y compresión:
Consideremos un cuerpo al que se le aplican dos fuerzas
exteriores iguales paralelas en sentido contrario y
perpendiculares a dos secciones
Si F>0 (hacia fuera del cuerpo)
Si F<0 (hacia dentro del cuerpo)
fuerza de
tracción
fuerza de
compresión
F F F F

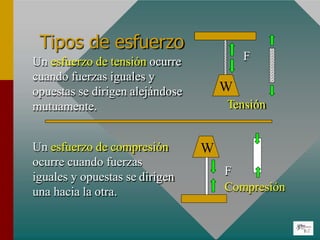
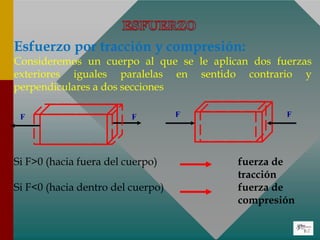
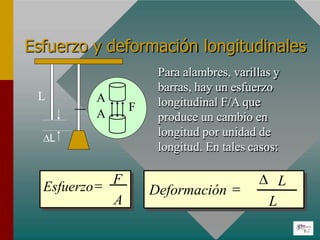
23. Se define el esfuerzo tensor y compresor “ ”
como el cociente entre la fuerza (de tensión o
compresión) aplicada perpendicularmente al
área de la sección transversal sobre la que se
aplica y dicha área.
El resultado será un cambio en la longitud el mismo.
Si Lo es la longitud original del cuerpo y L su longitud
después de aplicar el esfuerzo, el alargamiento o
elongación producido será ΔL = L - Lo
A
 
F [N/m2 =Pa]
si ΔL>0
si ΔL<0
L>Lo
L<Lo
fuerza de tracción
fuerza de compresión

24.  
L
LO

Y 
 [N/m2 =Pa]
[adimensional]
La deformación producida dependerá de la tensión o
compresión por unidad de área transversal sobre la que
se aplica la fuerza (esfuerzo tensor o compresor).
Si el esfuerzo aplicado sobre el cuerpo no es demasiado
grande (reversible), experimentalmente se encuentra
que el esfuerzo aplicado es directamente proporcional a
la deformación produci
Deformación longitudinal ():
Es el cociente entre la variación de longitud
producida y la longitud inicial del cuerpo.

25. a= límite de proporcionalidad
(desde O – a) Ley de
Hooke:
ε = Y
b=límite
(desde
de elasticidad
O – b) zona
elástica
a partir de b hasta d
zona inelástica o plástica
d=punto de ruptura o de
fractura o límite de
ruptura Deformación
Esfuerzo
a
Límite deproporcionalidad
b
Límite de elasticidad o punto cedente
d
Punto de
fractura
o ruptura
c
Comportamiento
plástico
Comportamiento elástico
< 1% 30%
Deformación permanente
O

26. Un esfuerzo de tensión ocurre
cuando fuerzas iguales y
opuestas se dirigen alejándose
mutuamente.
Un esfuerzo de compresión
ocurre cuando fuerzas iguales
y opuestas se dirigen una
hacia la otra.
F
W
Tensión
F
W
Compresión
Resumen
Tipos de esfuerzo

27. Esfuerzo y deformación longitudinales
L
L
A
A
F
Para alambres, varillas y
barras, hay un esfuerzo
longitudinal F/A que
produce un cambio en
longitud por unidad de
longitud. En tales casos:
Esfuerzo F
A
L
L

Deformación 

28. El límite elástico
El límite elástico es el esfuerzo máximo que un
cuerpo puede experimentar sin quedar
permanentemente deformado.
La resistencia a la rotura
La resistencia a la rotura es el mayor estrés que
un cuerpo puede experimentar sin romperse.

29. Módulo de Young
Para materiales cuya longitud es mucho mayor que el
ancho o el espesor, se tiene preocupación por el
módulo longitudinal de elasticidad, o módulo de
Young Y.
L /L
Y 
F / A

FL
AL
esfuerzo longitudinal
deformaciónlongitudinal
Módulo deYoung 
N
m2
Unidades  Pa 