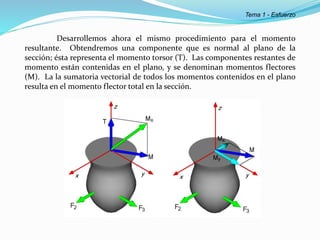
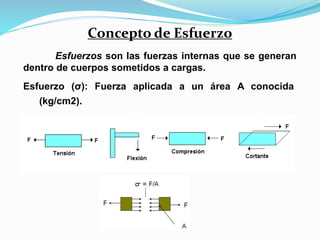
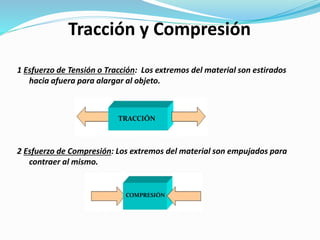
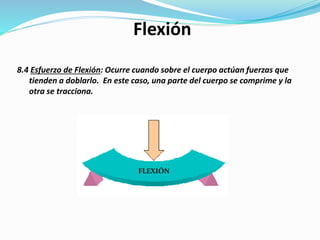
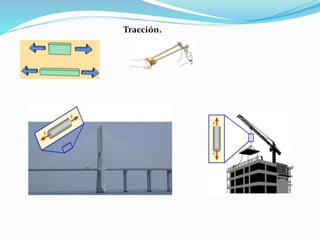
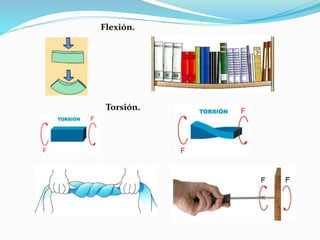
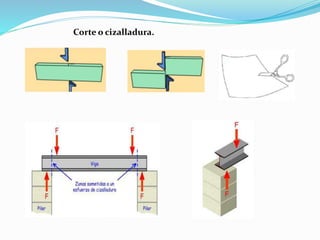
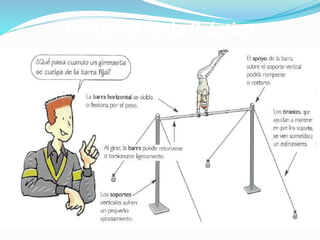
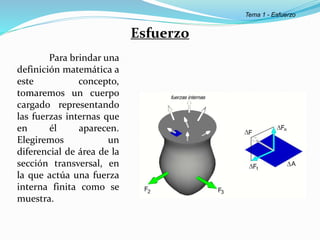
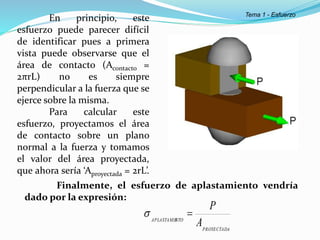
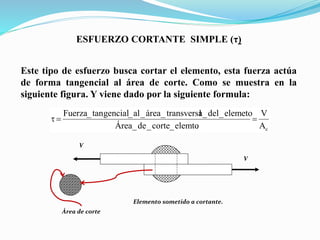
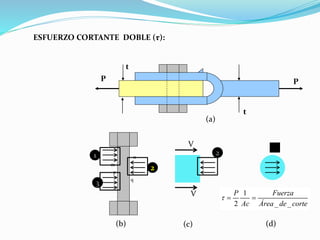
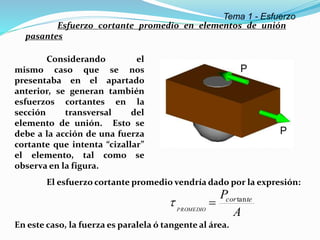
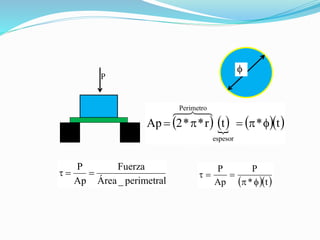
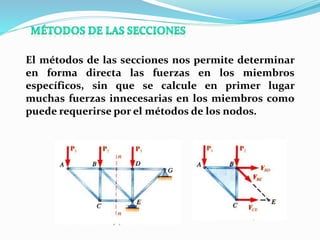
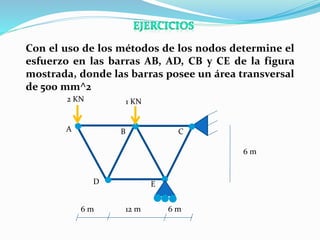
El documento describe la asignatura de Resistencia de Materiales en la Universidad Nacional Experimental Francisco de Miranda, enfocándose en la mecánica de estructuras y los esfuerzos internos generados bajo cargas externas. Se analizan definiciones, tipos de esfuerzos, así como condiciones de equilibrio y métodos de diseño de estructuras para garantizar su resistencia. Se incluyen conceptos fundamentales como el esfuerzo normal, cortante, y de aplastamiento, además de técnicas de análisis como los métodos de nodos y secciones.