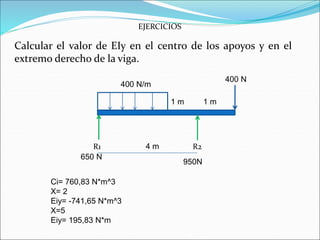
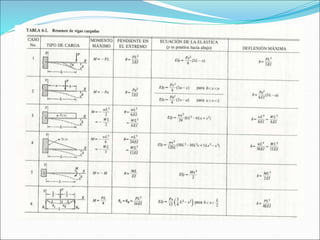
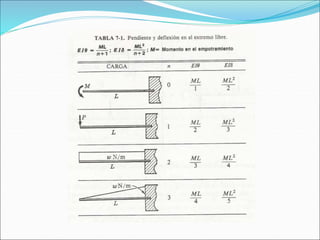
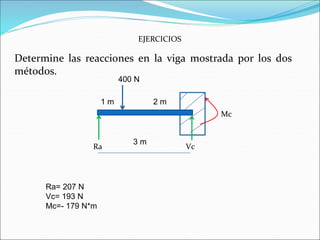
El documento presenta los objetivos y métodos para determinar la ecuación de la elástica en vigas isostáticas e hiperestáticas. Los objetivos incluyen determinar la deflexión en cualquier punto de la elástica usando el método de doble integración o superposición considerando diferentes cargas y condiciones de apoyo. Los métodos principales son la doble integración, que produce ecuaciones para la pendiente y deflexión, y la superposición, que determina la deflexión como suma de las deflexiones parciales de cada carga.