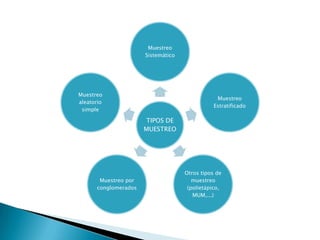
Este documento presenta diferentes tipos de muestreo para obtener información de una muestra representativa de una población, incluyendo muestreo probabilístico como muestreo aleatorio simple y muestreo estratificado, y muestreo no probabilístico como muestreo sistemático. Además, explica cómo determinar el tamaño de la muestra para estudios cuantitativos y cualitativos utilizando fórmulas estadísticas.

1. MODULO DE ESTADISTICA
VERONICA FERNANDEZ
MAESTRIA EDUCACIÓN INICIAL
2013

2. • Trata de obtener la información de una pequeña porción (muestra) de la población que
debe representar a la totalidad
• Para tomar una muestra de la población contamos con diferentes técnicas de muestreo.
• Podemos aplicar muestreo no probabilístico y muestreo probabilístico.
• Aunque el muestreo no probabilístico suele aplicarse en la vida corriente, debe aplicarse a
investigaciones en las que estamos seguros de la homogeneidad de la población o en
investigaciones en las cuales el equivocarse no traiga consecuencias graves
• Este tipo de muestreo no nos permite predecir el tipo de distribución de los resultados
producidos ni estimar cuanto difieren estos resultados del verdadero valor que se busca.

3. Muestreo
Sistemático
Muestreo
aleatorio
simple
Muestreo
Estratificado
TIPOS DE
MUESTREO
Muestreo por
conglomerados
Otros tipos de
muestreo
(polietápico,
MUM,...)

4. MUESTREO ALEATORIO SIMPLE (M.A.S.)
Llamado también muestreo irrestrictamente aleatorio, consiste en
la selección de n elementos entre los N que constituyen la
población, de modo que todas las muestras posibles de tamaño n
tengan la misma probabilidad de ser obtenidas.
-
- Se eligen individuos de la población de estudio, de manera que
todos tienen la misma probabilidad de aparecer, hasta alcanzar el
tamaño muestral deseado.
- Se puede realizar partiendo de listas de individuos de la
población, y eligiendo individuos aleatoriamente con un
ordenador.
- Normalmente tiene un coste bastante alto su aplicación.

5. MUESTREO SISTEMÁTICO
- Partimos de una población de tamaño N , y agrupamos sus elementos en n zonas de
tamaño k (N=n k).
- Este tipo de muestreo suele ser de fácil y rápida aplicación y además podemos tener
ventajas, con relación al muestreo aleatorio simple o aleatorio estratificado. Lo cual
depende mucho de las propiedades de la población.
- Se tiene una lista de los individuos de la población de estudio. Si queremos una muestra
de un tamaño dado, elegimos individuos igualmente espaciados de la lista, donde el
primero ha sido elegido al azar.
- CUIDADO: Si en la lista existen periodicidades, obtendremos una muestra sesgada.

6. MUESTREO ESTRATIFICADO
- En el muestreo estratificado, la población se divide primero en sub poblaciones.
- Las sub poblaciones se denominan estratos.
- Dentro de cada estrato se selecciona una muestra separada a partir de todas las
unidades que componen ese estrato, las extracciones deben hacerse independientemente en
los diferentes estratos.
- Además de procurar mediante la estratificación muestras más representativas, puede
lograrse un mejor aprovechamiento de la organización administrativa y en general de las
particularidades de diferentes grupos de elementos de la población.
- Al extrapolar los resultados a la población hay que tener en cuenta el tamaño relativo
del estrato con respecto al total de la población

7. MUESTREO POR GRUPOS O
CONGLOMERADOS
Se aplica cuando es difícil tener una lista de todos los individuos que forman parte de la población de
estudio, sabemos que se encuentran agrupados naturalmente en grupos.
Se realiza eligiendo varios de esos grupos al azar y elegidos algunos podemos estudiar a todos los
individuos de los grupos elegidos o bien seguir aplicando dentro de ellos más muestreos por
grupos, por estratos.
Al igual que en el muestreo estratificado, al extrapolar los resultados a la población hay que tener en
cuenta el tamaño relativo de unos grupos con respecto a otros
Las ventajas:
- No se necesita un marco muy específico, utiliza como marco divisiones territoriales , áreas
geográficas.
- El costo por elemento es menor.
Las desventajas:
- La varianza por elemento es mayor, lo que resulta de la homogeneidad de los elementos en los
conglomerados.
- La eficiencia de este tipo de muestreo disminuye al aumentar el tamaño de los
conglomerados, cuando en realidad este tipo de muestreo es más útil en caso de poblaciones muy
numerosas en las que se puedan construir conglomerados grandes.

8. Determinación del Tamaño de la Muestra
Cuando el estudio es de carácter cualitativo
a. Cuando el estudio es de carácter
cualitativo
b. Cuando al población es finita (se
conoce N) o el muestreo es sin
reposición
2
NZ PQ
n
2
( N  1) E 2  Z PQ

9. P=
Proporción de la poblaciónón que posee la
característica de estudio; que se conoce por estudios
anteriores o similares.
Q=
(1-P) Proporción dela población que no posee la
característica de estudio.
Z=
Valor que se obtiene de la distribución normal, para
que un nivel de significación de . Generalmente se
toma
Z=
1.96 para un nivel de significancia del 95%
Z=
2
Z=
2.575 para un nivel del 99%
E=
Error de estimación. Valor que lo determina el
investigador. Se sugiere valores en torno al 5%.
N=
Número de los elementos del universo o de la
población
para un nivel de significancia del 95,5%

10. Determinación del Tamaño de la Muestra
Cuando el estudio es de carácter
cuantitativo
a. Cuando no se conoce el
tamaño N de la población
o éste es infinito.
2
Z  2
n 2
E
b. Cuando al población es
finita (se conoce N) o el
muestreo es sin
reposición:
NZ 
n
2 2
( N  1) E  Z
2

2
2
Donde:
 =
es la desviación estándar que se conoce por
antecedentes anteriores.
Si no se conoce , se
obtendrá de una muestra piloto.

11. •Las hipótesis nos indican lo que estamos buscando o tratando de probar y pueden definirse como explicaciones
tentativas del fenómeno investigado, formuladas a manera de proposiciones.
DEFINICIÓN
•Las hipótesis deben referirse a una situación social real.
•Los términos (variables) de la hipótesis tienen que ser comprensibles, precisos y lo más concreto posible.
•La relación entre variables propuesta por una hipótesis debe ser clara y verosímil (lógica).
•Los términos de la hipótesis y la relación planteada entre ellos, deben poder ser observados y medidos, es decir, tener
CARACTERISTICAS
referentes en la realidad.
•Las hipótesis deben estar relacionadas con técnicas disponibles para probarlas.
•Del análisis de un postulado de una teoría.
•De generalizaciones empíricas o pertinentes al problema de investigación .
•De estudios revisados o antecedentes consultadas.
DE DONDE
PROVIENE
•En planteamientos del problema cuidadosamente revisados.
•Se debe evitar “hipotetizar” algo comprobado o “hipotetizar” algo que ha sido contundentemente rechazado.

12. TIPOS DE HIPOTESIS
HIPOTESIS DE
INVESTIGACION HI
Descriptiva
Correlacionales
Diferencia entre
grupos
Relación de
causalidad
NULAS Y
ALTERNATIVAS
ESTADISTICAS
De Estimación
De Diferencia
de Medidas
De Correlación

13. HIPOTESIS
CORRELACIONALES
HIPOTESIS DESCRIPTIVA
- Involucran dos (bivariada) o más variables
(multivariada)
- Se plantean en estudios descriptivos
- Pueden involucrar una sola variable
- Señalan la relación entre dos o más variables.
-Señalan la presencia de cierto fenómeno
en la población.
Ejemplo:
El porcentaje de aceptación
autoridad N.N. es del 50%
de
la
Se comprueban usando porcentajes o
tasas de crecimiento.
Ejemplo:
Los estudiantes que tienen altas calificaciones en
Matemáticas, tienden a tener altas calificaciones
en Estadística.
- No se determina variable dependiente e
independiente.
- Se prueba mediante Chi cuadrado
correlación con Pearson o Spearman.
y la

14. HIPOTESIS DE LA DIFERENCIA ENTRE
GRUPOS
HIPOTESIS DE RELACIÓN DE
CAUSALIDAD
- Se utiliza para comparar grupos.
En
estudios
experimentales.
experimentales
o
cuasi
-
Establecen relación causa – efecto.
Ejemplo:
Ejemplo:
El rendimiento académico de los (as) estudiantes
del paralelo A es superior respecto al
rendimiento de los (as) estudiantes del paralelo B
utilizando métodos diferentes.
El divorcio de los padres causa bajo
rendimiento en los hijos(as)
Se prueba mediante puntaje z normalizado o
t-student.
Se prueba mediante Chi cuadrado y la
correlación con Pearson o Spearman

15. HIPOTESIS NULAS Ho
- Son, en un sentido, el reverso de las hipótesis de
investigación.
HIPOTESIS ALTERNATIVA
Ha
- Son posibilidades 'alternativas " ante las
hipótesis de investigación y nula. Ofrecen otra
- Sirven para refutar o negar lo que afirma la hipótesis de
investigación.
- Descripción o explicación distintas a las que
proporcionan estos tipos de hipótesis.
Ejemplo, si la hipótesis de investigación propone: "Los
adolescentes le atribuyen más importancia al atractivo físico
en sus relaciones heterosexuales que las mujeres", la nula
postularía:
Por ejemplo, si la hipótesis de investigación
establece: "Esta silla es roja", la nula afirmará:
"Esta silla no es roja", y podrían formularse una o
"Los jóvenes no le atribuyen más importancia al atractivo
físico en sus relaciones heterosexuales que las adolescentes".
más hipótesis alternativas: "Esta silla es azul",
"Esta silla es verde", "Esta silla es amarilla",

16. HIPOTESIS DE ESTADISTICA
DE ESTIMACIÓN
- l promedio mensual de casos de transtorno psiconeurótico
caracterizados por reacción asténica, atendidos en los
hospitales de la Ciudad de Linderbuck es mayor a 200".
- Primero: analizar cuál es la estadística a que su hipótesis
hace referencia (en el ejemplo se trata de un promedio
mensual de casos atendidos).
- Segundo: encontrar cómo se simboliza esa estadística
(promedio se simboliza como X).
- Tercero:
estadística:
traducir
la
hipótesis
de
investigación
en
Hi: X > 200 (promedio mensual de casos atendidos)
Ho: X = 200 (“el promedio mensual de casos... es igual a
200”)
Ha: X < 200 (“el promedio mensual de casos ... es menor
que 200”)
HIPOTESIS DE ESTADISTICA
DE CORRELACIÓN
- “A mayor cohesión en un grupo, mayor
eficacia en el logro de sus metas primarias“
- Hi: r x y  0 (no es igual a cero, o lo que es lo
mismo ambas variables están correlacionadas)
- Hr xy = 0 (“las dos variables no están
correlacionadas; su correlación es cero”).
Otro ejemplo:
- Hi: R xyz  0 («la correlación entre las
variables autonomía, variedad y motivación
intrínseca no es igual a cero").
- Ho: R xyz = 0 ("no hay correlación").

17. HIPOTESIS DE LA DIFERENCIA DE MEDIDAS
- Existe una diferencia entre el promedio de
editoriales mensuales que dedicó, durante el
último año, al tema del desarme mundial el
diario 'Telex', y el que dedicó el diario
'Noticias'.
- La estadística que se compara entre los
grupos (editoriales de "Telex" , un grupo, y
editoriales de "Noticias", otro grupo) es el
promedio (X). La hipótesis estadística se
formularía así:
- Hi: X1  X2
- Ho: X1 = X2 ("No hay diferencia entre los
promedios de los dos grupos“)

18. 1) Enunciado de
la hipótesis nula
y alternativa
2) Elección del
nivel de
6) Exposición de
las conclusiones.
significación (∝)
3) Selección del
estadístico de
prueba.
5) Cálculo del
estadístico.
4) Determinación
de la región
crítica.