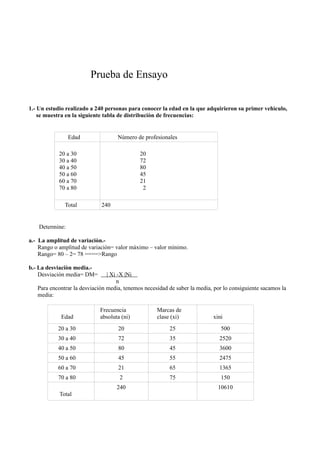
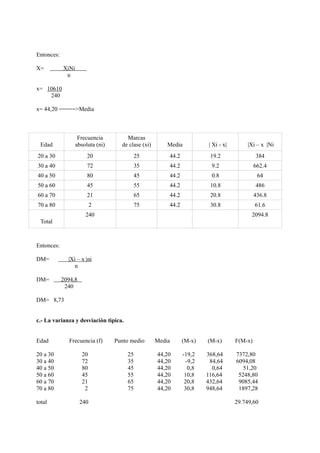
Este documento presenta varios problemas de probabilidad y estadística. Calcula probabilidades asociadas con extraer cartas de una baraja, que clientes de un banco tengan diferentes tipos de cuentas, y la precisión de bombarderos. También analiza una distribución normal para determinar probabilidades dentro y fuera de ciertos rangos.

1. Prueba de Ensayo
1.- Un estudio realizado a 240 personas para conocer la edad en la que adquirieron su primer vehìculo,
se muestra en la siguiente tabla de distribuciòn de frecuencias:
Edad Nùmero de profesionales
20 a 30 20
30 a 40 72
40 a 50 80
50 a 60 45
60 a 70 21
70 a 80 2
Total 240
Determine:
a.- La amplitud de variaciòn.-
Rango o amplitud de variaciòn= valor màximo – valor mìnimo.
Rango= 80 – 2= 78 ====>Rango
b.- La desviaciòn media.-
Desviaciòn media= DM= | Xi -X |Ni
n
Para encontrar la desviaciòn media, tenemos necesidad de saber la media, por lo consiguiente sacamos la
media:
Frecuencia Marcas de
Edad absoluta (ni) clase (xi) xini
20 a 30 20 25 500
30 a 40 72 35 2520
40 a 50 80 45 3600
50 a 60 45 55 2475
60 a 70 21 65 1365
70 a 80 2 75 150
240 10610
Total

2. Entonces:
X= XiNi
n
x= 10610
240
x= 44,20 =====>Media
Frecuencia Marcas
Edad absoluta (ni) de clase (xi) Media | Xi - x| |Xi – x |Ni
20 a 30 20 25 44.2 19.2 384
30 a 40 72 35 44.2 9.2 662.4
40 a 50 80 45 44.2 0.8 64
50 a 60 45 55 44.2 10.8 486
60 a 70 21 65 44.2 20.8 436.8
70 a 80 2 75 44.2 30.8 61.6
240 2094.8
Total
Entonces:
DM= |Xi – x |ni
n
DM= 2094,8
240
DM= 8,73
c.- La varianza y desviaciòn tìpica.
Edad Frecuencia (f) Punto medio Media (M-x) (M-x) F(M-x)
20 a 30 20 25 44,20 -19,2 368,64 7372,80
30 a 40 72 35 44,20 -9,2 84,64 6094,08
40 a 50 80 45 44,20 0,8 0,64 51,20
50 a 60 45 55 44,20 10,8 116,64 5248,80
60 a 70 21 65 44,20 20,8 432,64 9085,44
70 a 80 2 75 44,20 30,8 948,64 1897,28
total 240 29.749,60

3. S= f(M-x) =
n-1
S= 29.749,60
240-1
S= 124,475
S= 11,16 Desviaciòn Tìpica de datos agrupados
d.- El coeficiente de variaciòn.
Cv= 11,16 = 100
44,2
cv= 25,24%
e.- El coeficiente de asimetrìa de Pearson.
Para este coeficiente, debemos saber el valor de la media (44;20); y el valor de la mediana (que la debe-
mos obtener con un ejercicio); y el valor de la desviaciòn tìpica o estàndar (11,16).
Entonces obtengamos la mediana:
Edad Nùmero de profesionales Frecuencia acumulada
(n) (FA)
20 a 30 20 20
30 a 40 72 92
40 a 50 80 172
50 a 60 45 217
60 a 70 21 238
70 a 80 2 240
Total 240
Utlizamos la fòrmula PosMe= n+1
2
PosMe = 240+1
2
PosMe = 241
2
Posme = 120,5

4. Utlizamos la fòrmula de la mediana:
Me = Li 2 - FA
ni
Me = 40 120,5 – 92
80
Me = 40 + 3,56
Me = 43,56 Mediana
Fòrmula del coeficiente de Pearson SK = 3 (x – mediana)
s
Sk = 3 (44,2 – 43,56)
11,16
Sk = 3 (0,64)
11,16
Sk = 1,92
11,16
Sk = 0,17
Por lo consiguiente este valor 0,17 nos indica que tanto la media como la mediana son pràcticamente
iguales, que la distribuciòn es simètrica y que no se presenta ningùn sesgo.
f.- El Cuartil 2.
Q2= Mediana; hay que decir que el cuartil 2 es la mediana.
Q2= Mediana= 43,56. Hacièndolo directamente, pero haciendo por el procedimiento que enseña el li-
bro es:
Ordenemos los datos:
2
20
21
45
72
80
La fòrmula es L50= (n+1) P ò Q2=(n+1) Q
100 4
L50=(6+1) 50 ò Q2=(6+1) 2
100 4
L50= 3,5 ò Q2= 3,5
El valor L50=3,5 ò Q2= 3,5. Nos indica que nuestro valor està entre la tercera y la cuarta posiciòn,

5. pero todavìa no sabemos el valor exacto, para obtenerlo hacemos lo siguiente:
0,5 (24) = 12, èsto quiere decir que al tercer valor (21) le debemos sumar 12, entonces:
21 + 12 = 33 èste valor es el cuartil 2.
Vemos que este valor 33, es un dato totalmente diferente a la mediana = 43,56 (dato obtenido con las
frecuencias acumuladas), pero confirmo que el dato obtenido con el procedimiento de los cuartiles
del libro es 33.
g.- El decil 5.
Se podrìa utilizar la fòrmula D5 = (n+1) D
10
Decimos tambièn; que el decil 5, no es otra cosa que la mediana o lo mismo que el cuartil 2, y para no
estar repitiendo el procedimiento antes hecho, me limito a escribir que el decil 5 es 33.
h.- El percentil 50.
Se podrìa utilizar la fòrmula L50 = (n+1) P
100
Repito y confirmo que es 33.
2.- En una baraja que contiene 52 cartas:
a.- ¿Cuàl es la probabilidad que la primera carta que se saque sea una de espadas?
La probabilidad es 0,25 que se obtiene de la siguiente manera:
13 = 0,25
52
b.- ¿Cuàl es la probabilidad de que la primera carta seleccionada sea un as de corazones?
La probabilidad es 0,019 que se obtiene de la siguiente manera:
1 = 0,019
52
c.- Si se extrae una carta y se deja a un lado, ¿Cuàl es la probabilidad de que al extraer una segunda
sea un dos de espadas?
La probabilidad es 0,0196 porque al extraer una carta, el mazo queda con 51 cartas y se obtiene asi:
1 = 0,0196
51

6. d.- Si se extrae una carta y se la devuelve, ¿Cuàl es la probabilidad de que al extraer una segunda
sea un dos de espadas?
La probabilidad es 0,019; porque el acto de extraer y despuès devolver la carta no me cambia nada,
quiere decir que en el mazo de cartas estàn todavìa las 52; se lo obtiene de la siguiente manera:
1 = 0,019
52
3.- Un banco local reporta que 80% de sus clientes tiene una cuenta de cheques, 60% una cuenta de
ahorros, y 50% tiene ambas. Si selecciona un cliente al azar, ¿Cuàl es la probabilidad de que èste
tenga una cuenta de cheques o una cuenta de ahorros? ¿cuàl es la probabilidad de que el cliente
no tenga ninguna de las dos?
80% cuenta cheques
60% cuenta ahorros
50% ambas
80% 0,8
60% 0,6
50% 0,5
P(AoB) = P(A) + P(B) – P(AyB)
(0,8 + 0,6) – 0,5
1,4 – 0,5 = 0,9 Probabilidad de que el cliente tenga una cuenta de cheques o una de ahorros.
Entonces decimos que hay 0,9 ò 90% de probabilidades de que “el cliente tenga una cuenta de che-
ques o una de ahorros”.
Despuès usamos la siguiente fòrmula para encontrar al cliente que “no tenga ninguna de las dos”.
1- P ò lo que es:
1 – 0,9 = 0,1 Probabilidad de que el cliente no tenga ninguna de las dos.
Entonces llegamos a la conclusiòn de que hay 0,1 ò 10% de probabilidades de que “el cliente no tenga
ninguna de las dos”.
4.- La probabilidad de que un aviòn bombardero acierte en su objetivo en una misiòn es 0,80%.
Se envìan 4 bombarderos hacia el mismo objetivo, ¿cuàl es la probabilidad de que:
a.- todos den en el blanco?
Para resolver esta interrogante utilizaremos la regla especial de la multiplicaciòn:
P(A y B y C y D) = P(A) P(B) P(C) P(D)
“acierte a su objetivo” es 0,80% entonces:

7. (0,80) (0,80) (0,80) (0,80) = 0,4096 Probabilidad que todos den en el blanco.
b.- ninguno acierte el objetivo?
Utilizamos la regla especial de la multiplicaciòn:
P(A y B y C y D) = P(A) P(B) P(C) P(D)
“que no acierte a su objetivo” es 0,20 entonces:
(0,20) (0,20) (0,20) (0,20) = 0,0016 Probabilidad que ninguno acierte el objetivo.
c.- ¿al menos uno acierte en el blanco?.
Aplicamos la regla del complemento:
1 – 0,0016 = 0,9984
5.- Una poblaciòn normal tiene media 50 y deviaciòn estàndar 4.
a.- Calcule la probabilidad de tener un valor entre 44 y 55.
u = 50
=4
44- 50 = -6 = -1,5 =====> 0,4232
4 4
+ 0,8276
55 – 50 = 5 = 1,25 =====> 0,3944
4 4
b.- Evalùe la probabilidad de tener un valor mayor que 55.
0,50 – 0,3944 = 0,1056
c.- Determine la probabilidad de tener un valor entre 52 y 55.
52 – 50 = 2 = 0,5 ====> 0,1915
4 4
- 0,2029
55 – 50 = 5 = 1,25 ====> 0,3944
4 4