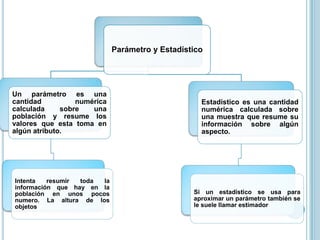
El documento define conceptos estadísticos básicos como estadística, población, muestra, parámetro, estadístico, variables, escalas de medición y tipos de muestreo. Explica que la estadística estudia características de poblaciones mediante la recolección y análisis de datos. Define población como el conjunto total y muestra como un subconjunto seleccionado. Distingue parámetros que resumen poblaciones de estadísticos que resumen muestras. También describe escalas ordinal, de intervalo

1. Republica Bolivariana de Venezuela
Ministerio de Educación Superior
Instituto Universitario “Antonio José de Sucre”
Extensión - Lara
Alumno:
Daniel Mogollón
C.I: 23.854.876
Prof: Oscar Pereira

2. Definición de estadística:
La Estadística es la parte de las Matemáticas que se encarga del
estudio de una determinada característica en una población, recogiendo
los datos, organizándolos en tablas, representándolos gráficamente y
analizándolos para sacar conclusiones de dicha población.
Ejemplo: Se quiere conocer el estado sanitario de un país, a través de
ciertos parámetros como la tasa de morbilidad o mortalidad de la
población.
Según se haga el estudio sobre todos los elementos de la
población o sobre un grupo de ella, vamos a diferenciar dos tipos de
Estadística:
Estadística descriptiva. Realiza el estudio sobre la población completa,
observando una característica de la misma y calculando unos parámetros
que den información global de toda la población.
Ejemplo: La cantidad de robos ocurridos el último mes en una ciudad
concreta.

3. Estadística inferencial: Realiza el estudio descriptivo sobre un
subconjunto de la población llamado muestra y, posteriormente,
extiende los resultados obtenidos a toda la población.
Ejemplo: De acuerdo con una encuesta desarrollada por una empresa
sobre telefonía residencial en el 2013, el gasto mensual promedio por
cliente es 200 bolivares por cliente.
Definición de Universo, población y muestra:
Universo: En estadística es el nombre especifico que recibe
particularmente en la investigación social la operación dentro de la
delimitación del campo de investigación que tienen por objeto la
determinación del conjunto de unidades de observaciones del conjunto
de unidades de observación que van a ser investigadas.
Población: Es el conjunto formado por todos los elementos a los que
les vamos a hacer el estudio.

4. Muestra: el subconjunto de la población que elegimos para hacer un
estudio más reducido.
Ejemplo:
Se desea saber cuantos alumnos de la escuela 70 del Antonio José de
Sucre, estan realizando su servicio comunitario...
UNIVERSO: Escuela 70
POBLACION: 15 Semestres
MUESTRA: Alumnos realizando servicio

5. Parámetro y Estadístico
Un parámetro es una
cantidad numérica
calculada sobre una
población y resume los
valores que esta toma en
algún atributo.
Intenta resumir toda la
información que hay en la
población en unos pocos
numero. La altura de los
objetos
Estadístico es una cantidad
numérica calculada sobre
una muestra que resume su
información sobre algún
aspecto.
Si un estadístico se usa para
aproximar un parámetro también se
le suele llamar estimador

6. Interpretación:
Una variable estadística es cada una de las
características o cualidades que poseen los individuos de una
población que se desea estudiar.
Existen varios tipo de variables estadísticas los cuales
son:
variable cualitativa estas no se expresa mediante un número
ejemplo: la opinión de los españoles sobre el terrorismo.
variable cuantitativa se expresa mediante un número. Esta a su
vez se divide en dos tipos los cuales son variable Cuantitativa
Discreta la cual solo admite valores aislados y la variable
Cuantitativa Continua esta puede admitir cualquier valor dentro
de un intervalo.

7. Pasos para un estudio estadístico:
1. Plantear hipótesis sobre una población.
2. Decidir qué datos recoger
3. Qué individuos pertenecerán al estudio (muestras).
4. Criterios de exclusión ¿Cómo se eligen? ¿Descartamos los que
padecen enfermedades crónicas?
5. Qué datos recoger de los mismos (variables).
6. Recoger los datos (muestreo)
7. Describir (resumir) los datos obtenidos
8. Realizar una inferencia sobre la población.
9. Interpretación y Decisión.

8. Tipo de Muestreos:
Muestreo probabilístico:
Consiste en elegir una muestra de una población al azar. Podemos
distinguir varios tipos de muestreo:
Muestreo aleatorio simple
Para obtener una muestra, se numeran los elementos de la población y
se seleccionan al azar los n elementos que contiene la muestra.
Ejemplo:
Si metemos en una bolsa los nombres de las personas y los
seleccionamos sacando papelitos.

9. Muestreo aleatorio sistemático
Se elige un individuo al azar y a partir de él, a intervalos constantes, se
eligen los demás hasta completar la muestra.
Ejemplo:
si tenemos una población formada por 100 elementos y queremos
extraer una muestra de 25 elementos, en primer lugar debemos
establecer el intervalo de selección que será igual a 100/25 = 4. A
continuación elegimos el elemento de arranque, tomando
aleatoriamente un número entre el 1 y el 4, y a partir de él obtenemos
los restantes elementos de la muestra.
2, 6, 10, 14,..., 98

10. Muestreo aleatorio estratificado
Se divide la población en clases o estratos y se escoge,
aleatoriamente, un número de individuos de cada estrato proporcional
al número de componentes de cada estrato.
Ejemplo:
En una fábrica que consta de 600 trabajadores queremos tomar una
muestra de 20. Sabemos que hay 200 trabajadores en la sección A,
150 en la B, 150 en la C y 100 en la D.

11. Resumen:
Es la técnica para la selección de una muestra a partir de
una población.
Al elegir una muestra se espera conseguir que sus
propiedades sean extrapolables a la población. Este proceso
permite ahorrar recursos, y a la vez obtener resultados parecidos
a los que se alcanzarían si se realizase un estudio de toda la
población.

12. Escala Ordinal:
Llamada también escala de orden jerárquico, con ella se
establecen posiciones relativas de los objetos o fenómenos en
estudio, respecto a alguna característica de interés, sin que se
reflejen distancias entre ellos. Puede suceder que los objetos de
una categoría de las escala no sean precisamente diferentes a los
objetos de otra categoría de la escala, sino que están
relacionados entre si. Los numerales empleados en las escalas
ordinales no son cuantitativos, sino que indican exclusivamente
la posición en la serie ordenada y no "cual es" la diferencia entre
posiciones sucesivas de la escala.
Ejemplo:
A los cliente de un almacén se les hace unas preguntas para
valorar la calidad del servicio. Los clientes valoran la calidad de acuerdo a
las siguientes respuestas: 1 (excelente), 2 (bueno), 3 (regular), 3 (malo) 4
(pésimo). Estos datos son ordinales. Una valoración de 1 no indica que el
servicio es dos veces mejor que cuando se da una valoración de 2. Se
puede decir que la valoración de 1 es preferiblemente mejor que 2, y así
en los demás casos.

13. Escala de Intervalo:
Representa un nivel de medición más preciso, matemáticamente
hablando, que las anteriores; no solo se establece un orden en las
posiciones relativas de los objetos o individuos, sino que se mide
también la distancia entre los intervalos o las diferentes categorías o
clases.
Ejemplo: se está interesado en la temperatura del fundido de acero. Se
toman cuatro lecturas cada dos horas: , , , y F. Obviamente los datos
pueden ser ordenados (semejante a los datos ordinales) en orden
ascendente de temperatura indicando temperatura más fria, menos fria,
y asi sucesivamente. Además , las diferencias entre los valores
ordenados pueden ser comparadas. Aquí el intervalo entre los valores
de los datos y representan un incremento en la temperatura deF, y asi
los demás intervalos

14. Escala de Razón:
Cuando una escala tiene todas las características de una escala de
intervalo y además un punto cero real en su origen, se llama escala
de razón. Además de distinción, orden y distancia, ésta es una escala
que permite establecer en que proporción es mayor una categoría de
una escala que otra. El cero absoluto o natural representa la nulidad
de lo que se estudia.
Ejemplo:
el peso de cuatro piezas fundidas de metal son 2.0, 2.1, 2.3 y 2.5 kg.
El orden(ordinal) y la diferencia (intervalo) en los pesos puede ser
comparado. Así, el incremento de peso de 2.0 a 2.1 es de 0.1 kg, el
cual es el mismo que el que existe entre 2.3 y 2.4 kg. También,
cuando comparamos los pesos de 2.0 a 2.4 kg, se encuentra una
razón significativa: el peso de una pieza de metal de 2.4 kg es un 20%
más pesada que una que pese 2.0 kg. Existe un cero natural o real
para la escala, así 0kg implica no peso.