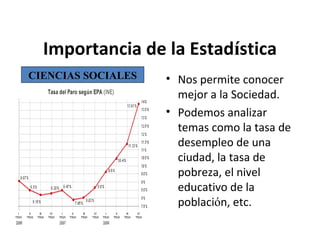
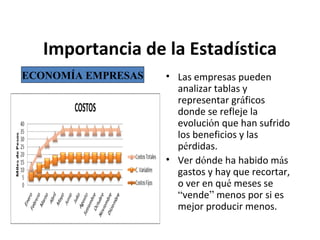
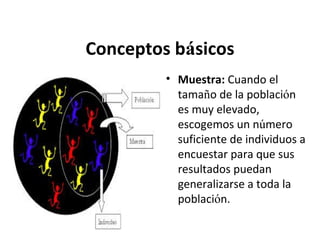
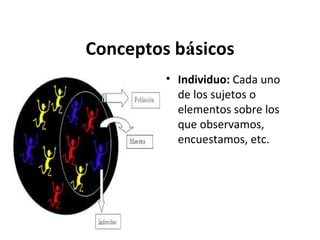
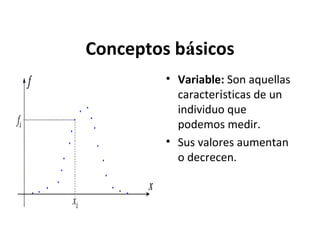
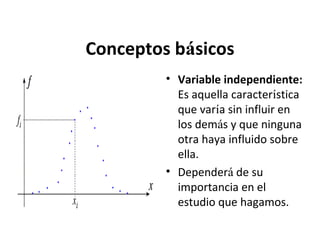
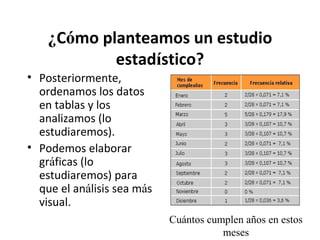
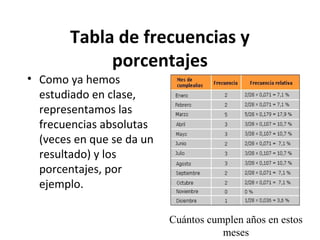
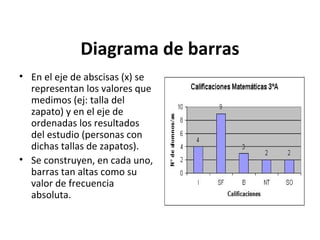
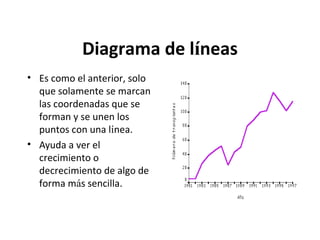
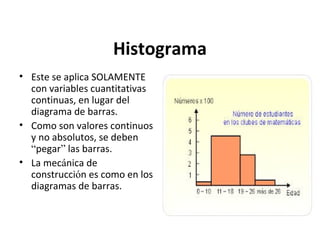
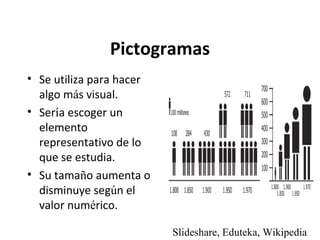
Este documento explica los conceptos básicos de la estadística. La estadística se encarga de describir, analizar e interpretar conjuntos de datos para comprender mejor las características de una población. Incluye definiciones de términos como población, muestra, variable e instrumentos para recoger datos como encuestas y entrevistas. También explica cómo planificar un estudio estadístico y diferentes técnicas de muestreo así como representar los datos mediante tablas y gráficos.

1. ¿Qué es la Estadística?
• Es la rama de las
Matemáticas que se
encarga de describir,
analizar e interpretar
las características de
un conjunto de
individuos o
población.

2. ¿Qué es la Estadística?
• Se recogen datos de
diversos tipos para
construir informes
donde se analicen
situaciones y
cuestiones
relacionadas con un
tema determinado.

3. ¿Qué es la Estadística?
• Aunque pueden
recogerse datos
numéricos
(cuantitativos) o
escritos (cualitativos),
el tratamiento que se
hace con los datos es
numérico.

4. Importancia de la Estadística
CIENCIAS SOCIALES
• Nos permite conocer
mejor a la Sociedad.
• Podemos analizar
temas como la tasa de
desempleo de una
ciudad, la tasa de
pobreza, el nivel
educativo de la
población, etc.

5. Importancia de la Estadística
CIENCIAS SOCIALES
• A partir de los datos
recogidos, se pueden
crear políticas y
proyectos sociales para
mejorar la situación o al
menos mantenerla en el
caso de que sea bueno.
Tras un estudio sobre este tema...

6. Importancia de la Estadística
ECONOMÍA EMPRESAS
• Las empresas pueden
analizar tablas y
representar gráficos
donde se refleje la
evolución que han sufrido
los beneficios y las
pérdidas.
• Ver dónde ha habido más
gastos y hay que recortar,
o ver en qué meses se
“vende” menos por si es
mejor producir menos.

7. Importancia de la Estadística
DEPORTES
• Pronosticar resultados de
partidos.
• Analizar el rendimiento de
un jugador.
• Analizar si un equipo ha
sido defensivo u ofensivo
(posesión del balón,
remates totales, faltas
cometidas, goles
marcados, etc.).

8. Ejemplos de temas a trabajar en
Estadística
• Número de divorcios que se producen en
España al año.
• Aprobados y suspendidos en Matemáticas en
la Comunidad de Madrid.
• Temáticas de las que el profesorado
considera importante formarse.
• Accidentes de tráfico ocurridos en verano.

9. Conceptos básicos
• Población: Es el
conjunto total de
sujetos sobre el que
estamos realizando el
estudio (niños, jóvenes,
adultos, etc.).
• Ejemplo: Adolescentes
de entre 12 y 16 años
del Barrio de Usera en
Madrid.

10. Conceptos básicos
• Muestra: Cuando el
tamaño de la población
es muy elevado,
escogemos un número
suficiente de individuos a
encuestar para que sus
resultados puedan
generalizarse a toda la
población.

11. Conceptos básicos
• Individuo: Cada uno
de los sujetos o
elementos sobre los
que observamos,
encuestamos, etc.

12. Conceptos básicos
• Variable: Son aquellas
características de un
individuo que
podemos medir.
• Sus valores aumentan
o decrecen.

13. Conceptos básicos
• Variable independiente:
Es aquella característica
que varía sin influir en
los demás y que ninguna
otra haya influido sobre
ella.
• Dependerá de su
importancia en el
estudio que hagamos.

14. Conceptos básicos
• Variable dependiente:
Al aumentar o
disminuir, influye en el
aumento o
disminución de otra
(ej: A mayor
motivación, mejores
notas saco).

15. Conceptos básicos
Un estudio sobre el color de
las pupilas de las personas
sería un estudio cualitativo
• Variables cualitativas: No
se puede contar, ni
cuantificar. Son aquellos
que solamente se
representan con “letras”.
• Color del pelo, acuerdo o
desacuerdo con la reforma
laboral (Sí/No)...

16. Conceptos básicos
• Variables
cuantitativas: Miden
aquellos valores
cuantitativos, que se
cuantifican y se
miden.
• Número de hijos,
goles marcados por un
equipo...

17. Conceptos básicos
• Variable cuantitativa
discreta: Miden valores
numéricos aislados,
absolutos, que no
pueden tener decimales.
• Número de hijos, goles
marcados (un gol es un
gol, no marcas 2’3
goles).
Tienes 1, 2, 3 hijos...pero nunca
2’5 (un “medio hijo” no existe,
es uno y punto).

18. Conceptos básicos
• Variable cuantitativa
continua: Es aquello
que puede partirse en
unidades pequeñas,
como la medida de
longitud (no medimos
dos metros exactos,
sino uno y algo más).

19. ¿Cómo planteamos un estudio
estadístico?
• Primero, plantearnos
qué deseamos
estudiar y a qué
población vamos a
encuestar.
• Posteriormente,
plantear los objetivos
del estudio.

20. ¿Cómo planteamos un estudio
estadístico?
• Plantear la población,
pensar si vamos a
escoger a una muestra
o encuestamos a todo
el mundo...
• Plantear los
instrumentos que
usaremos para
recoger datos.
Los cuestionarios son instrumentos muy
comunes para recoger datos.

21. ¿Cómo planteamos un estudio
estadístico?
EJEMPLOS
• Observar y anotar
todo en un diario o
registro.
• Encuestas con
cuestionarios.
• Entrevistas.
• Grabaciones
audiovisuales.

22. ¿Cómo planteamos un estudio
estadístico?
• Posteriormente,
ordenamos los datos
en tablas y los
analizamos (lo
estudiaremos).
• Podemos elaborar
gráficas (lo
estudiaremos) para
que el análisis sea más
visual.
Cuántos cumplen años en estos
meses

23. ¿Cómo planteamos un estudio
estadístico?
• Establecemos
conclusiones y
respondemos a los
objetivos que nos
marcamos
inicialmente.
• Elaboramos un
informe incluyendo
tablas y gráficos.

24. Ejemplo de Estudio
• Tres grupos de PCPI
de Informática.
• 20 estudiantes por
grupo.
• No podemos
encuestar a todos, así
que elegimos a 10 de
cada grupo para tener
el 50% al menos.

25. Ejemplo de estudio
• Es justo que cualquier
estudiante pueda ser
encuestado.
• Debemos plantear una
técnica de muestreo
para que todo el
mundo tenga derecho
a ser encuestado.

26. Ejemplo de estudio
• Podemos usar la tabla
de números
aleatorios.
• Ordenamos al
alumnado de cada
clase por orden
alfabético y le
asignamos un número
del 1 al 20.

27. Ejemplo de estudio
• Miramos la tabla, y
escogemos los diez
primeros números que
nos salgan que se
encuentren entre el 1
y el 20.
• Ej: 10, 9, 1, 20, 5, 8,
19, 3, 1, 7

28. Ejemplo de estudio
Si os fijáis, no son los mismos
números de antes...
• Estos serían los
estudiantes de un grupo
determinado que pasarían
a ser encuestados.
• Cogemos ahora otros
grupos de números de la
tabla y hacemos lo mismo
con el otro grupo de PCPI.

29. Técnicas de muestreo
• Tabla de números
aleatorios: Es un
listado de números
que se utiliza para,
atribuyéndole un valor
numérico a unos
individuos, seleccionar
al azar a los individuos
de una población.

30. Tabla de números aleatorios (versión ampliada)

31. Técnicas de muestreo
• Bombo de bolas de
bingo: Lo mismo que
antes, pero los números
están en bolas que salen
de un bombo.
• En el ejemplo anterior,
sería meter las bolas del 1
al 20 y sacar 10, y los que
hayan salido esos serán
los elegidos.

32. Técnicas de muestreo
• Ruletas: En el ejemplo
anterior, sería dividir un
círculo en 20 “rodajas”, y
girar la ruleta. Donde
termine la ruleta, ese será
uno de los elegidos.
Girarla 10 veces para
tener los 10 individuos
escogidos, y así en los tres
grupos.
Puede hacerse a mano...

33. Técnicas de muestreo
• Dados: Un dado con
veinte caras puede ser
útil. Lanzamos 10
veces el dado y
anotamos los que
salgan. Si se repite un
número, lanzamos
otra vez y ya está. Así
con los tres grupos.
Dado con 20 caras

34. Técnicas de muestreo
• Calculadora científica:
La tecla “Ran#” saca
números aleatorios.
Escogemos los dos
primeros decimales y
vemos qué número
forman.

35. Técnica de muestreo
• Por ejemplo, del 21 al
30 serían los números
del 1 al 10 (21 = 1; 22
= 2, 23 = 3, etc.). Del
31 al 40 los del 11 al
20 (31 = 11, 32 = 12,
etc.), y así
sucesivamente.

36. Tablas y gráficos
Matemáticas
Ámbito Científico-Tecnológico

37. Tabla de frecuencias y
porcentajes
• Como ya hemos
estudiado en clase,
representamos las
frecuencias absolutas
(veces en que se da un
resultado) y los
porcentajes, por
ejemplo.
Cuántos cumplen años en estos
meses

38. Diagrama de sectores
• Representamos un
círculo, y los valores
tendrán mayor “rodaja”
(más ángulos del círculo) a
cuanto mayor sea su
valor.
• Se usan cuando no son
muchos elementos los
que se comparan (ej:
votos de partidos
políticos).

39. Diagrama de barras
• En el eje de abscisas (x) se
representan los valores que
medimos (ej: talla del
zapato) y en el eje de
ordenadas los resultados
del estudio (personas con
dichas tallas de zapatos).
• Se construyen, en cada uno,
barras tan altas como su
valor de frecuencia
absoluta.

40. Diagrama de líneas
• Es como el anterior, solo
que solamente se marcan
las coordenadas que se
forman y se unen los
puntos con una línea.
• Ayuda a ver el
crecimiento o
decrecimiento de algo de
forma más sencilla.

41. Histograma
• Este se aplica SOLAMENTE
con variables cuantitativas
continuas, en lugar del
diagrama de barras.
• Como son valores continuos
y no absolutos, se deben
“pegar” las barras.
• La mecánica de
construcción es como en los
diagramas de barras.

42. Pictogramas
• Se utiliza para hacer
algo más visual.
• Sería escoger un
elemento
representativo de lo
que se estudia.
• Su tamaño aumenta o
disminuye según el
valor numérico.
Slideshare, Eduteka, Wikipedia