Este documento presenta conceptos básicos de estadística y probabilidad. Explica que la estadística se encarga de recoger, analizar e interpretar datos de una muestra representativa de una población. Detalla los pasos para realizar un proceso estadístico como la recolección y análisis de datos, y la representación gráfica de los resultados. También define términos como población, muestra, variables cualitativas y cuantitativas, y frecuencias absolutas y relativas para describir los datos estadísticos

1. COLEGIO MUNICIPAL EXPERIMENTAL
“SEBASTIAN DE BENALCAZAR”
NOMBRE: Alejandra Santillán
CURSO: 5to “A”
TRABAJO DE MATEMÁTICA

2. ESTADÍSTICA Y
PROBABILIDAD
La estadística es la ciencia que se
encarga de recoger, analizar e
interpretar datos de una muestra
representativa.

3. ESTADÍSTICA
Un gran número de datos, referidos a fenómenos
colectivos para representar de manera sencilla y
obtener de ellos una conclusión.
Para realizar un proceso estadístico se siguen los
siguientes pasos:
1. Recolección, ordenamiento y reconteo de datos.
2. Cálculo de las mediadas de dispersión y
centralización.
3. Representación gráfica

4. Términos estadísticos
En estadística empleamos la siguiente terminología:
 Población: Conjunto formado por todos los
elementos de estudio.
 Individuo: Cada uno de los elementos de los
elementos del estudio estadístico. Generalmente se
los caracteriza por una propiedad.
 Muestra: Parte de la población que se toma de base
para el análisis del conjunto que se desea estudiar.
 Tamaño de la muestra: Es el número de elementos
de una muestra.

5. Variable cualitativa
 Los valores que toma esta variable no son
números, por ejemplo: estado civil, color
favorito, etc.
Variable cuantitativa
 Los valores son exclusivamente números.

6. Variable Cuantitativa
V.C. Directa
 Este subtipo de variable
solo puede formar u
número determinado
en un respectivo tramo,
por ejemplo, estado
civil, color favorito.
V.C. Continuo
 Este subtipo de variable
puede tomar tanto
valores como
queramos en un
determinado tramo por
ejemplo: las alturas de
personas contemplan
entre 1.7 y 1.8.

7. Frecuencia Absoluta y Relativa
 Recolecta los datos para que el estudio proceda a su
recuento para expresarlo de manera ordenada,
generalmente en forma ordenada como tablas. En las tablas
se muestra la frecuencia con que aparece cada dato.
FRECUENCIA ABSOLUTA
Se llama frecuencia absoluta
de un dato al número de
veces que ha salido ese
dato o resultado. La suma de
las frecuencias absolutas de
todos los datos que se han
obtenido en la encuesta o
estudio, ha de ser igual al
número total de datos.
FRECUENCIA RELATIVA
Se llama frecuencia relativa
de un dato al cociente entre
su frecuencia absoluta y el
número total de datos.
La suma de todas las
frecuencias relativas de los
datos de un estudio tiene que
ser igual a 1.

8. Gráficos Estadísticos
 Las representaciones gráficas permiten
captar de inmediato las características más
relevantes de una distribución de datos.
 Es frecuente realizar los datos obtenidos en
un estudio estadístico mediante gráficas
que relacionan las variables con sus
respectivas frecuencias
 Los modelos mas conocidos de
organización son los siguientes:

9. Variable Frecuencia Gráfico
Cualitativa Absoluta, Relativa,
Porcentaje
Diagrama de
barras, Gráfico de
sectores,
Pictograma
Cuantitativa
Discreta
Cualquier tipo Polígono de
frecuencia,
Diagrama de
barras, Gráfico de
sectores
Cuantitativa
Continua
Cualquier tipo Histograma,
Polígono de
frecuencia

10. Diagrama de Barras
Se utiliza para representar los caracteres cualitativos y
cuantitativos discretos.
 En el eje horizontal, o eje de abscisas, se representan
los datos o modalidades.
 En el eje vertical o de ordenadas, se representan las
frecuencias de cada dato o modalidad.
 Sobre el eje horizontal se levantan barras o
rectángulos de igual base (que no se superpongan)
cuya altura debe ser proporcional a la frecuencia
que representan.

11. HISTOGRAMA
Es un sistema de representación grafica en el que los
valores se organizan por intervalos. El histograma se
utiliza solo cuando la variable es continua.
Su construcción es similar a la del diagrama de barras a
diferencia de que los rectángulos de cada barra están
unidos.
En el histograma también se realiza el polígono de
frecuencia

12. EJERCICIO:
1) Determinar la amplitud de cada tramo
2) Determinar el numero total de individuos
3) Realizar el histograma
4) Realizar el polígono de frecuencia
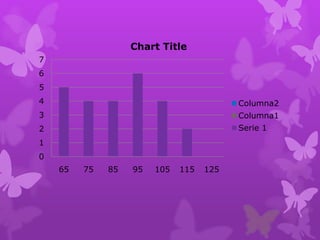
 Se realiza un estudio estadístico a una determinada
población obteniéndose los siguientes resultados:
INTERVALO FI
[65, 75] 5
[75, 85] 4
[85, 95] 4
[95, 105] 6
[105, 115] 4
[115, 125] 2

13. 0
1
2
3
4
5
6
7
65 75 85 95 105 115 125
Chart Title
Columna2
Columna1
Serie 1

14. DIAGRAMA DE SECTORES
 El diagrama de sectores se utiliza cuando queremos
representar frecuencias de cualquier tipo de
variables. Los datos de ubican en un sector circular.
La amplitud de cada sector circular viene dada por
la siguiente expresion:
Sa=Fi.360/ N Sa=Hi.360
 Un sector circular se define como el espacio
comprendido entre dos radios y su eje
correspondiente.

15. EJEMPLO:
 Queremos organizar la opinión de los alumnos de primer
año referente a las instalaciones deportivas de su
instituto, obteniendo los siguientes resultados: Determinar
1) variable, 2)hi y sci , 3) diagrama circular
Valoracion Fi
Muy buena 13
Buena 12
Regular 14
Mala 9
Muy mala 2
Hi SCI
0,26 93,6
0,24 86,4
0,28 100,8
0,18 64,8
0,04 14,4
1) Determinar la
variable
2) hi y sci
3) diagrama circular

16. DIAGRAMA CIRCULAR
Notas
Muy buena
Buena
Regular
Mala
Muy mala

17. PICTOGRAMA
 Es un tipo de representación grafica que se utiliza
para variables cualitativas, que consiste en graficar
para cada valor de la variable una figura
proporcional respectiva a la frecuencia absoluta.

18. MEDIDAS DE CENTRALIZACION
Son unos parámetros estadísticos que nos indican los valores mas
representativos de un conjunto de datos.
Las principales medidas de centralización son:
 Media aritmética
 Mediana
 Moda
Media Aritmética
La media aritmética de un conjunto de datos es el valor medio que los
representa. Su símbolo es x.
La media aritmética es un valor que esta entre el mayor y menor de un
conjunto de datos.
Pueden o no coincidir con los datos, además que puede ser un numero
decimal. Solo se puede obtener de datos cuantitativos.

19. Existen 3 formas de calcular la media aritmética:
1) Dividir la suma de los datos para el numero total de datos
2) Si los datos vienen dados en una tabla de frecuencia se
debe multiplicar a cada dato xi por su respectiva.
X=xifi+x2f2+x3f3…+xnfn x=xifi
N N
3) Si los datos vienen agrupados en intervalos, se calcula la
marca de clase de cada intervalo y ese valor pasa a ser xi y se
le suma y se utiliza la formula del paso anterior.
CALCULO DE LA MEDIA ARITMETICA:

20. EJEMPLO :
 Se han contenido las alturas en cm de los niños de
un instituto calcular la media de los datos.
Datos (xi) fi Xifi
160 7 1120
162 4 648
164 4 656
166 1 166
168 4 672
170 3 510
172 1 172
€ 24 3944
X=xifi/N
X=3944/24
X=164,33 CM//

21. Mediana:
Se define como el valor central de un conjunto de
datos. Se representa con Me, si el conjunto de datos es
impar la mediana es el valor central de ellos.
Valores Pares
1, 1, 1, 2, 2, 3, 4, 4, 5, 5
Valores Impares
1, 1, 2, 3, 4, 4, 5

22. Moda:
En un conjunto de datos es el valor que mas se repite
, es decir el de mayor frecuencia absoluta. Si conjunto
de datos tiene 2 valores de frecuencia absoluta, se
dice que se manifiesta una distribucion bimodal, si son 3
o mas valores es multimodal.

23. MEDIDAS DE DISPERSION
Indican las diferencias entre cada valor y la medida
aritmética de la distribución . Son parámetros que
muestran el nivel de disgregación de los datos en un
estudio estadístico.
Las primeras medidas de dispersión son:
 RECORRIDO Rec=x-xo
 DESVIACION D_xi-x
 VARIANZA DM=Efi|xi-x|/N
 COEFICIENTE DE VARIACION o=E fi(xi-x)/N

24. EJEMPLO:
Se realiza un estudio estadístico acerca de las
cantidades de libros por los estudiantes de 3 año de
bachillerato en el periodo de 1 año. Calcular todas
las medidas de centralización y de dispersión.
xi Fi xifi xifx Fi|xi-x| (xi-x) Fi(xi-
x)
0 2 0 -3.22 6.44 10.37 20.74
1 3 3 -2.22 6.66 4.93 14.79
2 5 10 -1.22 6.1 1.49 7.45
3 8 24 -0.78 1.76 0.05 0.4
4 8 32 1.78 6.24 0.61 4.88
5 3 15 2.78 5.34 3.17 9.51
6 2 12 3.78 3.34 7.73 15.46
7 1 7 4.78 3.78 14.29 14.29
32 103 41.88 87.52
X=3.22
Me=3
Mo=3^4(BI)
R=7
DM=1.31
O2=2.74
O=1.65
CN=0.51
D=3.78

25. MEDIDAS DE POSICION
Una medida de posicion es un valor de la variable que
nos ingforma del lugar que ocupa un dato dentro del
conjunto ordenado de valores.
Los principales medidas de posicion son:
 Cuartiles
 percantiles

26. GRACIAS
;)