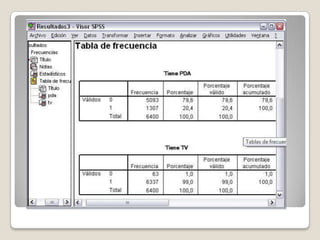
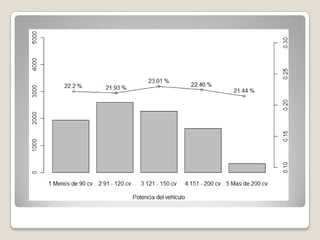
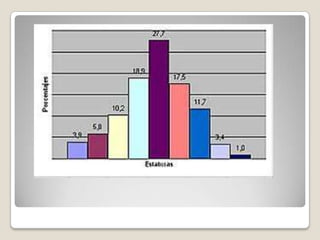
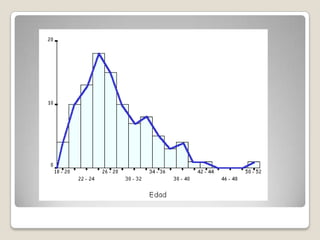
El documento proporciona una introducción a la estadística descriptiva. Explica que la estadística descriptiva provee herramientas para organizar, simplificar y resumir datos básicos a través de tablas, gráficos y medidas. Describe medidas de tendencia central como la media, mediana y moda, y medidas de dispersión como el rango, desviación estándar y varianza. También cubre representaciones gráficas de datos y medidas de posición.