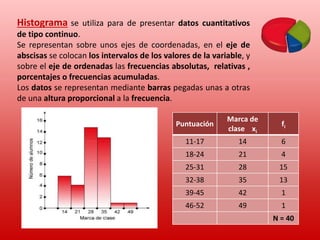
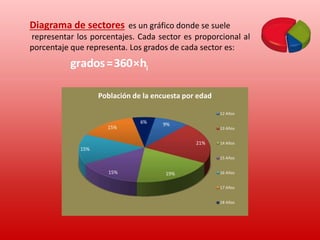
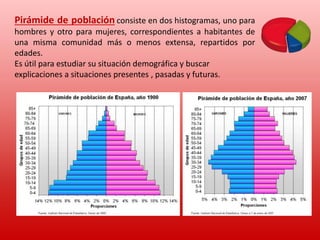
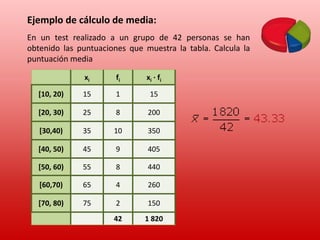
Este documento proporciona información sobre conceptos estadísticos básicos. Explica que la estadística se encarga de recopilar, clasificar y presentar datos para la toma de decisiones. Define conceptos como población, muestra, variable estadística, valor, recopilación de datos, clasificación de datos y presentación de datos. También describe diferentes tipas de variables estadísticas, métodos de recopilación de datos, tablas de frecuencias y gráficos estadísticos como diagramas de barras e histogramas.

2. Es aquella disciplina que se encarga
de la recopilación , clasificación,
presentación y descripción de
unidades de información
denominadas datos para una
adecuada toma de decisiones.

3. Población
es el conjunto de elementos sobre los cuales se va a
estudiar una determinada característica.
Muestra es una parte de la población.
Variable estadística:
el aspecto que se va a estudiar. Si se puede
medir se llama variable cuantitativa si no se pueden medir se llama
variable cualitativa.
Si la variable estadística toma un número determinado de valores se
llama variable discreta.
Si la variable estadística puede tomar cualquier valor entre dos valores
dados se llama variable continua.
Valor es cada uno de los distintos resultados que se pueden obtener
en un estudio estadístico.

4. RECOGIDA DE DATOS :
Planteado el test o encuesta oportuno , una vez elegido
el tema al que se quiere hacer el estudio estadístico, y
recogidos los datos que correspondan, el primer análisis
que realizaremos es el del tipo de variable que
pretendemos estudiar (Cualitativa o Cuantitativa;
Discreta o Continua).
Esto condicionará en gran medida su posterior
tratamiento.

6. CLASIFICACIÓN DE LOS DATOS :
Determinado el modo de agrupamiento de las
observaciones, procedemos a su recuento,
construyendo la tabla de frecuencias.
Posteriormente podremos visualizar tales frecuencias de
forma gráfica con el diagrama estadístico apropiado.
a) TABLA DE FRECUENCIAS
b) GRÁFICOS: diagrama de barras, histograma,
polígono de frecuencias, diagrama de sectores,
pictogramas, pirámides de población, climogramas,
etc.

7. Se a encuestado a un grupo de personas, queriendo conocer el numero
de habitantes en su vivienda.
DATOS
xi
Frecuencia
absoluta
fi
Frecuencia
absoluta
acumulada
Frecuencia relativa
Decimal
Fi
hi = fi
N
Porcentual
Frecuencia relativa
acumulada
Decimal
Porcentual
%i =100×hi
Hi
%Ai
5
6
6
0,0150
1,5 %
0,0150
1,5 %
6
48
54
0,1200
12 %
0,1350
13,5 %
7
95
149
0,2375
23,75 %
0, 3725
37,25 %
8
105
254
0,2625
26,25 %
0,6350
63,50 %
9
87
341
0,2175
21,75 %
0,8525
85,25 %
10
59
400
0,1475
14,75 %
1
100 %
1
100 %
N = 400

8. Se le pregunta a un grupo de personas, sobre los días que demora para
termina de leer una obra literaria.
[0, 5)
[5, 10)
[10, 15)
[15, 20)
[20, 25)
[25, 30)
[30, 35)
[35, 40)
[40, 45)
[45, 50)
xi
2.5
7.5
12.5
17.5
22.5
27.5
32.5
37.5
42.5
47.5
fi
1
1
3
3
3
6
7
10
4
2
N = 40
Fi
1
2
5
8
11
17
24
34
38
40
hi
0.025
0.025
0.075
0.075
0.075
0.150
0.175
0.250
0.100
0.050
1
Hi
0.025
0.050
0.125
0.200
0.2775
0.425
0.600
0.850
0.950
1
%
2.5
2.5
7.5
7.5
7.5
15
17.5
25
10
5
100
%Ai
2.5
5
12.5
20
27.5
42.5
60
85
95
100

9. 1
5
2
5
0
6
1
2
3
4
4
3
3
1
4
3
7
4
6
5
4
0
6
2
3
8
0
2
7
3
2
5
7
3
4
7
5
10
1
8
3
6
0
5
9
1
2
8
2
9
Cuando la cantidad de datos recopilados sea muy grande es
conveniente condensarlos en grupos denominados clases pero,
evitando perder demasiados detalles. Se elaboran tablas de
distribución de frecuencias a partir de los siguientes
elementos.

10. Tamaño ( n ) .- Es la cantidad de datos recogidos
En el ejemplo n =
Alcance ( A ) .- Es el intervalo cerrado que tiene por limites a los datos de menor y mayor
valor
En el ejemplo A = [
]
Rango ( R ) .- O amplitud , es la longitud del alcance
En el ejemplo : R = l ( A ) =
Número de clases ( K ).- Es la cantidad de grupos e intervalos y depende del criterio del
estadístico , aunque es usual utilizar como un primer valor aproximado el obteniendo por
la regla de sturges. K = 1 + 3 .3log (n)
En el ejemplo K = 1 +3.3log ( )
Ancho de clase ( Wi ).- Es la longitud de una clase. Si se desea anchos de clase iguales se
puede utilizar la siguiente relación: W = R/k
En el ejemplo W =
/
Frecuencia absoluta ( fi ).- Es la cantidad de datos que caen dentro de un clase .
En el ejemplo

11. Int / clase
( Fi )
[
, >
[
, >
[
, >
[
, >
[
,
]
Conteo
Frec. Absoluta
( fi )

12. 3ra Etapa : Presentación
En esta etapa, se elaboran tablas y gráficos más completos , a
partir de los siguientes elementos adicionales.
Frecuencia relativa ( hi ) .- Es la comparación establecida
entre la frecuencia absoluta y el tamaño de la muestra hi = /
Frecuencia absoluta acumulada ( Fi ) .- Es la suma de la
frecuencia absoluta correspondiente a una clase con todas las
precedentes.
Frecuencia relativa acumulada ( Hi ) .- Es la suma de la
frecuencia relativa a una clase como todas las precedentes.
Marca de clase ( xi ) .- Es un valor representativo de una clase
.Se calcula como la media aritmética de los limites del
intervalo

13. li
[
[
[
[
[
,
,
,
,
,
xi
>
>
>
>
]
fi
hi
Fi
Hi
(%)
xifi
ABSOLUTA
FRECUENCIA RELATIVA PORCENTUAL
FRECUENCIA RELATIVA ACUMULADA
FRECUENCIA
ACUMULADA
FRECUENCIA RELATIVA
FRECUENCIA ABSOLUTA
MARCA DE CLASE

14. LAS GRÁFICAS ESTADÍSTICAS
PERMITEN VISUALIZAR LA
INFORMACIÓN
CONTENIDA EN LAS TABLAS DE
MANERA RÁPIDA Y SENCILLA
DIAGRAMA DE BARRAS
HISTOGRAMA
EXISTEN MUCHOS TIPOS DE
GRÁFICAS ESTADÍSTICAS,
UNAS SE EMPLEAN CON
VARIABLES CUANTITATIVAS
Y OTRAS CON VARIABLES
CUALITATIVAS

15. Diagrama de barras se utiliza para de presentar datos
cualitativos o datos cuantitativos de tipo discreto.
Se representan sobre unos ejes de coordenadas, en el eje de
abscisas se colocan los valores de la variable, y sobre el eje de
ordenadas las frecuencias absolutas, relativas, porcentajes o
frecuencias acumuladas.
Los datos se representan mediante barras de una altura
proporcional a la frecuencia.
Grupo sanguíneo
Grupo
sanguíneo
6
B
4
AB
1
0
9
8
7
6
5
4
3
2
1
0
fi
A
fi 10
9
N = 20
A
B
AB
O

16. Histograma se utiliza para de presentar datos cuantitativos
de tipo continuo.
Se representan sobre unos ejes de coordenadas, en el eje de
abscisas se colocan los intervalos de los valores de la variable, y
sobre el eje de ordenadas las frecuencias absolutas, relativas ,
porcentajes o frecuencias acumuladas.
Los datos se representan mediante barras pegadas unas a otras
de una altura proporcional a la frecuencia.
Puntuación
Marca de
clase xi
fi
11-17
14
6
18-24
21
4
25-31
28
15
32-38
35
13
39-45
42
1
46-52
49
1
N = 40

17. Polígono de frecuencias se realiza para cualquier tipo
de variable. Es el polígono que se forma al unir los puntos
medios de las barras tanto en histogramas como en
diagramas de barras.

18. Diagrama de sectores es un gráfico donde se suele
representar los porcentajes. Cada sector es proporcional al
porcentaje que representa. Los grados de cada sector es:
grados =360×hi
Población de la encuesta por edad
12 Años
15%
6%
9%
13 Años
21%
14 Años
15%
15 Años
15%
19%
16 Años
17 Años
18 Años

19. Pictograma es un gráfico con figuras

20. Pirámide de población consiste en dos histogramas, uno para
hombres y otro para mujeres, correspondientes a habitantes de
una misma comunidad más o menos extensa, repartidos por
edades.
Es útil para estudiar su situación demográfica y buscar
explicaciones a situaciones presentes , pasadas y futuras.

21. Climograma son gráficas que representan la distribución de
precipitaciones y temperaturas a largo de un año en un lugar
determinado.

22. ANÁLISIS DE DATOS: Para este análisis se utilizan
los parámetros estadísticos:
a) Medidas de centralización
MEDIA, MEDIANA y MODA
b) Medidas de dispersión
RECORRIDO, DESVIACIÓN MEDIA,….
c) Medidas de posición
PERCENTILES y CUARTILES

23. Medidas de dispersión
RECORRIDO, DESVIACIÓN MEDIA,….
MEDIA ARITMÉTICA es el valor obtenido al sumar todos
los datos y dividir el resultado entre el número total de
datos.
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la
media es:
Evidentemente esta medida sólo se puede hallar para variables
cuantitativas.

24. Ejemplo de cálculo de media:
En un test realizado a un grupo de 42 personas se han
obtenido las puntuaciones que muestra la tabla. Calcula la
puntuación media
xi
fi
xi · fi
[10, 20)
15
1
15
[20, 30)
25
8
200
[30,40)
35
10
350
[40, 50)
45
9
405
[50, 60)
55
8
440
[60,70)
65
4
260
[70, 80)
75
2
150
42
1 820

25. MODA es el valor que tiene mayor frecuencia absoluta.
Se representa por Mo.
Se puede hallar para cualquier tipo de variable, aunque para variables
cuantitativas es poco útil.
La moda de la distribución:
2, 3, 3, 4, 4, 4, 5, 5
es Mo= 4
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y
esa frecuencia es la máxima, la distribución es bimodal o multimodal, es
decir, tiene varias modas.
1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9
Mo= 1, 5, 9

26. MEDIANA es el valor que ocupa el lugar central de todos los
datos cuando éstos están ordenados de menor a mayor.
La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana con pocos datos
1.
Ordenamos los datos de menor a mayor.
2.
Si la serie tiene un número impar de medidas la mediana es la
puntuación central de la misma.
2, 3, 4, 4, 5, 5, 5, 6, 6
3.
Me= 5
Si la serie tiene un número par de puntuaciones la mediana es la media
entre las dos puntuaciones centrales.
7, 8, 9, 10, 11, 12
Me= 9.5

27. Cálculo de la mediana para datos agrupados
fi
Fi
[60, 63)
5
5
[63, 66)
18
23
[66, 69)
42
65
[69, 72)
27
92
[72, 75)
8
100
100
Se divide N entre dos para ver
dónde está el centro
100/2 = 50
Se busca en la columna de Fi
dónde estaría 50.
Luego el valor o intervalo
mediano será:
Clase de la mediana: [66, 69)

28. RELACIÓN ENTRE MEDIA Y MEDIANA
a)
Si
b) Si
x=Me
, la distribución es completamente simétrica
x
los valores de
y
Me
son próximos, la distribución es
aproximadamente simétrica
c)
Si los valores de
asimétrica
x
y
Me
son poco próximos, la distribución es

29. ACTIVIDAD 1
a) A partir de las siguientes gráficas realiza la tabla de frecuencias y calcula
MEDIA, MEDIANA y MODA de cada una de las distribuciones.
b) Indica tipo de variable y tipo de gráfico en cada caso.
c) Indica cómo es simétricamente cada una de ellas.
Notas del control
Notas del control
Grupo A
Grupo B
5
5
4
4
3
3
2
2
1
1
0
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10

30. ACTIVIDAD 2
En el comedor de un instituto se da a elegir a su alumnado entre varios
primeros platos. El resultado de las distintas elecciones nos lo da el siguiente
gráfico.
a) Indica tipo de variable, y tipo de gráfica.
b) Sabiendo que se le ha preguntado a 240 personas, realiza la tabla
de frecuencias y calcula las medidas de centralización que más
sentido tengan.
23%
10%
Espaguetis
22%
Cocido
Lentejas
15%
Gazpacho
30%
Paella

31. Medidas de dispersión
RECORRIDO, DESVIACIÓN MEDIA,….
Recorrido es la diferencia entre los valores extremos, es decir, entre el
mayor valor y el menor
RECORRIDO = Valor mayor - Menor valor
Desviación Media es un parámetro asociado a la media; y es el promedio
( o media) de las distancias de los valores de todos los individuos a la media.
DM= suma de las distancias a x
N