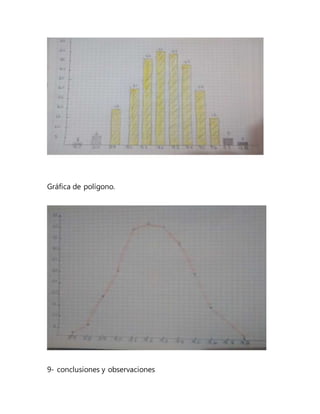
Este documento presenta un ejercicio estadístico sobre las ventas de tazas de café en una tienda de conveniencia durante 10 periodos de 30 días cada uno. Se elabora una tabla de distribución de frecuencias e interpreta los resultados. Se calculan medidas como la media aritmética, mediana, moda, desviación media, varianza y desviación estándar. Finalmente, se trazan gráficas como barras, polígono y cajas para ilustrar los datos y se presentan conclusiones sobre el ejercicio.

1. Estadística.
POFESOR: LIC. GERARDO EDGAR MATA ORTIZ
ALUMNO: ALEJANDRO ANTONIO IBARRA MUÑOZ
MATRICULA: 1410649
CARRERA: PROCESOS INDUSTRIALES
Fecha: 14

2. Índice:
Frases.................. 3
Ejercicio 2 ........... 4
Tabla de distribución de frecuencias....... 6.
Gráficas.............9
Conclusiones y observaciones........... 10
Bibliografía.............11

4. Frase.

5. Ejercicio 2
El director general de la empresa " Café Génesis" desea
determinar si es conveniente instalar un negocio especializado en
venta de café y sus complementos (galletas, pastel, etc.) en cierta
ubicación. La tabla adjunta muestra el número de tazas de café
vendidas en una tienda de conveniencia durante 10 periodos de
30 días cada uno. Los datos están ordenados conforme se
obtuvieron; la primera fila es el primer periodo de 30 días, la
segunda fila, el segundo periodo y así sucesivamente.
1- Con base en la información, explica cuál es la población.
R: La población son las tazas de café.
2- ¿se estudió la población completa? ¿O se trata solo de una
muestra?
R: una muestra porque solamente es una tienda de conveniencia.
3- ¿cuál es la variable de interés?

6. R: cuántas tazas de café se venden al día.
4- Determina el tiempo de variable y su escala de medición.
R: Es una variable cuantitativa porque se pueden medir los
resultados y es una variable continua porque son variables
continuos entre si.

7. Tabla de distribución de frecuencias.
5- Elabora la tabla de distribución de frecuencias e interpreta los
resultados

8. 6- Determina la mediana aritmética, mediana y moda y explica
sus significados.
Media aritmética: 92.41
Mediana: 51
Moda: 92
Media aritmética:
En matemáticas y estadística, la media aritmética (también llamada
promedio o simplemente media) de un conjunto finito de números
es el valor característico de una serie de datos cuantitativos objeto
de estudio que parte del principio de la esperanza matemática o
valor esperado, se obtiene a partir de la suma de todos sus valores
dividida entre el número de sumandos. Cuando el conjunto es una
muestra aleatoria recibe el nombre de media muestral siendo uno
de los principales estadísticos muestrales.
Mediana:
En el ámbito de la estadística, la mediana representa el valor de la
variable de posición central en un conjunto de datos ordenados.
Moda:

9. En estadística, la moda es el valor con una mayor frecuencia en
una distribución de datos.
7- calcular desviación media, varianza y desviación estándar.
Desviación media: 1.77973
Varianza: 1.45543
8- traza interpreta las gráficas siguientes: una grafica de barras con
la frecuencia absoluta, una gráfica circular con la frecuencia
relativa, una gráfica de polígono con la frecuencia relativa
acumulada, una gráfica de radial con los datos que consideras
apropiado y una gráfica de cajas y bigotes.
Gráfica de barras.

10. Gráfica de polígono.
9- conclusiones y observaciones

11. El trabajo estabsencillo pero a la vez laborioso ya que cuentas
ccon muchos datos que debes de tener en cuenta de no pasar
ninguno desapercibido ya que un solo error puede perjudicar todo
el problema.
Es fácil de entender los procedimientos y las formulas que nos
dan, aunque con muchos números uno se estresa pero es un
ejercicio muy practico que nos dan enseña a ser ordenadoa, a
tomar las estadísticas que nos pide el problema del café.

12. Bibliografía.
1
estadísticas para ingenieros y científicos. (Autor) William
navidi
2
probabilidad y estadística para ingeniería y ciencias (autor)
walpole-myers-myers
3
Estadística para administración y economía (autor) Anderson
sweeney Williams