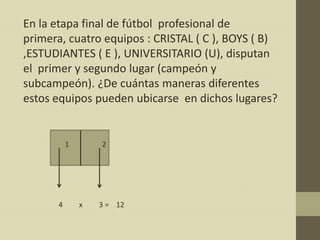
Este documento presenta conceptos básicos de conteo como permutaciones y variaciones. Explica las diferencias entre permutaciones con y sin repetición, así como variaciones. Proporciona ejemplos para ilustrar cómo calcular el número de formas posibles de organizar un conjunto de elementos teniendo en cuenta restricciones como el orden y la repetición. El objetivo es aplicar estas nociones de conteo a problemas relacionados con la ingeniería civil.

1. NOCIONES DE CONTEO
PERMUTACIONES
y
VARIACIONES
TITULACIÓN DE INGENIERÍA CIVIL
INTEGRANTES:
• George Stalin Chamba Chamba
• Adrian Fernando Contento Loyola
• Andrea Esthefanía Curipoma Viteri
• Cristhian Andrés Encalada Correa
• Carlos Alfonso Delgado Armijos

2. NOCIONES DE CONTEO
Principio de Adición:
Supongamos que algún evento E puede
ocurrir en m formas y un segundo evento F
puede ocurrir en n formas y supongamos
que ambos eventos no pueden ocurrir en
forma simultánea. Entonces E y F puede
ocurrir en m+n formas.

3. Ejemplo:
Supongamos que hay 8 profesores y 5 profesoras
que enseña en una clase de cálculo. ¿De cuántas
maneras un estudiante puede escoger un profesor
de cálculo?
8+5=13 maneras

4. Principio de Multiplicación:
Supongamos que un evento E puede
ocurrir en m formas e independiente de
este evento, un evento F puede ocurrir en
n formas. Entonces las combinaciones de
los eventos E y F pueden ocurrir en m*n
formas.

5. En la etapa final de fútbol profesional de
primera, cuatro equipos : CRISTAL ( C ), BOYS ( B)
,ESTUDIANTES ( E ), UNIVERSITARIO (U), disputan
el primer y segundo lugar (campeón y
subcampeón). ¿De cuántas maneras diferentes
estos equipos pueden ubicarse en dichos lugares?
1 2
4 x 3 = 12

6. • Un joven tiene 5 pantalones, 5 camisas y dos pares de
zapatos. ¿De cuantas maneras puede usar la camisa el
pantalón y los zapatos?
• Suponga que una biblioteca tenga 5 textos de historia, tres de
sociología, 6 de antropología y 4 de matemática. Encuentre el
número n de formas que el estudiante puede escoger.
a) Uno de los textos
b) Uno de cada tipo de texto
• De cuantas formas se pueden repartir dos premios entre 10
personas sabiendo que ambos premios
a) No se pueden conceder a la misma persona.
b) Se pueden conceder a la misma persona.

7. PERMUTACIONES
Permutaciones sin repetición
Denominamos permutaciones ordinarias o
sin repetición de n elementos, a cada uno de
los distintos grupos que pueden formarse de
manera que:
- En cada grupo entran todos los n
elementos.
- Un grupo se diferencia de otro únicamente
en el orden de colocación de los elementos.

8. A este número lo llamaremos factorial de n y lo
representaremos por n! , esto es:
Pn = n! =n.(n-1).(n-2)...3.2.1
Ejemplo:
Cuántas permutaciones se puede hacer de las tres
letras ABC.
3! = 1*2*3 = 6 permutaciones
Estas son:
ABC ACB BAC BCA CAB CBA

9. Una familia tiene 3 niños y 2 niñas
a) encuentre el número de formas en que ellos
pueden sentarse en una fila.
b) Cuántas formas hay si los niños desean
sentarse separados de las niñas.

10. Permutaciones con repetición.
Una permutación es una combinación en donde
el orden es importante. La notación para
permutaciones es P(n, r) que es la cantidad de
permutaciones de “n” elementos si solamente
se seleccionan “r”.

11. Encuentra el número n de permutaciones
distintas que pueden formarse con todas
las letras de cada palabra:
a) Those
b) Inusual
c) Sociological

12. Permutaciones circulares
Se utilizan cuando los elementos se han de ordenar "en
círculo", (por ejemplo, los comensales en una mesa), de
modo que el primer elemento que "se sitúe" en la muestra
determina el principio y el final de muestra.
PCn = Pn-1 = (n-1)!
10 personas se pueden sentar alrededor de una mesa
redonda (10-1)! formas distintas.

13. VARIACIONES
•

14. •

15. • Hallar los números que se pueden formar con 4 de los cinco dígitos
1,2,3,4,5.
a) Si estos no se pueden repetir en cada número
b) Si se pueden repetir
c) Si empiezan por 2
d) Si terminan en 25
• Hallar los números de 5 cifras que se pueden formar con los 10
dígitos 0,1,2,3,4,5,6,7,8,9 pudiendo estos repetirse.
a) Cuántos son
b) Si empiezan por 40
c) Si son impares
d) Si son divisibles para 5