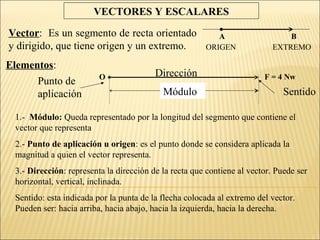
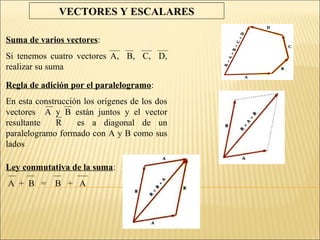
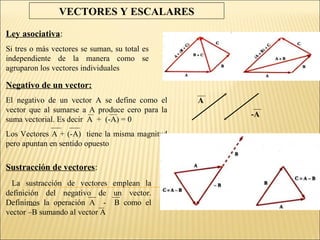
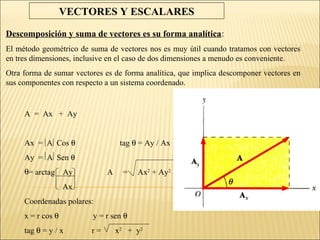
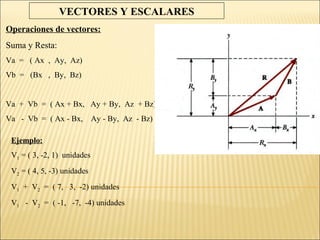
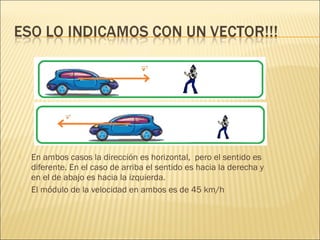
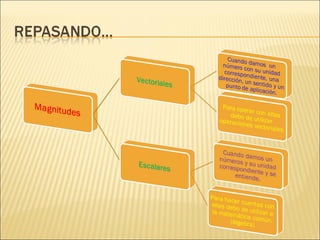
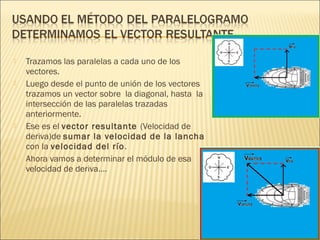
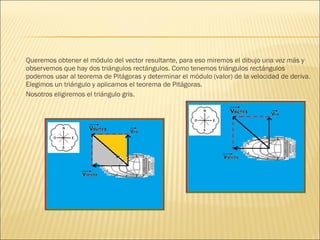
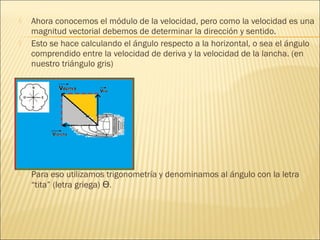
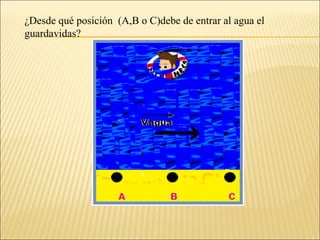
Para resolver este problema debemos analizarlo como un problema de vectores: - La corriente tiene una velocidad de 0,50 m/s hacia el este. Este es un vector. - El guardavidas nada a 1,5 m/s. Este también es un vector. - Para llegar lo más rápido posible al joven en peligro, el guardavidas debe nadar en la dirección opuesta a la corriente. - Si nada desde la posición A, su velocidad efectiva (vector resultante) sería la suma de los dos vectores. Esto lo llevaría en dirección

2. VECTORES Y ESCALARES
Tipos de Magnitudes:
Magnitudes escalares: Magnitudes vectoriales:
Son las que se caracterizan mediante Involucran un valor numérico y una
números reales en escala adecuada dirección, de modo que no se pueden
Tienen módulo, unidad y no poseen representar de forma completa por un
dirección número real.
Ejemplos: 30 ºC (temperatura), 50 Kg Posee magnitud como dirección.
(masa), 2 horas (tiempo), etc. Se denota con una K.
Ejemplos: Fuerza, velocidad, aceleración y
desplazamiento.
Cuando una partícula se mueve de A a B a lo
largo de una trayectoria arbitraria
representado por una línea punteada, su
desplazamiento es una cantidad vectorial
indicada por la flecha dibujada de A a B

3. VECTORES Y ESCALARES
Vector: Es un segmento de recta orientado A B
y dirigido, que tiene origen y un extremo. ORIGEN EXTREMO
Elementos:
O Dirección F = 4 Nw
Punto de
aplicación Módulo Sentido
1.- Módulo: Queda representado por la longitud del segmento que contiene el
vector que representa
2.- Punto de aplicación u origen: es el punto donde se considera aplicada la
magnitud a quien el vector representa.
3.- Dirección: representa la dirección de la recta que contiene al vector. Puede ser
horizontal, vertical, inclinada.
Sentido: esta indicada por la punta de la flecha colocada al extremo del vector.
Pueden ser: hacia arriba, hacia abajo, hacia la izquierda, hacia la derecha.

4. VECTORES Y ESCALARES
Igualdad de Vectores: “Dos vectores A y B pueden
definirse como iguales si tienen la misma magnitud y apuntan en
la misma dirección”, es decir que:
A=B ↔ A = B
Suma de Vectores: Cuando dos o más vectores se suman todas deben tener las
mismas unidades”. Ejemplo: no se pude sumar un vector velocidad a un vector
desplazamiento.
V + d  no se puede realizar
Reglas para sumar dos vectores por métodos geométricos:
Regla del triángulo: Para sumar un vector B al vector A, se dibuja
primero el vector A, con su magnitud representada en una escala
adecuada sobre un papel gráfico.
Luego se dibuja el vector B a la misma escala con su origen empezando
desde el punto de A.
Finalizando uniendo el origen del A con el extremo B

5. VECTORES Y ESCALARES
Suma de varios vectores:
Si tenemos cuatro vectores A, B, C, D,
realizar su suma
Regla de adición por el paralelogramo:
En esta construcción los orígenes de los dos
vectores A y B están juntos y el vector
resultante R es a diagonal de un
paralelogramo formado con A y B como sus
lados
Ley conmutativa de la suma:
A + B = B + A

6. VECTORES Y ESCALARES
Ley asociativa:
Si tres o más vectores se suman, su total es
independiente de la manera como se
agruparon los vectores individuales
Negativo de un vector:
El negativo de un vector A se define como el A
vector que al sumarse a A produce cero para la
-A
suma vectorial. Es decir A + (-A) = 0
Los Vectores A + (-A) tiene la misma magnitud
pero apuntan en sentido opuesto
Sustracción de vectores:
La sustracción de vectores emplean la
definición del negativo de un vector.
Definimos la operación A - B como el
vector –B sumando al vector A

7. VECTORES Y ESCALARES
Descomposición y suma de vectores es su forma analítica:
El método geométrico de suma de vectores nos es muy útil cuando tratamos con vectores
en tres dimensiones, inclusive en el caso de dos dimensiones a menudo es conveniente.
Otra forma de sumar vectores es de forma analítica, que implica descomponer vectores en
sus componentes con respecto a un sistema coordenado.
A = Ax + Ay
Ax = A Cos θ tag θ = Ay / Ax
Ay = A Sen θ
θ= arctag Ay A = Ax2 + Ay2
Ax
Coordenadas polares:
x = r cos θ y = r sen θ
tag θ = y / x r= x2 + y2

8. VECTORES Y ESCALARES
Vector en tres dimensiones:
V = ( Vx, Vy, Vz )
Se puede realizar analíticamente y geométricamente, como: Z
Componentes geométricos: módulo y ángulo: Y
Módulo V = Vx2 + Vy2 + Vz2
X
Si tenemos el siguiente vector
Z
θ V
Y
φ
X
Vz = V Cos θ Vx = V Sen θ Cos φ Vy = V Sen θ Sen φ

9. VECTORES Y ESCALARES
Vector en tres dimensiones: Cuando descomponemos un vector en sus componentes
algunas veces es útil introducir un vector de longitud unitaria en una dirección
determinada.
a
Ejemplo: a Asi el vector a puede escribirse
por ejemplo como:
Ua U=1
a = Ua a
A menudo es conveniente emplear vectores unitarios en las direcciones de los ejes de coordenadas
escogidos.En el sistema de coordenadas rectangulares ordinariamente se emplean los símbolos
especiales i, j y k, para vectores unitarios en las direcciones positivas de los ejes X, Y y Z
respectivamente
ax i, ay j , az k  Componentes Vectoriales
ax i, ay j , az k  Cantidades Vectoriales

10. VECTORES Y ESCALARES
Operaciones de vectores:
Suma y Resta:
Va = ( Ax , Ay, Az)
Vb = (Bx , By, Bz)
Va + Vb = ( Ax + Bx, Ay + By, Az + Bz)
Va - Vb = ( Ax - Bx, Ay - By, Az - Bz)
Ejemplo:
V1 = ( 3, -2, 1) unidades
V2 = ( 4, 5, -3) unidades
V1 + V2 = ( 7, 3, -2) unidades
V1 - V2 = ( -1, -7, -4) unidades

11. VECTORES Y ESCALARES
Multiplicación de vectores:
Tipos:
1.- ESCALAR . VECTOR = VECTOR
2.- VECTOR . VECTOR = ESCALAR (PRODUCTO ESCALAR)
3.- VECTOR x VECTOR = VECTOR (PRODUCTO VECTORIAL)
Producto de un Vector por un escalar:
El producto de un escalar K por un vector A se escribe K.A y se define un nuevo vector
cuya magnitud es K, veces mayor que la magnitud de A.
y
Ejemplo:
K.A
4 ( 3, 5, -2 ) = ( 12, 20, -8 )
Ay
A
Ax y

12.  La velocidad es una magnitud vectorial, no alcanza
con decir que se mueve un auto a 45 km/h. (eso es el
módulo!!)
 El auto puede venir hacia ti
 O el auto puede alejarse de ti

13.  En ambos casos la dirección es horizontal, pero el sentido es
diferente. En el caso de arriba el sentido es hacia la derecha y
en el de abajo es hacia la izquierda.
 El módulo de la velocidad en ambos es de 45 km/h

14.  La fuerza es una interacción entre por lo
menos dos cuerpos. No alcanza con decir que
Juan le hizo una fuerza de 400N a un
auto….esa fuerza la puede ejercer en
diferentes direcciones y sentidos!!

15.  Siempre que estés hablando de una magnitud
vectorial debes de dar;
 - Módulo.
 - Dirección.
 - Sentido.
 - Punto de aplicación.

17. Ejercicio
Un río fluye de sur a norte a 5.0 km/h. En
este río, una lancha va de este a oeste,
perpendicular a la corriente, a 7.0 km/h.
Vista por una águila suspendida en reposo
sobre la ribera, ¿que tan rápido y en que
dirección viaja la lancha?

18. Lo primero es realizar un bosquejo o dibujo de la situación.
Toma un papel y un lápiz , lee la letra del ejercicio y realiza el
bosquejo.
 En este momento puedes hacerte trampa y
avanzar en la diapositiva, ES COMO
HACERTE UNA TRAMPA AL SOLITARIO!!!!

20.  Lo primero es ubicar los puntos
cardinales, en nuestro sistema de
referencia.
 Luego debemos de indicar la velocidad
del agua y de la lancha.
 Un río fluye de sur a norte a 5.0 km/h.
 La lancha va de este a oeste,
perpendicular a la corriente, a 7.0 km/h

21. El río fluye de sur a norte a 5.0 km/h.
La lancha va de este a oeste a 7,0km/h.
 Análisis: Mientras la lancha avanza hacia el oeste, el río la lleva levemente hacia el norte.
 ¿Cómo determinamos la velocidad de la lancha?
 Lo que debemos hacer es sumar los vectores de velocidad. La velocidad final de la lancha es la
suma de la velocidad del río más la velocidad de la lancha. A esa velocidad final los marinos la
llaman velocidad de deriva.
 En lenguaje de ecuaciones:
El resultado final NO es sumar 7,0km/h + 5,0km/h …. ESTOS SON
VECTORES!!!!!!!!!!!!!!!!! Tienen módulo, dirección, sentido y punto de
aplicación.
LEER CONCEPTO DE VECTOR RESULTANTE

22.  Trazamos las paralelas a cada uno de los
vectores.
 Luego desde el punto de unión de los vectores
trazamos un vector sobre la diagonal, hasta la
intersección de las paralelas trazadas
anteriormente.
 Ese es el vector resultante (Velocidad de
deriva)de sumar la velocidad de la lancha
con la velocidad del río .
 Ahora vamos a determinar el módulo de esa
velocidad de deriva….

23.  Queremos obtener el módulo del vector resultante, para eso miremos el dibujo una vez más y
observemos que hay dos triángulos rectángulos. Como tenemos triángulos rectángulos
podemos usar al teorema de Pitágoras y determinar el módulo (valor) de la velocidad de deriva.
Elegimos un triángulo y aplicamos el teorema de Pitágoras.
 Nosotros eligiremos el triángulo gris.

24.  El teorema de Pitágoras dice que el
cuadrado de la hipotenusa es igual a
la suma de los catetos al cuadrado.
En una ecuación:
 Observando nuestro dibujo los
catetos son las velocidades del río y
de la lancha, y la hipotenusa es la
velocidad de deriva. Por lo tanto
sustituyendo esto, obtenemos;

25.  Ahora conocemos el módulo de la velocidad, pero como la velocidad es una
magnitud vectorial debemos de determinar la dirección y sentido.
 Esto se hace calculando el ángulo respecto a la horizontal, o sea el ángulo
comprendido entre la velocidad de deriva y la velocidad de la lancha. (en
nuestro triángulo gris)
 Para eso utilizamos trigonometría y denominamos al ángulo con la letra
“tita” (letra griega) ϴ.

27.  La velocidad de deriva es
de 8,6 km/k a 35,5° hacia
el norte respecto del oeste.
(horizontal).
 Los marinos acostumbran a
dar el ángulo respecto del
norte.

28. Estaba tranquilo en la playa, hasta que
ve a un joven en peligro.
Antes de entrar al agua observa la
situación:
La corriente tiene una
velocidad de 0,50m/s
hacia el este y el
guardavidas nada a una
velocidad de 1,5 m/s

29. ¿Desde qué posición (A,B o C)debe de entrar al agua el
guardavidas?