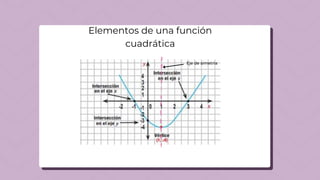
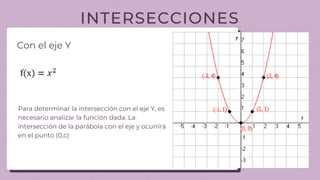
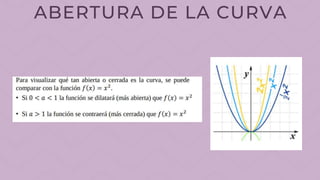
Este documento describe los elementos básicos de una función cuadrática de la forma f(x)=ax^2+bx+c. Explica que una función cuadrática tiene un eje de simetría, puede ser cóncava hacia arriba o abajo dependiendo del signo de a, y puede intersectar el eje y en (0,c) y el eje x en 0, 2 puntos o ninguno dependiendo del discriminante. También describe cómo una función cuadrática puede desplazarse horizontalmente cambiando b e verticalmente cambiando c.

2. OA:
Reconocer los elementos de
una función cuadrática.

3. Una función
cuadrática es de la
forma:
Con a≠0; a, b, c
perteneciente a los
reales (IR).
La función cuadrática
se puede graficar en
un plano cartesiano y
a esta gráfica(dibujo)
la llamaremos
PODEMOS OBSERVAR GRÁFICA DE LA FUNCIÓN CUADRÁTICA EN DISTINTAS
SITUACIONES Y OBJETOS DE NUESTRA VIDA COTIDIANA.

4. Elementos de una función
cuadrática
Eje de simetria

5. CONCAVIDAD

6. En en caso de las funciones cuadráticas, es
decir, de la forma:
La concavidad en este caso va a estar
determinada por el valor del signo de a.
Concavida
d

7. INTERSECCIONES
Con el eje Y

8. INTERSECCIONES
Con el eje Y
Para determinar la intersección con el eje Y, es
necesario analizar la función dada. La
intersección de la parábola con el eje y ocurrirá
en el punto (0,c)

9. INTERSECCIONES
Con el eje X
El discriminante nos otorga información muy importante
respecto a la gráfica de una función, pues nos permite saber si la
parábola intersecta el eje x y en cuantos puntos lo hace.

10. El vértice nos permite determinar el mínimo o máximo de la parábola.
• Si la parábola es cóncava hacia arriba, el vértice es un mínimo
• Si la parábola es abierta hacia abajo, el vértice es un máximo.
Considerando la función:
El vértice está dado por:
Y el eje de simetría está dado por:
VÉRTICE Y EJE DE SIMETRIA

11. ABERTURA DE LA CURVA Y
DESPLAZAMIENTO

12. ABERTURA DE LA CURVA

13. DESPLAZAMIENTO
HORIZONTAL
Si la función cuadrática esta de la forma 𝑓
(x)=(x+h)²
Se moverá ℎ unidades hacia la izquierda si 𝒉 > 𝟎.
Se moverá ℎ unidades hacia la derecha si 𝒉 < 𝟎.
Ejemplo:
f(x)=(x+4)². f(x)=(x-2)²

14. DESPLAZAMIENTO VERTICAL
Si la función cuadrática esta de la forma 𝑓 𝑥 = 𝑥²+ 𝑘.
• Se moverá k unidades hacia arriba si 𝒌 > 𝟎.
Por ejemplo: 𝑦 = 𝑥² + 𝟐
La función se ha desplazado 2 unidades hacia arriba.
• Se moverá k unidades hacia abajo si k < 0.
Por ejemplo: 𝑦 = 𝑥²− 𝟐
La función se ha desplazado 2 unidades hacia abajo.