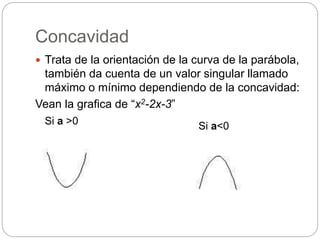
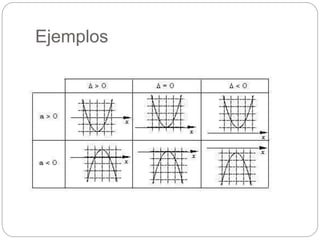
Este documento define y explica las características de las funciones cuadráticas. Explica que una función cuadrática tiene la forma de una ecuación cuadrática f(x)=ax^2 + bx + c. Luego describe las características clave de una función cuadrática como su gráfica, concavidad, intersecciones con los ejes x e y, determinante, eje de simetría y vértice. Finalmente, presenta ejemplos y ejercicios para practicar el cálculo de estas características.

1. Andrés Silva Palma
Función Cuadrática

2. Qué es una función?
 Una “función f” es una relación, tal que todo
elemento del conjunto de partida tiene imagen, y
esta es única.
Entrad
a:
1
2
3
4
Salida:
A
B
C
D
Función

3. ¿qué es una función cuadrática?
 Una función que posee la forma de una ecuación
cuadrática
 Ecuación cuadrática Función
cuadrática
f(x)= ax2+bx
+c

4. Características y componentes
 Grafica
 Concavidad
 Intersecciones con los ejes
 Determinante
 Eje se simetría y vértice

5. Grafica
 Las funciones en general se muestran en un
plano bidimensional llamado “Plano Cartesiano”,
en dicho plano cada punto reside una
coordenada de forma (x,y).

6. Concavidad
 Trata de la orientación de la curva de la parábola,
también da cuenta de un valor singular llamado
máximo o mínimo dependiendo de la concavidad:
Vean la grafica de “x2-2x-3”
Si a >0 Si a<0

7. Intersección con los ejes
 Se les conoce con este nombre a los puntos
donde la grafica de la función interseca a los ejes
Abscisa (x) y Ordenada (y), si bien se puede
apreciar grafica mente se puede calcular
mediante las siguientes formas.

8. Intersección con el eje Y
 Sea la función cuadrática: f(x)= ax2+bx+c,
cuando la parábola intercepta al eje Y , x = 0 y si
reemplazamos este valor en la ecuación,
obtenemos:
 y = a • 02 + b • 0 + c
 y = c
 Por lo tanto la intersección entre la parábola y el
eje Y es el punto (0,c)

9. Intersección con el eje X
 Análogo a la solución de la ecuación cuadrática
se puede encontrar con el uso de la misma
formula o con simple factorización, esto luego de
asignarle el valor y=0, pues:

10. Intersecciones con los ejes
 En resumen las intersecciones en un punto son:
 Eje y: (0,c)
 Eje x: (X1,0)(X2,0)

11. Determinante
 Este valor nos da cuantas intersecciones con el
eje x existen y si estas existen

12. Ejemplos

13. Eje se simetría
 Otra característica o elemento de la parábola es
su eje de simetría .
 El eje de simetría de una parábola es una recta
vertical que divide simétricamente a la curva; es
decir, intuitivamente la separa en dos partes
congruentes. Se puede imaginar como un espejo
que refleja la mitad de la parábola.

14. Eje de simetría
 Dicho eje (Recta) se calcula como:

15. Vértice
 Inserto en el eje de simetría se encuentra un
punto cúspide que ocupa el lugar mas alto o mas
bajo de la grafica de la función, este se le llama
vértice.Sus coordenadas son:
 En X: comparte esta con el eje de simetria
 En Y: Valor máximo o mínimo de la función.
 Entonces el vértice tiene coordenadas:

16. Usos comunes:

17. Ejercicios:
 Encuentre concavidad, determinante, eje de
simetria e intersección con el eje y de las
siguientes funciones.
 F(x)= x2-8x
 G(x)= x2+8x+16
 H(x)= x2+6x+20
 J(x)=-x2-2x-3