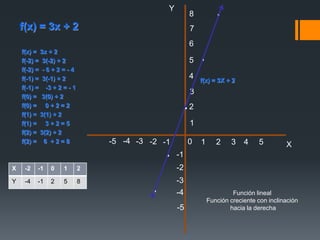
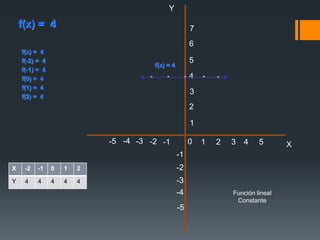
Este documento describe las funciones lineales y cuadráticas. Explica que una función cuadrática puede escribirse como ax2 + bx + c, y provee ejemplos. También describe cómo graficar una función cuadrática y cómo resolver ecuaciones cuadráticas usando la fórmula cuadrática. Además, presenta ejemplos de funciones lineales y cuadráticas y cómo evaluarlas y graficarlas.

1. FUNCIÓN LINEAL Y
CUADRÁTICA
UNIVERSIDAD DE ORIENTE
NÚCLEO DE MONAGAS
SECCIÒN DE MATEMÀTICA
Br. Ricardo Bermúdez
C.I 26.650.326
Sección 67

2. Una función cuadrática de variable “x” es aquella que
puede escribirse en la forma:
ax2 + bx + c = 0
Donde: a, b y c son números reales (a 0).
Ejemplo: 2x2 – 7x + 3 = 0 ( a = 2, b = 7, c = 3 )
DEFINICIÓN
FORMAS INCOMPLETAS
ax2 + bx = 0 Ejemplo: 3x2 – 2x = 0
ax2 + c = 0 Ejemplo: 2x2 – 32 = 0
ax2 = 0 Ejemplo: 9x2 = 0

3. Gráfica de una función cuadrática
Su gráfica es una
parábola cuya forma
dependerá de los
valores de a, b y c.

4. 4 -3 -2 -1 1 2 3 4 5 6 7
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
(h, k)
a > 0
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
(h, k)
a < 0
Sea V(h,k) el vértice:
f(h) = k es el mínimo valor de f cuando a>0
f(h) = k es el máximo valor de f cuando a<0

5. MÉTODO DE RESOLUCIÓN
POR LA FÓRMULA CUADRÁTICA (de Carnot)
a2
ac4bb
x
2


Dada la ecuación: ax2 + bx + c = 0, sus raíces pueden
calcularse mediante la fórmula
A la cantidad subradical: b2 – 4ac se le llama
discriminante y se representa por 
Es decir:  = b2 – 4ac

6. Ejemplo: Resolver 2x2 – 3x – 1 = 0
Resolución:
Identificamos los valores
de los coeficientes:
a = 2; b = – 3; c = –1 a2
ac4bb
x
2


Reemplazamos en:
)2(2
)1)(2(4)3()3(
x
2


Obtenemos:
4
173
x
4
173
x 21









 

4
173
;
4
173
.S.C
4
173
x


De donde:

7. Ejemplo: Resolver 4x2 – 12x + 9 = 0
Resolución:
Identificamos los valores
de los coeficientes:
a = 4; b = – 12; c = 9 a2
ac4bb
x
2


Reemplazamos en:
)4(2
)9)(4(4)12()12(
x
2


Obtenemos:
8
012
x
8
012
x 21




8
012
x


De donde:

8. EJERCICIOS DE FUNCIÓN CUADRÁTICA

9. 1.- Según la función Y= x² -8x + 12 , hallar su forma canónica, las intersecciones
con los ejes, vértice, eje de simetría y su gráfica.
Forma Canónica
Y= x² - 8x + 12
Y= (x² - 8x + 4² ) - 4² + 12
(x - 4 )² - 4² + 12
(x - 4 )² - 16 + 12
(x - 4 )² – 4
Y= (x - 4 )² – 4
Forma Canónica
Se ubica a través del trinomio cuadrado perfecto
a² – 2a.b + b²
(a - b ) ²
Nota: el + 4² y - 4² se obtienen de dividir 8 entre 2.
El 8 es el que acompaña a la x ósea 8x.
Se debe colocar el mismo número, pero con signos
diferentes para que no se modifique la función.
Intersecciones con los Ejes.
Y= x² - 8x + 12
Eje y (x = 0)
Y= x² - 8x + 12
Y= 0² - 8.0 + 12
Y= 0² – 0 + 12
Y = 12( 0; 12 )
x y
Intersección con el eje y.

10. Intersecciones con los Ejes.
Y= x² - 8x + 12
Eje X (y = 0) Y = x² - 8x + 12
0 = x² - 8x + 12
a b c
( 2; 0 ) ( 6; 0 )
x y x y
Intersección con el eje X.
Se toma la formula polinómica:
Y= ax² + bx + c
Donde:
a= 1 b= -8 c= 12

11. vértice
Y= (x - 4 )² – 4
Y= a (x - h )² + k
a = 1 - h = - 4
4 = h
h = 4
k = -4
Donde el vértice es : V= (h ; k)
V = (4 ; - 4)
Al graficarlo el valor de h está en las X
y el valor de K está en las y
Se aplica la formula:
Y= a (x - h )² + k
Eje de Simetría
X = h
X = 4
Gráfica
X
Y
8642
0
4
10
2
12
8
6
-2
-6
-2-8 -4-6
-4
-8
..
.
.Función Cuadrática
V= 4: -4)
Intersecciones: ((0 ; 12)
; (2 ; 0 ) y (6 ; 0)
Eje de Simetría: x = 4
Parábola que abre
hacia arriba porque
a > 0
vértice
Ejedesimetría

12. Función Lineal
f(x) = mx + b
m es la pendiente de la ecuación de la recta
b es la ordenada en el origen
Cuando m = 0, la función se denomina
“función constante”
f(x) = b

13. Función Lineal
f(x) = mx + b
-3 -2 -1 0 1 2 3
4
3
2
1
-1
-2
-3
b
Rfdom )(

14. EJERCICIOS DE FUNCIÓN LINEAL

15. f(x) = -2x + 3
f(x) = -2x + 3
f(-2) = -2(-2) + 3
f(-2) = 4 + 3 = 7
f(-1) = -2(-1) + 3
f(-1) = 2 + 3 = 5
f(0) = - 2(0) + 3
f(0) = 0 + 3 = 3
f(1) = -2(1) + 3
f(1) = -2 + 3 = 1
f(2) = -2(2) + 3
f(2) = -4 + 3 = -1
X -2 -1 0 1 2
Y 7 5 3 1 -1
X
Y
1 54320
5
4
3
2
1
7
6
-2
-1
-2 -1-5 -4 -3
-5
-4
-3
.
.
.
.
.
f(x) = -2x + 3
Función lineal
Función decreciente con inclinación
hacia la izquierda

16. f(x) = 3x + 2
f(x) = 3x + 2
f(-2) = 3(-2) + 2
f(-2) = - 6 + 2 = - 4
f(-1) = 3(-1) + 2
f(-1) = -3 + 2 = - 1
f(0) = 3(0) + 2
f(0) = 0 + 2 = 2
f(1) = 3(1) + 2
f(1) = 3 + 2 = 5
f(2) = 3(2) + 2
f(2) = 6 + 2 = 8
X -2 -1 0 1 2
Y -4 -1 2 5 8
X
Y
1 54320
5
4
3
2
1
7
6
-2
-1
-2 -1-5 -4 -3
-5
-4
-3
.
.
.
.
.
f(x) = 3X + 2
8
Función lineal
Función creciente con inclinación
hacia la derecha

17. f(x) = x + 4
f(x) = x + 4
f(-2) = -2 + 4
f(-2) = 2
f(-1) = - 1 + 4
f(-1) = 3
f(0) = 0 + 4
f(0) = 4
f(1) = 1 + 4
f(1) = 5
f(2) = 2 + 4
f(2) = 6
X -2 -1 0 1 2
Y 2 3 4 5 6
X
Y
1 54320
5
4
3
2
1
7
6
-2
-1
-2 -1-5 -4 -3
-5
-4
-3
.
.
.
.
.
f(x) = X + 4
8
Función lineal
Función creciente con inclinación
hacia la derecha

18. f(x) = 4
f(x) = 4
f(-2) = 4
f(-1) = 4
f(0) = 4
f(1) = 4
f(2) = 4
X -2 -1 0 1 2
Y 4 4 4 4 4
X
Y
1 54320
5
4
3
2
1
7
6
-2
-1
-2 -1-5 -4 -3
-5
-4
-3
.. ...
f(x) = 4
Función lineal
Constante