Las rectas notables de un triángulo son:
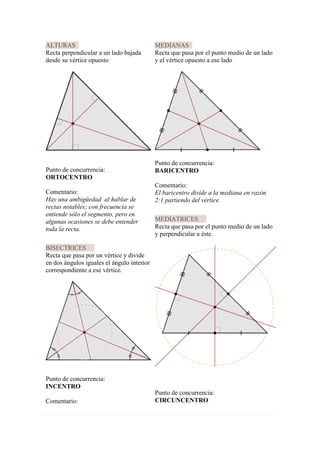
1) Mediatriz: recta perpendicular a un lado que pasa por su punto medio.
2) Mediana: recta que une un vértice con el punto medio del lado opuesto.
3) Altura: recta perpendicular a un lado que pasa por el vértice opuesto.
4) Bisectriz: recta que pasa por un vértice y divide el ángulo interior en dos partes iguales.