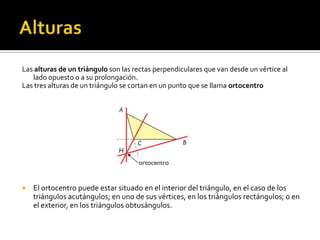
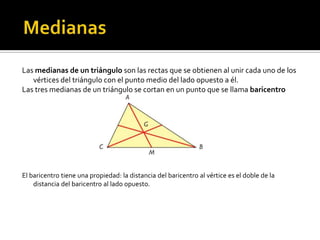
Este documento describe diferentes puntos y rectas notables de un triángulo como las medianas, mediatrices, alturas y bisectrices. Explica que las medianas se cortan en el baricentro, las alturas en el ortocentro, y las bisectrices en el incentro. También define cada uno de estos elementos geométricos y sus propiedades.

1. Matemáticas 3er. Grado de SecundariaEscuela Normal Superior del Sur de Tamaulipas.José Rogelio Mtz. Reyes.Lic. en Educación Secundaria.Especialidad: Matemáticas.

2. Formas GeométricasRectas y ángulos.

3. Puntos y rectas notables de un triangulo.En los triángulos hay una serie de rectas y puntos importantes. Las rectas son la mediana, la mediatriz, la altura y la bisectriz. Los puntos donde se cortan son el baricentro, el circuncentro, el ortocentro y el incentro, respectivamente.

4. AlturasLas alturas de un triángulo son las rectas perpendiculares que van desde un vértice al lado opuesto o a su prolongación.Las tres alturas de un triángulo se cortan en un punto que se llama ortocentroEl ortocentro puede estar situado en el interior del triángulo, en el caso de los triángulos acutángulos; en uno de sus vértices, en los triángulos rectángulos; o en el exterior, en los triángulos obtusángulos.

5. MedianasLas medianas de un triángulo son las rectas que se obtienen al unir cada uno de los vértices del triángulo con el punto medio del lado opuesto a él.Las tres medianas de un triángulo se cortan en un punto que se llama baricentroEl baricentro tiene una propiedad: la distancia del baricentro al vértice es el doble de la distancia del baricentro al lado opuesto.

6. MediatricesLas mediatrices de un triángulo son las rectas perpendiculares a sus lados que pasan por el punto medio.Se cortan en un punto que está a la misma distancia de los tres vértices del triángulo. Ese punto se denomina circuncentro.Con centro en el circuncentro, y radio la distancia del circuncentro a un vértice, dibujamos una circunferencia que pasa por los tres vértices; es la circunferencia circunscrita al triángulo.

7. BisectricesLas bisectrices de un triángulo son las rectas que dividen a sus ángulos en dos partes iguales.Las bisectrices de un triángulo se cortan en un punto llamado incentro.Con centro en el incentro, y radio la distancia de este punto a cualquiera de los lados del triángulo, se puede trazar una circunferencia tangente a los tres lados del triángulo: es la circunferencia inscrita.

8. Contesta correctamente:El baricentro es la intersección de las ......A) AlturaB) MedianasC)MediatricesD) BisectricesLa mediana es la recta que .....A) Une el punto medio de un lado con el vértice opuesto.B) Une el vértice y es perpendicular al lado opuesto.C) Une el vértice con el lado opuestoD) Es perpendicular a un lado por el punto medio

9. Se cumple que:A) El incentro de un triángulo siempre es interior al mismo.B) El baricentro de un triángulo puede ser exterior al mismo.C) El ortocentro de un triángulo siempre es interior al mismoD) El incentro de un triángulo puede ser exterior al mismoEl ortocentro es la intersección de las ......A) AlturaB) MedianasC)MediatricesD) Bisectrices

10. Traza en el siguiente triangulo sus bisectrices y señala el punto donde se intersecan, dando el nombre tambien de dicha intersección.

11. Traza en el siguiente triangulo sus mediatrices y señala el punto donde se intersecan, dando el nombre tambien de dicha intersección, además traza su respectiva circunferencia.