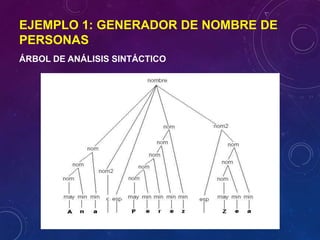
La gramática define las reglas de producción para generar cadenas válidas en lenguaje C. Define reglas para cabeceras de inclusión, funciones, tipos de variables, operadores básicos, cadenas de formato para entrada/salida, y más. Permite generar cadenas que representen código C válido como el ejemplo dado que incluye declaración de variables, entrada/salida, operaciones y retorno de función.

1. GRAMÁTICA DE
LIBRE CONTEXTO

2. ¿QUÉ ES LA GRAMÁTICA DE LIBRE
CONTEXTO O GLC?
• Gramática
• Permite definir un lenguaje mediante reglas que nos permiten generar o producir
cadenas de un lenguaje.
• Estas gramáticas son similares a las gramáticas de los lenguajes naturales, pero
mucho más restrictivas y sencillas.
• Los lenguajes libres del contexto son aquellos que pueden ser reconocidos por un
autómata de pila determinístico o no determinístico.

3. DEFINICIÓN FORMAL DE LA GRAMÁTICA
• G = (VN, VT, S, P) donde:
• VN (vocabulario no terminal): conjunto finito de símbolos que permiten
representar estados intermedios de la generación de las palabras del lenguaje
• VT (vocabulario terminal): conjunto finito de los símbolos que forman las
palabras del lenguaje. N ∩ T = ᴓ
• S ∈ VN (símbolo inicial o axioma): a partir del que se aplican las reglas de la
gramática para obtener las distintas palabras del lenguaje.
• P es el conjunto de reglas de producción (reglas de derivación o reglas de
reescritura) que permiten generar las palabras del lenguaje.

4. UN EJEMPLO 1 PARA CIERTAS
EXPRESIONES ARITMÉTICAS
G = (VN, VT, S, P)
• VT={ +, -, , *, ( , ), id }
• VN= { E}
• S=E
• P:
1. E→E+E 4. E→ E * E
2. E→E- E 5. E→ E / E
3. E→(E) 6. E → id
Nota: También los podemos ponerlo como una sola producción con alternativas
E → E + E | E - E | E E | E * E | ( E) | id

5. EJEMPLO 2: PARA UNA ORACIÓN DEFINIDA
• ORACIÓN SUJETO PREDICADO | PREDICADO
• SUJETO ARTÍCULO NOMBRE
• ARTICULO el | la
• NOMBRE casa | niño
• PREDICADO VERBO COMPLEMENTO
• VERBO corre | es
• COMPLEMENTO bien | obediente | bonita

6. BNF (BACKUS-NAUR FORM).
• Notación utilizada frecuentemente para escribir gramáticas de tipo 2 o libres
del contexto.
 Esta notación sigue las siguientes convenciones:
1. no terminales se escriben entre < >
2. terminales son cadenas de caracteres sin < >
3. en lugar de ® se utiliza :: = que se lee “se define como”
4. varias reglas del tipo
<A> :: = <B1>
<A> :: = <B2> Se pueden escribir como
… <A> :: = <B1> ½ <B2> ½ ... ½ <Bn>
<A> :: = <Bn>

7. DADA LA SIGUIENTE CADENA, PROPORCIONE LAS PRODUCCIONES
NECESARIAS EN GRAMÁTICA LIBRE DE CONTEXTO QUE GENERE
DICHA CADENA. PROPORCIONE UNA DEMOSTRACIÓN CON
DERIVACIÓN POR LA IZQUIERDA.
Cadena:
((a,a),a,(a))
Solución:
S -> (L) | a
L -> L,S | S
Gramática: G=(V,T,P,S) G=({S,L},{a,","},P,S)
Demostración:
S ==> (L) ==> (L,S) ==> (L,S,S) ==> (S,S,S) ==> ((L),S,S) ==>
==> ((L,S),S,S) ==> (S,S),S,S) ==> ((a,S),S,S) ==> ((a,a),S,S) ==>
==> ((a,a),a,S) ==> ((a,a),a,(L)) ==> ((a,a),a,(S)) ==> ((a,a),a,(a))

8. SEA LA GRAMÁTICA:
G=({S},{A,B},S,P), DONDE P={(S->ASB),(S->AB)}.
DETERMINAR EL LENGUAJE QUE GENERA
Solución:
S->aSb
S->ab
S==>aSb==>aaSbb==>aaaSbbb==>aaaaaSbbbbb ... ==>
==>a(n-1)Sb(n-1)==>anbn
L(G)={anbn / n>=1}

9. EJEMPLO 1: GENERADOR DE NOMBRE DE
PERSONAS
1. Hacer una gramática independiente del contexto (G.I.C), que genere nombres
de persona, mínimo un nombre y un apellido, máximo dos nombres y dos
apellidos. Cada nombre y apellido debe comenzar por mayúscula.
Nota: Se tiene en cuenta que Є=vacío; no se aceptan apellidos compuestos.
1. nombre → nom nom2 esp nom nom2
2. nom2 → esp nom │Є
3. nom → nom min │may
4. may → A│B│C│D│…│Z
5. min → a│b│c│d│…│z
6. esp → “ “

10. EJEMPLO 1: GENERADOR DE NOMBRE DE
PERSONAS
Ej: Ana Perez Zea
Resolución:
S= nombre (axioma inicial)
nombre= nom nom2 esp nom nom2
nom min Є esp nom min esp nom (3)(2)(3)(2)
nom min min Є esp nom min min esp nom min (3)(3)(3)
may min min Є esp nom min min min esp nom min min (3)(3)(3)
may min min Є esp nom min min min min esp may min min (3)(3)
may min min Є esp may min min min min esp may min min (3)
A n a P e r e z Z e a

11. EJEMPLO 1: GENERADOR DE NOMBRE DE
PERSONAS
ÁRBOL DE ANÁLISIS SINTÁCTICO

12. EJEMPLO 2: CÓDIGO EN LENGUAJE C
1. Hacer una gramática independiente del contexto (G.I.C), del siguiente código en C:
# include <stdio.h>
# include <stdio.h>
main()
{
int i, var1, var2, total;
clrscr();
printf(“Ingrese num 1:”);
scanf(“%d”,&var1);
printf(“Ingrese num 2:”);
scanf(“%d”,&var2);
total=var1+var2;
printf(“la suma de num 1 y num 2 es: ”,total);
getch();
Return 0;
}

13. EJEMPLO 2: CÓDIGO EN LENGUAJE C
Reglas de producción:
<CAB>::= <OPNUM><ESP>include
<ACA><LIB><CCA>
<LIB>::= stdio.h|conio.h
<OPNUM>::= #
<ACA>::= <
<CCA>::= >
<FUNC>::=<TIPOF><PR><AP><CP>
<ABLL><CELL>
<TIPOF>::= void|int|Є
<TIPOV>::= int|float|doublé
<PR>::= main
<AP>::= (
<CP>::= )
<FSENT>::= ;
<COMA>::= ,
<AMP>::= &
<VARS>::=<TIPOV><VAR><FSENT>
<VAR>::=<CADENA><COMA><VAR>|
<CADENA>
<FUNCR>::= <FR><AP><CP><FSENT>
<TIPFORM>::= %d|%i|%f|%s|%c
<FR>::= clrscr|getch|printf|scanf|return
<OPBASIC>::= +|-|*|/
<ABCO>::= “
<CECO>::= ”

14. EJEMPLO 2: CÓDIGO EN LENGUAJE C
<OPVAR>::=<VAR><OPBASIC><VAR>
<CADENA>::= <PALABRA><PALABRA2>
<PALABRA2>::=<ESP><CADENA>|Є
<PALABRA>::=<PALABRA><MIN>|<PALABRA><NUM>|<MAY>|<MIN>|<ESP>
<MAY>::= A|B|C|…|Z
<MIN>::= a|b|c|…|z
<NUM>::= 0|1|2|…|9
<FPRINTF>::=<FR><AP><ABCO><CADENA><CECO><CADENA2><CP><FSENT>
<CADENA2>::= <COMA><VAR>|Є
<FSCANF>::=<FR><AP><ABCO><TIPFORM><CECO><AMP><VAR><CP><FSENT>
<FRETURN>::=<FR><VAL><FSENT>
<VAL>::= 0|1
<ESP>::=“ “
<ABLL>::= {
<CELL>:: }