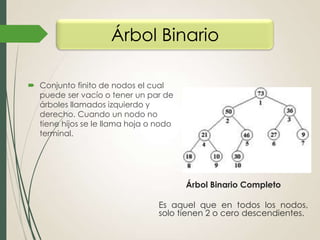
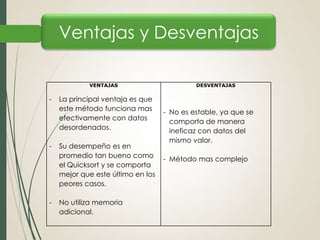
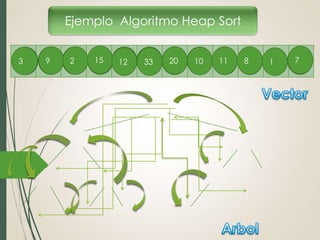
El documento explica el algoritmo de ordenamiento Heap Sort. Heap Sort funciona construyendo un montículo completo a partir de un arreglo y luego extrae el elemento raíz en cada iteración para obtener el arreglo ordenado. Primero se construye el montículo inicial, luego se intercambia la raíz con el último elemento y se restaura el montículo, repitiendo este proceso hasta ordenar todo el arreglo. Algunas ventajas son que funciona de manera efectiva con datos desordenados y su rendimiento promedio es similar a Quicksort.

1. Heap sort
Algoritmo de
Ordenamiento
LEIDY LINARES

2. Árbol Binario
 Conjunto finito de nodos el cual
puede ser vacío o tener un par de
árboles llamados izquierdo y
derecho. Cuando un nodo no
tiene hijos se le llama hoja o nodo
terminal.
Árbol Binario Completo
Es aquel que en todos los nodos,
solo tienen 2 o cero descendientes.

3. ¿Qué es un Head?
 Este head o montículo es un árbol binario donde todos los
padres son mayores que sus hijos.
 Este árbol binario tiene que ser completo, es decir, que debe
tener todos sus niveles llenos, excepto el ultimo y en este ultimo
nivel todos los hijos esta a un mismo lado ( por ejemplo a la
izquierda).

4. ¿Qué es Heap Sort?
 Es
un
algoritmo
ordenación
basado
comparaciones
elementos que utiliza
heap para ordenarlos.
de
en
de
un
 También podemos decir que
es
un
algoritmo
de
ordenación no recursivo, no
estable , con complejidad
computacional.

5. ¿Cómo Funciona Heap Sort?
 Este algoritmo consiste en almacenar todos los elementos del
vector a ordenar en un montículo y luego extraer el nodo que
queda como raíz en sucesivas iteraciones obteniendo el
conjunto ordenado. basa su funcionamiento en una propiedad
de los montículos, por la cual, la cima siempre
(depende
de como se defina) contendrá el mayor o menor elemento del
montículo.

6. Ventajas y Desventajas
VENTAJAS
-
-
-
La principal ventaja es que
este método funciona mas
efectivamente con datos
desordenados.
Su desempeño es en
promedio tan bueno como
el Quicksort y se comporta
mejor que este último en los
peores casos.
No utiliza memoria
adicional.
DESVENTAJAS
- No es estable, ya que se
comporta de manera
ineficaz con datos del
mismo valor.
- Método mas complejo

7. Características Heap Sort
 El árbol se llena de izquierda a derecha, lo que
implica que si algún (os) nodo (s) no está (n) en el
mismo nivel que el resto, éste (os) estará (n) entonces
lo más a la izquierda posible del árbol.

8. Algoritmo Lógico
º1
1. Se construye el montículo inicial a partir del arreglo original.
2. Se intercambia la raíz con el ultimo elemento del montículo.
3. El ultimo elemento queda ordenado.
4. El ultimo elemento se saca del montículo, no del arreglo.
5. Se restaura el montículo haciendo que el primer elemento baje a la
posición que le corresponde, si sus hijos son menores.
6. La raíz vuelve a ser el mayor del montículo.
7. Se repite el paso 2 hasta que quede un solo elemento en el montículo.

9. Ordenación por montículos – Heap
Sort

10. Ordenación por montículos – Heap
Sort

11. COMPARACION ALGORITMOS DE ORDENAMIENTO
ORDENAMIENTO
VENTAJAS
ALGORITMO
BURBUJA
Fácil de implementar
No requiere memoria adicional
ALGORITMO
INSERCIÓN
Fácil implementación
Requerimientos mínimos de memoria
ALGORITMO DE
SELECCIÓN
Fácil de implementar
No requiere memoria adicional
Realiza pocos intercambios
Rendimiento constante: poca diferencia entre
el peor y el mejor caso
ALGORITMO
SHAKE
Relativamente fácil de implementar.
No requiere memoria adicional
ALGORITMO SHELL
No requiere memoria adicional.
Mejor rendimiento que el método de Inserción
clásico
QUICK SORT
Muy rápido
No requiere memoria adicional.
HEAP SORT
Su desempeño es en promedio tan bueno
como el Quicksort y se comporta mejor que este
DESVENTAJAS
Muy lento
Muchas comparaciones
Muchos intercambios
Lento
Numerosas
comparaciones
Lento
Realiza numerosas
comparaciones
Realiza numerosas
comparaciones.
Realiza numerosos
intercambios.
Es inestable no mantiene
el orden relativo de los
registros.
Método mas complejo
Implementación un poco
más complicada
Método mas complejo
ESTABILIDAD
No intercambia registros
con claves iguales
No intercambia registros
con claves iguales. Por lo
tanto es estable
Puede que haya algo de
discrepancia pero esta
implementación parece
ser estable, puede verificar
esto ordenando un
conjunto de datos que
tenga un par de ellos con
la misma clave, el orden
relativo entre ellos es
conservado, pero algunos
autores dicen que no es
estable.
Es inestable no mantiene el
orden relativo de los
registros.
Es inestable no mantiene el
orden relativo de los
registros.

12. Ejemplo Algoritmo Heap Sort
3
9
2
15
12
33
20
10
11
8
1
7