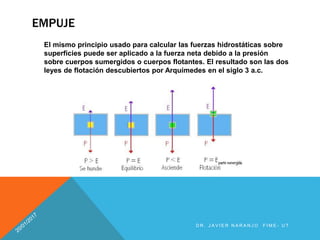
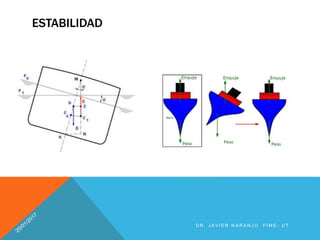
Este documento presenta conceptos clave sobre la flotabilidad y el empuje de Arquímedes. Explica que un cuerpo sumergido en un fluido experimenta una fuerza ascendente igual al peso del fluido desplazado, de acuerdo con el principio de Arquímedes. También define la estabilidad de cuerpos sumergidos y flotantes, y presenta ejemplos numéricos para ilustrar los conceptos.

1. F R A N C I S C O J AV I E R N A R A N J O
C H Á V E Z
FA C U LTA D D E I N G E N I E R Í A M E C Á N I C A
Y E L É C T R I C A , U N I D A D T O R R E Ó N
U N I V E R S I D A D A U T Ó N O M A D E
C O A H U I L A

2. D R . J A V I E R N A R A N J O F I M E - U T
EMPUJE
El mismo principio usado para calcular las fuerzas hidrostáticas sobre
superficies puede ser aplicado a la fuerza neta debido a la presión
sobre cuerpos sumergidos o cuerpos flotantes. El resultado son las dos
leyes de flotación descubiertos por Arquímedes en el siglo 3 a.c.

3. D R . J A V I E R N A R A N J O F I M E - U T
EMPUJE

4. D R . J A V I E R N A R A N J O F I M E - U T
PRINCIPIO DE ARQUÍMEDES (287-212 A.C.)
Un cuerpo sumergido en un fluido experimenta una fuerza ascensional
igual al peso del fluido desplazado.
Se puede sumar las fuerzas verticales
𝐹𝐵 =
𝑐𝑢𝑒𝑟𝑝𝑜
𝑝2 − 𝑝1 𝑑𝐴 = −𝛾 𝑧2 − 𝑧1 𝑑𝐴
= 𝛾(𝑣𝑜𝑙𝑢𝑚𝑒𝑛 𝑑𝑒𝑙 𝑐𝑢𝑒𝑟𝑝𝑜)

5. D R . J A V I E R N A R A N J O F I M E - U T
FLOTABILIDAD
Un cuerpo inmerso en un fluido experimenta una fuerza de flotación
vertical igual al peso del fluido que desplaza.
Un cuerpo flotando desplaza su propio peso in el fluido en el cual flota.
𝐹𝐵 = 𝐹𝑣 2 − 𝐹𝑣(1)
= 𝑝𝑒𝑠𝑜 𝑑𝑒𝑙 𝑓𝑙𝑢𝑖𝑑𝑜 𝑎𝑟𝑟𝑖𝑏𝑎 2 − 𝑝𝑒𝑠𝑜 𝑑𝑒𝑙 𝑓𝑙𝑢𝑖𝑑𝑜 𝑎𝑟𝑟𝑖𝑏𝑎 1
= 𝑃𝑒𝑠𝑜 𝑑𝑒𝑙 𝑓𝑙𝑢𝑖𝑑𝑜 𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡𝑒 𝑎𝑙 𝑣𝑜𝑙𝑢𝑚𝑒𝑛 𝑑𝑒𝑙 𝑐𝑢𝑒𝑟𝑝𝑜 𝑠𝑢𝑚𝑒𝑟𝑔𝑖𝑑𝑜

6. D R . J A V I E R N A R A N J O F I M E - U T
NO SOLO EN LÍQUIDOS
Los cuerpos también flotan en fluidos gases como los globos aerostáticos

7. D R . J A V I E R N A R A N J O F I M E - U T
ESTABILIDAD
Centro Gravedad CG Centro Empuje CB - Estabilidad cuerpo sumergido si
CG debajo CB - Equilibrio indiferente si CG coincide CB - Estabilidad de
Cilindros y esferas Flotantes si CG debajo CB - Estabilidad de Otros
cuerpos flotantes si aparece un momento adrizante cuando el CG y CB
se desalinean de la vertical

8. D R . J A V I E R N A R A N J O F I M E - U T
ESTABILIDAD

9. D R . J A V I E R N A R A N J O F I M E - U T
EJEMPLO 1
Si consideramos [1] tenemos que la masa del trozo de madera es: M = DV. Como la
densidad de la madera es 0,42 g/cm3, tomando en cuenta las medidas dadas en la
figura 73, tenemos que:
M = 0,42 g/cm3 · 10 cm · 10 cm · 8 cm
M = 336 g
Por lo tanto su peso es
Fg = mg = 0,336 kg · 10 m/s2 = 3,36 newton.
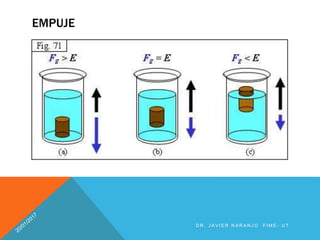
Esta fuerza debe ser igual al empuje que ejerce el agua, dado que la madera está en
equilibrio. Luego, considerando [6] podemos escribir:
3,36 newton = 1.000 kg/m3 · 10 m/s2 · 0,10 cm · 0,10 cm · y
de donde
y = 0,0336 m = 3,33 cm;
por lo tanto, como x + y = 8 cm, tenemos que
x = 4,64 cm.

10. D R . J A V I E R N A R A N J O F I M E - U T
EJEMPLO 2
Una pieza de aluminio con 1.00 kg de masa y 2 700 kg/m3 de densidad está
suspendida de un resorte. Si se sumerge por completo en un recipiente
de agua. Hallar la tensión en el resorte antes y b) después de sumergir
el metal

11. D R . J A V I E R N A R A N J O F I M E - U T
EJEMPLO 3
Un globo de plomo pb = 11.3x103 kg/m3 de radio R y espesor t ni flota ni se
hunde. Encuentre el grosor t.
Volumen plomo aprox. Vpb = 4pR2 t
suponiendo t << R.
Peso plomo Wpb = pbVpbg = 4pR2 tpbg
Peso agua desplazada Ww = 4pR3 wg/3
Igualando y despejando t se obtiene
t = 3mm

12. D R . J A V I E R N A R A N J O F I M E - U T
REFERENCIAS
Mataix, C. (1982). Mecánica de Fluidos y máquinas térmicas (Segunda ed.).
Mexico: Oxford University Press.
Mott, R. L. (2006). Mecánica de Fluidos 5ta Ed. México: Person Education
Inc.
White, F. M. (2003). Fluid Mechanics 5th Edition. New York: McGraw-Hill .
Mayori, A. ()
http://mecanica.umsa.edu.bo/libros/Mecanica%20Fluidos%204.pdf
Educarchile (2013) http://www.educarchile.cl/ech/pro/app/detalle?ID=133171
Pimentel, J.
http://www.jpimentel.com/ciencias_experimentales/pagwebciencias/pag
web/la_ciencia_a_tu_alcance_V/fisica/Exp_no_te_ahoges.htm