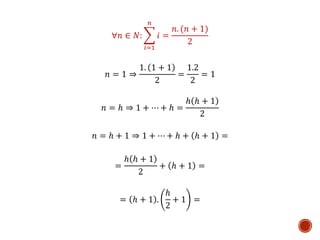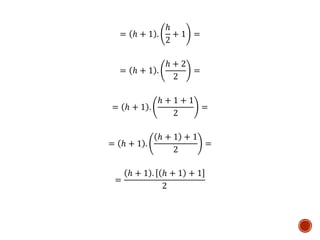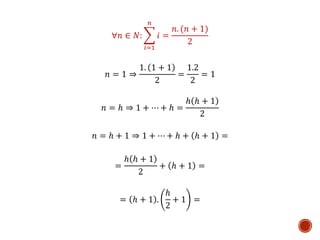
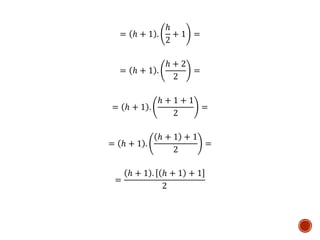
Este documento presenta tres pasos para probar una proposición para todos los números naturales mediante inducción matemática. Primero, se demuestra que la proposición es válida para 1. Luego, se asume que es válida para un número natural h y se prueba que también lo es para h+1. Finalmente, esto demuestra que la proposición es cierta para todos los números naturales.

1. Universidad Nacional del Nordeste
Facultad de Ciencias Exactas, Naturales y Agrimensura
Profesor Roberto Rodriguez

2.  Si queremos probar que una proposición es válida para todos
los números naturales.
 Corroboramos en principio que la proposición vale para 1.
 Luego suponiendo que vale para cualquier h natural, debemos
probar que vale para h+1.
 푃 푛 푒푠 푣푒푟푑푎푑푒푟표 ∀ 푛 ∈ ℕ 푠푖:
 푃 1 푒푠 푣푒푟푑푎푑푒푟표.
 푆푢푝표푛푖푒푛푑표 푞푢푒 푣푎푙푒 푃 ℎ
푑푒푏푒푚표푠 푝푟표푏푎푟 푞푢푒 푃 ℎ + 1 푒푠 푣푒푟푑푎푑푒푟표.

3. ∀푛 ∈ 푁:
푛
푖=1
푖 =
푛. (푛 + 1)
2
푛 = 1 ⇒
1. 1 + 1
2
=
1.2
2
= 1
푛 = ℎ ⇒ 1 + ⋯ + ℎ =
ℎ ℎ + 1
2
푛 = ℎ + 1 ⇒ 1 + ⋯ + ℎ + ℎ + 1 =
=
ℎ ℎ + 1
2
+ ℎ + 1 =
= ℎ + 1 .
ℎ
2
+ 1 =

4. = ℎ + 1 .
ℎ
2
+ 1 =
= ℎ + 1 .
ℎ + 2
2
=
= ℎ + 1 .
ℎ + 1 + 1
2
=
= ℎ + 1 .
ℎ + 1 + 1
2
=
=
ℎ + 1 . ℎ + 1 + 1
2

5. ∀푛 ∈ 푁:
푛
푖=1
2푖 − 1 = 푛2
푛 = 1 ⇒ 2.1 − 1 = 12
푛 = ℎ ⇒
ℎ
푖=1
2푖 − 1 = ℎ2
푛 = ℎ + 1 ⇒ 2.1 − 1 + ⋯ + 2ℎ − 1 + 2 ℎ + 1 − 1 =
= ℎ2 + 2 ℎ + 1 − 1 = ℎ2 + 2ℎ + 1 =
= ℎ + 1 2

6. ∀푛 ∈ 푁: 2|푛2 + 푛
푛 = 1 ⇒ 2 12 + 1 ⇒ 2 2
푛 = ℎ ⇒ 2|ℎ2 + ℎ ⇒ ℎ2 + ℎ = 2푘, 푘 ∈ 푁
푛 = ℎ + 1 ⇒ ℎ + 1 2 + ℎ + 1 =
= ℎ2 + 2ℎ + 1 + ℎ + 1 = (ℎ2+ℎ) + (2ℎ + 2) =
= 2푘 + 2 ℎ + 1 = 2 푘 + ℎ + 1
⇒ 2| ℎ + 1 2 + ℎ + 1