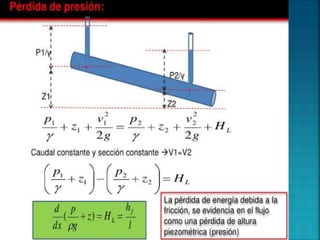
Este documento trata sobre las pérdidas hidráulicas en tuberías. Explica que existen dos tipos de flujo (a cielo abierto y a presión) y que se enfocará en el flujo a presión. Describe las pérdidas primarias y secundarias, y explica las ecuaciones de Darcy-Weisbach, Manning y Colebrook-White para calcular las pérdidas de carga debido a la fricción. También analiza cómo la rugosidad de la tubería afecta las pérdidas con el tiempo.

1. REALIZADO POR:
Jenny Rojas.
C.I:21.360.719
INSTITUTO UNIVERSITARIO
POLITÉCNICO SANTIAGO MARIÑO
AMPLIACIÓN MARACAIBO
ELECTIVA GESTIÓN TECNOLÓGICA
S.A.I.A.
SEDE POSTE NEGRO
INGENIERÍA CIVIL
Maracaibo, 11 de Mayo 2015

2. Hidráulicamente, se definen muy
claramente dos tipos de flujos:
Flujo a cielo abierto o en canales.
Flujo a presión o por tuberías.
En este capítulo vamos a estudiar el flujo
de agua por tuberías o conductos
cerrados, es decir cuando la presión es
mayor a la de la atmosférica; esta podría
estar dada por un tanque de carga,
sistemas de bombeo, etc.

6. Es la pérdida de energía dinámica del fluido debido
a la fricción de las partículas del fluido entre sí y contra
las paredes de la tubería que las contiene. Las pérdidas
pueden ser continuas, a lo largo de conductos
regulares, o accidentales o localizadas, debido a
circunstancias particulares, como un estrechamiento,
un cambio de dirección, la presencia de una válvula,
etc.
La pérdida de carga que tiene lugar en una
conducción representa la pérdida de energía de un
flujo hidráulico a lo largo de la misma por efecto del
rozamiento

7. Pérdidas primarias:
Se producen cuando el fluido se ponen contacto con la superficie
de la tubería. Esto provoca que se rocen unas capas con otras
(flujo laminado) o de partículas de fluidos entre sí (flujo
turbulento). Estas pérdidas se realizan solo en tramos de tuberías
horizontal y de diámetro constante.
Pérdidas secundarias:
Se producen en transiciones de la tubería (estrechamiento o
expansión) y en toda clase de accesorios (válvulas, codos). En el
cálculo de las pérdidas de carga en tuberías son importantes dos
factores:
Que la tubería sea lisa o rugosa.
Que el fluido sea laminar o turbulento

8.  PERDIDAS HIDRAULICAS
- Provocadas por el rozamiento de cada una de las
láminas del fluido entre si o con las paredes del
conducto y por las turbulencias que se forman durante
el flujo, son pérdidas directamente proporcionales a la
longitud del conducto, conocidas como perdidas reales
o pérdidas de longitud.
- Pérdidas que se concentran en determinados sitios de
conducto y producidas por diferentes obstáculos
localizados que provocan perturbaciones durante el
movimiento del líquido (su magnitud no depende de la
longitud del conducto, sino de la clase de obstáculos en
la tubería, se las conoce como pérdidas locales.

9.  En movimiento turbulento, los dos tipos de
pérdidas son proporcionales al cuadrado de las
velocidades medias del flujo del líquido en el
conducto.
FIGURA 1
DIAGRAMA ENTRE DOS SECCIONES DE TUBERÍA, DONDE SE MUESTRAN TODAS LAS LÍNEAS, LAS ALTURAS, LOS
EJES Y NIVELES DE REFERENCIA

10.  En la figura anterior se tiene un tramo de conducto a
presión por el cual s mueve un líquido real sin que se
presenten pérdidas locales, en consecuencia solo se
producen pérdidas de longitud.
La diferencia entre la energía total de la corriente en
las secciones I y II del conducto, define la magnitud de
la correspondiente pérdida.
En movimiento uniforme la gradiente hidráulica es igual
a la pendiente de la línea de presiones, en
consecuencia a más pendiente de la línea de energía,
hf (pérdida lineal) tiene una mayor magnitud.
La gradiente hidráulica se expresa: J=hf/L, relación
entre las pérdidas lineales y la longitud del conducto

12.  De conformidad con Darcy –Weisbach, la magnitud de
las pérdidas lineales está dada por:
 En donde:
f coeficiente adimensional de las resistencias
lineales
L longitud del conducto
D diámetro del conducto
v velocidad media del flujo
g gravedad
El coeficiente f depende de la viscosidad del líquido,
la velocidad media en el conducto, la rugosidad de las
paredes y el diámetro del conducto.

13.  En la práctica este coeficiente depende de dos
variables: el número de Reynolds Re y de la rugosidad
relativa e=k/d=rugosidad absoluta/diámetro del
conducto.
La rugosidad absoluta no es más que la altura media de
las salientes en las paredes del conducto expresada en
mm por ejemplo.
Cuando dos conductos tienen la misma rugosidad
absoluta pero distinto diámetro, la influencia de las
desigualdades en las paredes es mayor en el conducto
más delgado, por cuanto en el más ancho, los filetes
centrales del fluido que se desplazan más alejados de
las paredes no experimentan el frenado producido por
las rugosidades del conducto.

14.  En consecuencia, disponer de la rugosidad
absoluta k no nos permite una clara
orientación de lo que sucede dentro del
conducto, por lo que se hace necesario
conocer la rugosidad relativa e, para lo cual
nos ayudamos de los valores de la rugosidad
absoluta que se presenta en el siguiente
cuadro:

15.  RUGOSIDAD ABOLUTA
Clases de tubería k (mm)
Tubería de vidrio -0.0015
Tubería de acero nueva 0.02-0.15
Tubería de acero usada 0.50-0.40
Tubería de acero galvanizada 0.07-0.50
Tubería de hierro nueva 0.25-0.50
Tubería de hierro usada 1.00-1.50
Tubería de hierro recubierta
de asfalto 0.10-0.125
Tubería de cemento crudo 1.00-2.00
Tubería de hormigón 0.30-0.80

16. Únicamente para la zona de movimiento laminar
(Re<2320) el valor de f lo calculamos con la
fórmula f=64/Re y no podemos leer del gráfico de
Coolebrock-White, en consecuencia el coeficiente
de resistencia lineal, conocido también como
coeficiente de fricción f puede deducirse
matemáticamente para el caso de régimen laminar
y que aceptado por los investigadores hidráulicos
se ha adoptado a la ecuación de Poiseuille en la
forma indicada en líneas anteriores..
Para régimen turbulento no hay consensos,
habiéndose adaptado varias expresiones empíricas,
en donde la fórmula se expresa así:
f=f(Re, k/D)

17. Para régimen turbulento y tuberías lisas, pero con
Re>100.000 de estudios teóricos y ajustando
experimentalmente los coeficientes de Von Karman y
Prandtl dedujeron su primera ecuación:
1/√f=2log(Re√f)-0.8
Con tuberías rugosas, el coeficiente de resistencia
lineal f se calcula haciendo uso de fórmulas empíricas
que se basan en las siguientes consideraciones:
1.- Para Re<2000 ó Re>2000 en flujo laminar, la
rugosidad no influye en la pérdida de carga
f=f(Re)en tuberías lisas y rugosas

18. 2.- Si Re es elevado, f deja de ser función de
Re y responde a
f=f(k/D) rugosidad relativa
3.- Si Re tiene un valor intermedio
f=f(Re, k/D)
Fórmula universal de pérdidas de carga en
conductos industriales
1/√f=-2log(251/Re*√f+k/3.71*D)

19. La expresión más simple de la fórmula de
Manning se refiere al coeficiente de Chézy :
De donde, por substitución en la fórmula de
Chézy, , se deduce su forma más habitual:
ó

20. Siendo:
 n = coeficiente de rugosidad que se aplica en la
fórmula de Chézy:
 = radio hidráulico, en m, función del tirante
hidráulico h
 es un parámetro que depende de la rugosidad
de la pared
 = velocidad media del agua en m/s, que es
función del tirante hidráulico h
 = la pendiente de la línea de agua en m/m
 = área de la sección del fujo de agua
 = Caudal del agua en m3/s

21.  L: longitud de la tubería
 Q: caudal
 D: diámetrog
 Cf: factor de conversión

22. CARACTERÍSTICAS:
 Fórmula para calcular las pérdidas de energía por fricción.
 Fórmula empírica (desarrollada a partir de datos experimentales).
 Sólo es aplicable bajo condiciones muy especiales del flujo (por
ejemplo, bajo condiciones de flujo turbulento) y únicamente al agua
(bajo ciertas condiciones, a las cuales se llevó a cabo el experimento).
 Utiliza un factor de capacidad de carga C, el cual equivale a f en la
fórmula de Darcy – Weisbach. En la ecuación también hay un factor de
conversión Cf, el cual depende del sistema de unidades utilizado.
 Las pérdidas por fricción están dadas en función de muchas de las
mismas variables que en la fórmula de Darcy – Weisbach: longitud de la
tubería, diámetro del tubo, caudal.
 La rugosidad interna de la tubería está considerada dentro del
coeficiente de capacidad de carga C.
 Es una ecuación muy sencilla de manejar, pues depende de parámetros
fáciles de calcular. Esto constituye una ventaja de esta ecuación.

23. Debido a que las pérdidas de carga en las tuberías, es
función de la rugosidad de las mismas, se debe
analizar cómo varía ésta característica de la superficie
interna del tubo con respecto al tiempo de uso de las
mismas.
Algunos materiales, especialmente metálicos son
susceptibles de incrustaciones, especialmente de
carbonatos de calcio y de magnesio; lo que disminuye
su sección interna, y aumenta su rugosidad; y, por ende
su capacidad hidráulica.
Otros materiales, como el hormigón y el plástico, atrapan
las sustancias orgánicas contenidas en el agua,
especialmente las aguas servidas, lo que disminuye su
rugosidad.

24. Tabla del coeficiente de rugosidad de Manning
Material del revestimiento Ven Te Chow I. Carreteras4
Metal liso 0,010 -
Hormigón 0,013 1/60 - 1/75
Revestimiento bituminoso - 1/65 - 1/75
Terreno natural en roca lisa 0,035 1/30 - 1/35
Terreno natural en tierra con poca vegetación 0,027 1/25 - 1/30
Terreno natural en tierra con vegetación abundante 0,080 1/20 - 1/25