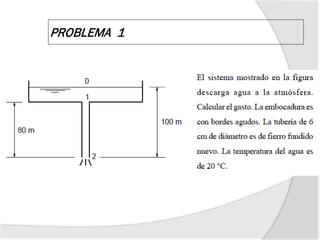
Este documento trata sobre conceptos básicos de mecánica de fluidos como la ecuación de energía, ecuación de Bernoulli y ecuación de continuidad. Explica las líneas de energía y piezométrica y los tipos de pérdidas de carga que ocurren en tuberías, incluyendo pérdidas por fricción y pérdidas locales en accesorios. Presenta fórmulas como la de Darcy-Weisbach para calcular pérdidas por fricción y ejemplos numéricos de cálculo de gastos en

1. ING. JUAN CABRERA
MECÁNICA DE FLUIDOS
PÉRDIDAS DE CARGA EN TUBERÍAS

2. CONCEPTOS PREVIOS
 Ecuación de la energía
 Ecuación de Euler
 Ecuación de Bernoulli
 Ecuación de continuidad

3. LÍNEA DE ENERGÍA Y LÍNEA PIEZOMÉTRICA

4. LÍNEA DE ENERGÍA Y LÍNEA PIEZOMÉTRICA
 La línea piezométrica (o de gradiente) indica por
medio de su altura sobre el eje de la tubería la
presión en cualquier punto de ella.
 En una tubería, o en tuberías de igual rugosidad y
diámetro, cuanto mayor es la pendiente o
inclinación de la línea de gradiente tanto mayor
será la velocidad del fluido.
 La línea de gradiente hidráulica indica por su
descenso vertical la energía perdida entre dos
secciones (para el movimiento uniforme).
 La gradiente hidráulica es recta para tuberías
rectas de sección transversal constante y para
tuberías cuya longitud sea aproximadamente igual

5. PÉRDIDAS DE CARGA(1)
 El flujo de un líquido en una tubería viene
acompañado de una pérdida de energía, que suele
expresarse en términos de energía por unidad de
peso de fluido circulante (dimensiones de longitud),
denominada habitualmente pérdida de carga.
 En el caso de tuberías horizontales, la pérdida de
carga se manifiesta como una disminución de presión
en el sentido del flujo.

6. PÉRDIDAS DE CARGA(2)
 La pérdida de carga está relacionada con otras
variables fluidodinámicas según sea el tipo de flujo,
laminar o turbulento.
 Además de las pérdidas de carga continuas (a lo
largo de los conductos), también se producen
pérdidas de carga locales en puntos concretos como
codos, ramificaciones, válvulas, etc.

7. PÉRDIDAS POR FRICCIÓN (1)
 Las pérdidas de carga continuas se deben a la
fricción y se calculan por medio de la fórmula de
Darcy-Weisbach:
donde: f: coeficiente de fricción
L: longitud de la tubería
D: diámetro de la tubería
V: velocidad media.
g: gravedad

8. PÉRDIDAS POR FRICCIÓN (2)
 El coeficiente de fricción depende de varios
parámetros:
- El número de Reynolds.
- La rugosidad de la tubería
- El régimen de flujo (laminar o turbulento)
- Comportamiento hidráulico de la tubería
- El espesor de la capa límite

9.  En el flujo laminar, el número de Reynolds es
bajo (menor a 2000) y todo el flujo dentro de la
tubería es laminar. Para el cálculo del coeficiente
de fricción se usa:
Re
64
=f
siendo Re = VD/ν. (V = velocidad media, D =
diámetro, ν = viscosidad cinemática).
PÉRDIDAS POR FRICCIÓN (3)

10.  En el flujo turbulento, la tubería puede
comportarse de dos maneras:
•Hidráulicamente Lisa
•Hidráulicamente Rugosa
PÉRDIDAS POR FRICCIÓN (4)

11.  Cuando el flujo es hidráulicamente liso, la capa
laminar d es mayor que la rugosidad ε,
“cubriéndola”. En este caso, tanto el número de
Reynolds como la rugosidad relativa ε/D influyen
en el cálculo de f.








+−=
f
Dk
f Re
51.2
7.3
/
ln86.0
1
PÉRDIDAS POR FRICCIÓN (5)

12. o Cuando el flujo es hidráulicamente rugoso, la
rugosidad e es mayor a la capa laminar d.
o En este caso, f sólo depende de la rugosidad
relativa ε/D.
14.1ln86.0
1
=





+
D
k
f
PÉRDIDAS POR FRICCIÓN (6)

15. ¿CÓMO DIFERENCIAR LISO DE RUGOSO? (1)

16. ¿CÓMO DIFERENCIAR LISO DE RUGOSO? (2)

17. Se tiene una tubería nueva de fierro fundido ( k =
0,00025 m) de 10” de diámetro. La longitud es de
1000 m. Conduce agua cuya viscosidad es de 10-6
m2/s. La pérdida de carga en el tramo considerado
es de 10 m. Calcular el gasto.
EJEMPLO 1

18. Calcular el diámetro que debe tener una tubería
nueva, de cemento enlucido ( k = 0,0004 m) para
conducir 2 m3/s. La viscosidad del agua es de 1,2 x
10-6 m2/s. La longitud de la tubería es de 1000 m. La
pérdida de carga admisible es de 25m.
EJEMPLO 2

19. Qué presión se requiere para impulsar 20 lps a lo
largo de una tubería lisa, horizontal, de 2” de
diámetro. La longitud del tramo es 300 m. La
viscosidad del agua es 10-6 m2/s.
EJEMPLO 3

20. EJEMPLO 4

21. FÓRMULA DE HAZEN-WILLIAMS

22. FÓRMULA DE HAZEN-WILLIAMS (2)

23.  Con este nombre se conocen las pérdidas
causadas por el flujo en un conducto forzado en
los codos, válvulas, salidas de reservorios,
entradas de reservorios, acoplamientos,
expansiones y en general en los accesorios que
se colocan en una tubería.
PÉRDIDAS LOCALES (1)

24.  Las pérdidas de carga locales se expresan
genéricamente en función de la altura de
velocidad en la tubería
PÉRDIDAS LOCALES (2)
g
V
KhK
2
2
=

25. 1. Entrada o embocadura
Corresponde genéricamente al caso de una
tubería que sale de un estanque.
PÉRDIDAS LOCALES (3)

26. PÉRDIDAS LOCALES (4)

27. PÉRDIDAS LOCALES (5)

28. 2. Entrega
Para este caso, k=1.
PÉRDIDAS LOCALES (6)

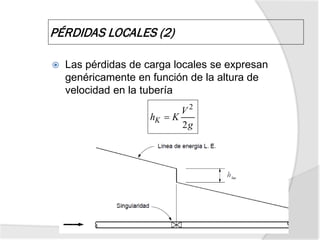
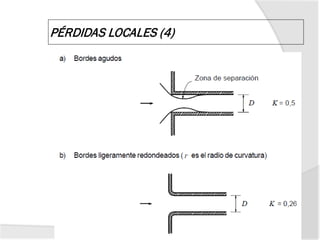
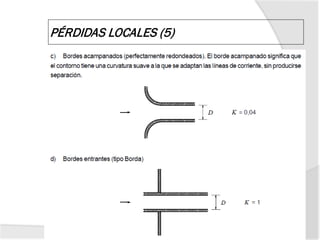
29. 3. Expansión
Esta pérdida es determinada teóricamente a partir
de las ecuaciones de la conservación de la
cantidad de movimiento y de continuidad.
22
2
1
])(1[
D
D
K −=
PÉRDIDAS LOCALES (7)

30. PÉRDIDAS LOCALES (8)

31. A2/A1 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Cc 0.624 0.632 0.643 0.659 0.681 0.712 0.755 0.813 0.892 1.0
hc = (1/ Cc –1)2 V2
2/(2g)
PÉRDIDAS LOCALES (9)
4. Contracción

32. Accesorio K
Válvula esférica (“tipo globo) – completamente abierta 10.0
Válvula angular (totalmente abierta) 5.0
Válvula “swing check” (completamente abierta) 2.5
Válvula de compuerta (completamente abierta) 0.19
“T” estándar 1.8
Codo estándar 90 ° 0.9
Entrada “cuadrada” o angular 0.5
Entrada de reservorio redondeada 0.01-0.05
Entrada de borda 0.8 – 1.0
PÉRDIDAS LOCALES (10)
5. Accesorios [K V2/(2g)]

33. PROBLEMA 1

34. PROBLEMA 2
Calcular el gasto en el problema 1 si se coloca en la
tubería una válvula de globo completamente
abierta.

35. PROBLEMA 3
Calcular cual debe ser el valor de la carga H (ver
figura) para que el gasto sea de 10 l/s. La tubería es
de fierro forjado, de 3” de diámetro. La longitud total
es de 75 m. La viscosidad del aceite es 0,1 poise y
su peso específico relativo es 0,9. La entrada es con
bordes agudos. El codo es a 90°. Calcular cada una
de las pérdidas de carga.

36. PROBLEMA 4
Se tiene una tubería de fierro fundido, asfaltado, de
6” de diámetro y 80 m de largo. La tubería arranca de
un estanque cuya superficie libre está 5 m por
encima del punto de descarga de la tubería. A lo
largo de la tubería hay dos codos standard de 90° y
una válvula de globo completamente abierta. La
embocadura es con bordes agudos. Calcular el
gasto. Considérese que la viscosidad cinemática del
agua es 10-6 m2/s.

37. PROBLEMA 5
Se tiene una tubería de fierro fundido de 6” de
diámetro y 80 m de largo. La tubería arranca de un
estanque que tiene 5 m de carga con respecto al
punto de desague. A lo largo de la tubería hay 2
codos standard de 90° y una válvula ( K = 10). La
embocadura es con bordes agudos. Calcular el gasto
(T = 20 °C).

38. PROBLEMA 6
Dos estanques cuya diferencia de nivel es de 25 m
están unidos por una tubería de 6” de diámetro y 1
550 m de longitud (asbesto - cemento, nuevo). La
viscosidad del agua es 10-6 m2/s. Calcular el gasto.

39. PROBLEMA 7
¿Cuál es la diferencia de nivel que debería existir
entre los dos estanques del problema anterior para
que el gasto sea de 50 l/s?.

40. ¿QUÉ APRENDIMOS HOY?