Este documento presenta los resultados de tres experimentos realizados en un laboratorio de mecánica de fluidos: 1) medición de pérdidas de carga en tuberías simples de diferentes materiales, 2) uso de un aforador de orificio, y 3) uso de un venturímetro. Los estudiantes midieron caudales, velocidades de flujo, pérdidas de carga, coeficientes de fricción y rugosidades para diferentes tuberías. Los cálculos incluyeron ecuaciones de Darcy-Weisbach, Colebrook-White y Barr para estimar la

1. PONTIFICIAUNIVERSIDAD CATÓLICADEL PERÚ
FACULTAD DE CIENCIAS E INGENIERÍA
LABORATORIO DE MECÁNICA DE FLUÍDOS
LABORATORIO N°5
(2014-2)
PÉRDIDAS EN TUBERÍAS SIMPLES/AFORADOR DE ORIFICIO/
VENTURÍMETRO
Horario: 060B Grupo : B
Fechade laboratorio: Martes de 11 a 1pm
Jefe de practica : Luis Samaniego
Alumno Codigo
Kevin Alejanro Vega Huayhua 20114477

2. TABLA DE CONTENIDO
1. PERDIDAS EN TUBERÍAS SIMPLES
1.1. OBJETIVOS
1.2. MARCO TEÓRICO
1.3. EQUIPOS Y PROCEDIMIENTO
1.4. CÁLCULOS Y RESULTADOS
1.5. COMENTARIOS Y POSIBLES FUENTES DE ERROR
1.6. CONCLUSIONES
2. AFORADOR DE ORIFICIO
2.1. OBJETIVOS
2.2. MARCO TEÓRICO
2.3. EQUIPOS Y PROCEDIMIENTO
2.4. CÁLCULOS Y RESULTADOS
2.5. COMENTARIOS Y POSIBLES FUENTES DE ERROR
2.6. CONCLUSIONES
3. VENTURÍMETRO
3.1. OBJETIVOS
3.2. MARCO TEÓRICO
3.3. EQUIPOS Y PROCEDIMIENTO
3.4. CÁLCULOS Y RESULTADOS
3.5. COMENTARIOS Y POSIBLES FUENTES DE ERROR
3.6. CONCLUSIONES

3. 1. PERDIDAS EN TUBERÍAS SIMPLES
1.1. OBJETIVOS
 Estudiar los efectos que se ocasionan en el caudal cuando se
tienen tuberías de diferente material.
 Determinar experimental y numéricamente la rugosidad de las
tuberías analizadas.
 Calcular el coeficiente de fricción “f” de Darcy-Weisbach y
compararlo con el encontrado en la bibliografía.
1.2. MARCO TEÓRICO
Fórmula Darcy-Weisbach:
Se utiliza para tuberías cortas (L/D < 2000) y establece que:
g
V
D
L
fhf
2
2

Donde:
hf = perdida de carga en metros
f = coeficiente de fricción
D = diámetro de la tubería
L = longitud de la tubería
V = velocidad media del flujo.
Para un flujo laminar (Re<2300):
Re
64
f
Para un flujo turbulento (Re>2300):
o Ecuación Colebrook-White: 






fd
k
f Re
51.2
71.3
log2
1
o Ecuación de Barr: 



 89.0
Re
1286.5
71.3
log2
1
d
k
f
Fórmula de Chezy:
Se utiliza con mayor frecuencia para canales aunque también se
aplica para tuberías cortas. Se establece que:
RSCV 
Donde:
V = velocidad media del flujo
R = radio hidráulico (
Pm
Am
R  )

4. S = pendiente de la línea de energía (
L
h
S f
 )
C = coeficiente de Chezy (















7
2
.12
log.18
k
R
C y
gRS


6.11
 )
Relación entre f y C:
Combinando las fórmulas de Darcy-Weisbach y la ecuación de
Chezy, podemos establecer la siguiente relación:
8g
C
f

1.3. EQUIPOS Y PROCEDIMIENTO
 Equipos y herramientas:
- Red de tuberías.
- Manómetros digitales.
- Agua.
- Cronómetro.
- Cinta teflón.
- Medidor volumétrico.
 Procedimiento:
- Se verificó que todas las válvulas se encuentren
cerradas, a excepción de la que fue objeto del estudio.
- Se comprobó que las llaves tanto de la línea de entrada
como la de salida de la red se encuentren abiertas y
que todos los conectores de presión tengan las válvulas
cerradas excepto aquellas en donde los manómetros
fueron colocados.
- Utilizando cinta de teflón se enroscó los dos
manómetros digitales en los puntos de interés.
- Se cerraron las válvulas conectoras en los puntos
donde se colocaron los manómetros y se encendió la
bomba.
- Haciendo uso del medidor volumétrico y de un
cronómetro se determinó el caudal que circulaba en el
sistema.
- Se abrieron las válvulas que transmiten la presión a
cada uno de los manómetros instalados

5. simultáneamente y se efectuaron las lecturas
correspondientes.
- Se cerraron las válvulas conectoras de presión abiertas
en el punto anterior y se apagó la bomba.
- Se desenroscaron los manómetros.
- Se abrieron algunas válvulas conectoras de presión
para acelerar el proceso por el cual todo el sistema se
vuelve a presión atmosférica. Se volvieron a cerrar
dichas válvulas
- Se repitió el procedimiento.
1.4. CÁLCULOS Y RESULTADOS
 Datos:
Longitud de la tubería: 3.67m
Viscosidad Cinemática del agua: 1*10-6m2/sg
Material
Φ Tubería
(mm)
Δ
Presiones
(psi)
Volumen
(lts)
Tiempo
medido (sg)
(a) PVC 50.8 1 100 16.37
(b) Fierro
Galvanizado 38.1 4 100 16.81
(c) PVC 38.1 2 100 16.66
 Cálculos:
- Para calcular el caudal real (Qr) se aplica: Qr =
Volumen/Área
Qra = 100/16.37 = 6.108 lps
Qrb = 100/16.81 = 5.949 lps
Qrc = 100/16.66 = 6.002 lps
- Para calcular la velocidad de flujo se aplica: V = Qr/Área
Va = (6.108/1000)/((π/4)*((50.8/1000)^2)) = 3.014 m/sg
Vb = (5.949/1000)/((π/4)*((38.1/1000)^2)) = 5.218 m/sg
Vc = (6.002/1000)/((π/4)*((38.1/1000)^2)) = 5.264 m/sg
- Para calcular el número de Reynolds, se utiliza:
𝑅𝑒 =
𝑉 ∗ 𝐷
𝜈

6. Rea = (3.014*(50.8/1000))/( 1*10-6) = 157683.2
Reb = (5.218*(38.1/1000))/( 1*10-6) = 198805.8
Rec = (5.264*(38.1/1000))/( 1*10-6) = 200558.4
- Para calcular la pérdida se aplica Bernoulli, de donde
se obtiene:
ℎ𝑓 =
𝛥𝑃𝑟𝑒𝑠𝑖𝑜𝑛𝑒𝑠
𝛾
hfa = (1*703.7014)/997.766 = 0.705 m
hfb = (4*703.7014)/997.766 = 2.821 m
hfc = (2*703.7014)/997.766 = 1.411 m
- Para hallar el coeficiente de fricción se utiliza la fórmula
de Darcy – Weisbach:
𝑓 =
2𝑔𝐷ℎ 𝑓
𝐿𝑉2
fa =
2∗9.81∗(
50.8
1000
)∗0.705
3.67∗3.0142 = 0.02108
fb =
2∗9.81∗(
38.1
1000
)∗2.821
3.67∗5.2182 = 0.02110
fc =
2∗9.81∗(
38 .1
1000
)∗1.411
3.67∗5.2642 = 0.01037
- Con la ecuación de Colebrook – White se halla la
rugosidad absoluta del conducto:
𝑘1 = (10
−
1
2√𝑓
−
2.51
𝑅𝑒√ 𝑓
) ∗ 3.71 ∗ 𝐷
La rugosidad relativa con: 𝜀1 =
𝑘1
𝐷
Y el coeficiente de Chezy:















7
2
.12
log.18
k
R
C ,
gRS


6.11

k1a = (10
−
1
2√𝑓
−
2.51
𝑅𝑒√𝑓
) ∗ 3.71 ∗ (50.8/1000) =0.0000472 m
k1b = (10
−
1
2√𝑓
−
2.51
𝑅𝑒√𝑓
) ∗ 3.71 ∗ (38.1/1000) =0.0000386 m
k1c = (10
−
1
2√𝑓
−
2.51
𝑅𝑒√𝑓
) ∗ 3.71 ∗ (38.1/1000)=-0.0000156 m

7. ε1a = 0.0000472/(50.8/1000) = 0.00093
ε1b = 0.0000386/(38.1/1000) = 0.00101
ε1c = -0.0000156/(38.1/1000) = -0.00041
δa = 0.0000024
δb = 0.0000014
δc = 0.0000019
C1a = 18 ∗ log (
12∗(
𝐷𝑎
4
)
𝑘1𝑎+
2
7
∗𝛿 𝑎
) = 63.050 √ 𝑚
𝑠𝑔⁄
C1b = 18 ∗ log (
12∗(
𝐷𝑏
4
)
𝑘1𝑏+
2
7
∗𝛿 𝑏
) = 62.405 √ 𝑚
𝑠𝑔⁄
C1c = 18 ∗ log(
12∗(
𝐷𝑐
4
)
𝑘1𝑐+
2
7
∗𝛿 𝑐
) = 69.8454 √ 𝑚
𝑠𝑔⁄
- También, con la fórmula de Barr se puede calcular la
rugosidad absoluta, y la rugosidad relativa se calcula
como se hizo en el paso anterior:
𝑘2 = (10
−
1
2√𝑓
−
5.1286
𝑅𝑒0.89
)∗ 3.71 ∗ 𝐷
k2a = (10
−
1
2√𝑓 𝑎 −
5.1286
𝑅𝑒 𝑎
0.89 ) ∗ 3.71 ∗ (50.8/1000) =
0.000045m
k2b = (10
−
1
2√𝑓 𝑏 −
5.1286
𝑅𝑒 𝑏
0.89) ∗ 3.71 ∗ (38.1/1000) =
0.0000371m
k2c=(10
−
1
2√𝑓 𝑐 −
5.1286
𝑅𝑒𝑐
0.89 ) ∗ 3.71 ∗ (38.1/1000)=
-0.0000121m
ε2a = k2a/(50.8/1000) = 0.0008858
ε2b = k2b/(38.1/1000) = 0.0009738
ε2c = k2c/(38.1/1000) = 0.0003176
C2a = 18 ∗ log (
12∗(
𝐷𝑎
4
)
𝑘2𝑎+
2
7
∗𝛿 𝑎
) = 63.417 √ 𝑚
𝑠𝑔⁄
C2b = 18 ∗ log (
12∗(
𝐷𝑏
4
)
𝑘2𝑏+
2
7
∗𝛿 𝑏
) = 62.712 √ 𝑚
𝑠𝑔⁄
C2c = 18 ∗ log(
12∗(
𝐷𝑐
4
)
𝑘2𝑐+
2
7
∗𝛿 𝑐
) = 71.9135 √ 𝑚
𝑠𝑔⁄
 Resultados:

8. Tubería
Qr
(lps)
V.
Flujo
(m/s
g)
Re
Pérdidas(m)
Darcy-
Weisbac
h f
Colebrook-White Barr
Chezy C
((m^1/2)/s)
K1(m) ε1 K2(m) ε2
con
K1
con K2
a 6.108 3.014 157683.2 0.705 0.02108 0.0000472
0.0000
024
0.0000
45 0.0008858
63.0
5
63.417
b 5.949 5.218 198805.8 2.821 0.0211 0.0000386
0.0000
014
0.0000
371 0.0009738
63.4
05
62.712
c 6.002 5.264 200558.4 1.411 0.01037 -0.0000156
0.0000
019
-
0.0003
176 -0.0000121
69.8
454
71.913
1.5. COMENTARIOS Y POSIBLES FUENTES DE ERROR
 La rugosidad no puede ser negativa, el hecho de que uno
de los resultados haya sido negativo puede ser
consecuencia de las fuentes de error a mencionar.
 La rugosidad no es uniforme en toda la tubería por lo cual
el cálculo de rugosidades resulta una rugosidad promedio.
 En las medidas del diámetro y de la longitud puede existir
un error humano.
 Cuando se mide el caudal por medio del medidor
volumétrico y del cronometro no existe una precisión y el
error humano puede ser apreciable en el cálculo del
caudal, lo que generaría errores en los posteriores cálculos
(velocidad del flujo, número de Reynolds).
1.6. CONCLUSIONES
 Las variaciones en los valores de las rugosidades
absolutas halladas con la fórmula de Colebrook y con la
fórmula de Barr es casi despreciable.
 Asimismo, los valores de los coeficientes de Chezy son
aproximadamente iguales, el único que varía es en la
última tubería.
 Por ambos métodos, el de Colebrook o Barr, obtenemos la
misma rugosidad, por lo que es correcto usar cualquiera de
las fórmulas.
 Los valores hallados de rugosidad son altos comparados
con los que se dan en tablas (0,0015 mm para el PVC),

9. esto se dio por los errores en la toma de datos de las
presiones.
 La rugosidad de la tubería de PVC es menor que la de la
tubería del mismo diámetro de fierro, lo que indica que el
PVC es menos rugoso que el fierro galvanizado.
 Se puede llegar a la conclusión de que la rugosidad
depende tanto del material como del diámetro de la
tubería.

10. 2. AFORADOR DE ORIFICIO
2.1. OBJETIVOS
 Determinar el coeficiente de descarga experimentalmente.
2.2. MARCO TEÓRICO
Se utiliza la ecuación de Bernoulli:
g
VP
g
VP
22
2
22
2
11

 .
Coeficiente de contracción del orificio: 𝐶𝑐 =
𝐴2
𝐴0
Por continuidad: 𝐴1 ∗ 𝑉1 = 𝐴2 ∗ 𝑉2
Combinando ambas ecuaciones:
𝑉2 =
√
2𝑔( 𝑝1 − 𝑝2)
𝛾 ∗ [1 − 𝐶 𝐶
2
∗ (
𝐷 𝑜
𝐷1
)
4
]
Por el área del chorro: 𝐴2 = 𝐶2 ∗ 𝐴0
𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜 = 𝐶𝑐 ∗ 𝐴0 ∗
√
2𝑔( 𝑝1 − 𝑝2)
𝛾 ∗ [1 − 𝐶 𝐶
2
∗ (
𝐷 𝑜
𝐷1
)
4
]
Por la relación entre caudales teóricos y caudales reales:
𝑄𝑟𝑒𝑎𝑙 = 𝐶 𝑣 ∗ 𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜
Se obtiene:

11. 𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜 = 𝐶 𝑑 ∗ 𝐴 𝑜 ∗
√
2𝑔( 𝑝1 − 𝑝2)
𝛾 ∗ [1 − (
𝐷 𝑜
𝐷1
)
4
]
donde Cd es el coeficiente de descarga e incluye los efectos de la
velocidad y la contracción.
2.3. EQUIPOS Y PROCEDIMIENTO
 Equipos y herramientas:
- Red de tuberías con Φ=27mm.
- Cronómetro.
- Manómetros.
- Bomba.
- Válvulas.
- Medidor volumétrico.
 Procedimiento:
- Primero se verificó que todo el caudal pase por la
tubería que se iba a estudiar, para ello se abrieron y
cerraron las llaves necesarias.
- Se comprobó también que las válvulas de todos los
conectores de presión estuviesen cerradas, todas
excepto en las que se iba a colocar los manómetros.
- Se enroscó cuidadosamente los manómetros digitales
en los dos puntos en los que se mediría la presión, si
fuera necesario se usó cinta de teflón.
- Se cerraron las válvulas conectoras de los puntos en
donde se colocaron los manómetros y se encendió la
bomba.
- Se determinó el caudal con ayuda del medidor
volumétrico y el cronómetro. Se abrieron al mismo
instante las válvulas conectoras de los dos puntos en
cuestión y se midieron las presiones registradas.
- Se cerraron las válvulas conectoras y se apagó la
bomba. Se desenroscaron los manómetros.
- Se repitió el procedimiento cambiando de accesorio.
2.4. CÁLCULOS Y RESULTADOS
 Datos:

12. Volumen Medido (lts) Tiempo Medido (sg) Pérdidas (m) Φ Tuberías Φ Orificio
300 49.22 18.1 50.8 27
300 48.4 19.58 50.8 27
300 47.11 0.38 50.8 27
 Cálculos:
- El caudal real se calcula dividiendo el volumen entre el
tiempo:
Q1 = 300/49.22 = 6.095 lps
Q2 = 300/48.4 = 6.198 lps
Q3 = 300/47.11 = 6.368 lps
- El coeficiente de descarga se calcula despejando la
ecuación:
𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜 = 𝐶 𝑑 ∗ 𝐴 𝑜 ∗ √
2𝑔 ( 𝑝1−𝑝2)
𝛾∗[1−(
𝐷 𝑜
𝐷1
)
4
]
; ℎ𝑓 =
𝑝1−𝑝2
𝛾
Cd1 =
𝑄1
0.00057∗
√
2∗9.81∗37.75
(1−(
27
50.8
)
4
)
= 0.544
Cd2 =
𝑄2
0.00057∗
√
2∗9.81∗33.79
(1−(
27
50.8
)
4
)
= 0.532
Cd3 =
𝑄2
0.00057∗
√
2∗9.81∗33.79
(1−(
27
50.8
)
4
)
= 3.756
 Resultados:
Volumen
mediddo
(lts)
Tiempo
medido (sg)
Pérdidas
(m)
Φ Tuberías Φ Orificio Qr (lps) Cd
300 49.22 18.1 50.8 27 6.095 0.544
300 48.4 19.58 50.8 27 6.198 0.532
300 47.11 0.38 50.8 27 6.368 3.756

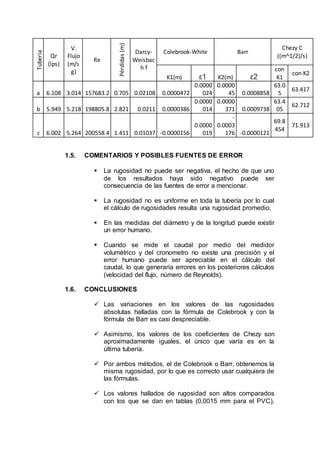
13. 2.5. COMENTARIOS Y POSIBLES FUENTES DE ERROR
 La única fuente de error apreciable sería la toma de
presiones en el manómetro, y podría incluirse también la
aplicación de la fórmula, el cambio de unidades o
redondeos que puede llevarnos a cometer algún error.
2.6. CONCLUSIONES
 Se observa que el coeficiente de descarga del orificio
aumenta cuando el caudal también aumenta; y, mientras
menor sean las pérdidas, mayor será el coeficiente de
descarga.
3. VENTURÍMETRO
3.1. OBJETIVOS
 Determinar los coeficientes de descarga Cd de los
venturímetros indicados.
3.2. MARCO TEÓRICO
Un estrechamiento provoca un cambio en la velocidad y en
consecuencia una variación de la presión estática. Aplicando la
ecuación de Bernoulli:
𝑝1
𝛾
+
𝑉1
2
2𝑔
=
𝑝2
𝛾
+
𝑉2
2
2𝑔
Por continuidad: 𝐴1 ∗ 𝑉1 = 𝐴2 ∗ 𝑉2
Combinando ambas ecuaciones:
𝑉2 =
√
2𝑔( 𝑝1 − 𝑝2)
𝛾 ∗ [1 − (
𝐷2
𝐷1
)
4
]
Por el área del chorro:

14. 𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜 = 𝐴2 ∗
√
2𝑔( 𝑝1 − 𝑝2)
𝛾 ∗ [1 − (
𝐷2
𝐷1
)
4
]
Por la relación entre caudales teóricos y caudales reales:
𝑄𝑟𝑒𝑎𝑙 = 𝐶 𝑑 ∗ 𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜
Se obtiene:
𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜 = 𝐶 𝑑 ∗ 𝐴2 ∗ √
2𝑔( 𝑝1 − 𝑝2)
𝛾 ∗ [1 − (
𝐷2
𝐷1
)4]
3.3. EQUIPOS Y PROCEDIMIENTO
 Equipos:
- Venturímetro con D1 = 54 mm y D2 = 35 mm.
- Manómetros.
- Válvulas.
- Cinta de teflón.
- Medidor volumétrico.
- Cronómetro.
 Procedimiento:
- Primero se comprobó que las llaves de entrada y salida
estuviesen abiertas de modo que circule el agua sólo
por la tubería en estudio.
- Se comprobó que los conectores de presión tengan las
válvulas cerradas excepto aquellas en las cuales se
colocarán los manómetros las cuales deberán estar
abiertas.
- Se enroscó cuidadosamente los manómetros digitales
en los dos puntos en los que se mediría la presión, si
fuera necesario se usó cinta de teflón.
- Se cerraron las válvulas conectoras de los puntos en
donde se colocaron los manómetros y se encendió la
bomba.
- Se determinó el caudal con ayuda del medidor
volumétrico y el cronómetro. Se abrieron al mismo
instante las válvulas conectoras de los dos puntos en
cuestión y se midieron las presiones registradas.
- Se cerraron las válvulas conectoras y se apagó la
bomba. Se desenroscaron los manómetros.

15. 3.4. CÁLCULOS Y RESULTADOS
 Datos:
Diámetro mayor de los venturímetros: 54 mm
Diámetro menor de los venturímetros: 35 mm
 Cálculos:
- Cálculo del caudal real: Qr = Volumen/Tiempo
Q1r = 300/48.45 = 6.211 lps
Q2r = 300/47.20 = 6.356 lps
Q3r = 300/48.90 = 6.135 lps
- Área (diámetro menor): A2 = (π/4)*(0.054^2) =
0.000962m2
- Cálculo del caudal teórico:
𝑄𝑡𝑒ó𝑟𝑖𝑐𝑜 = 𝐴2 ∗ √
2𝑔( 𝑝1−𝑝2)
𝛾∗[1−(
𝐷2
𝐷1
)
4
]
; ℎ𝑓 =
𝑝1−𝑝2
𝛾
Q1t = (𝐴2 ∗ √
2∗9.81∗0.97
[1−(
35
54
)
4
]
) ∗ 1000 = 4.757 lps
Q2t = (𝐴2 ∗ √
2∗9.81∗1.45
[1−(
35
54
)
4
]
) ∗ 1000 = 3.125 lps
Q2t = (𝐴2 ∗ √
2∗9.81∗1.45
[1−(
35
54
)
4
]
) ∗ 1000 = 4.789 lps
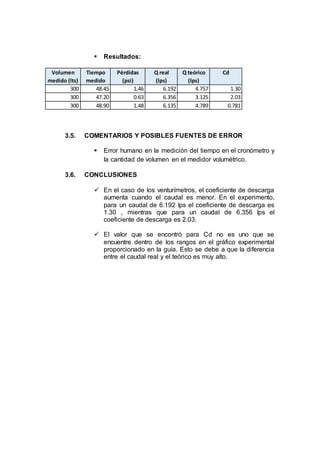
- Coeficiente de descarga: Cd = Qreal/Qteórico
Cd1 = Q1r/Q1t = 1.30
Cd2 = Q2r/Q2t = 2.03
Cd2 = Q2r/Q2t = 0.781
Diámetro mayor del vent. 54.0 (mm)
Diámetro menor del vent. 35 (mm)
Pesoespecíficodel agua : 1000 kg/m3

16.  Resultados:
Volumen Tiempo Pérdidas Q real Q teórico Cd
medido (lts) medido (psi) (lps) (lps)
300 48.45 1.46 6.192 4.757 1.30
300 47.20 0.63 6.356 3.125 2.03
300 48.90 1.48 6.135 4.789 0.781
3.5. COMENTARIOS Y POSIBLES FUENTES DE ERROR
 Error humano en la medición del tiempo en el cronómetro y
la cantidad de volumen en el medidor volumétrico.
3.6. CONCLUSIONES
 En el caso de los venturímetros, el coeficiente de descarga
aumenta cuando el caudal es menor. En el experimento,
para un caudal de 6.192 lps el coeficiente de descarga es
1.30 , mientras que para un caudal de 6.356 lps el
coeficiente de descarga es 2.03.
 El valor que se encontró para Cd no es uno que se
encuentre dentro de los rangos en el gráfico experimental
proporcionado en la guía. Esto se debe a que la diferencia
entre el caudal real y el teórico es muy alto.