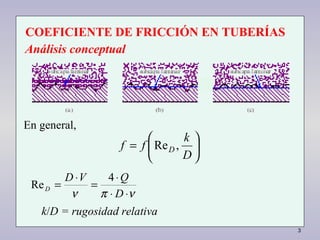
1. El documento presenta ecuaciones para calcular las pérdidas de carga en tuberías circulares, incluyendo la ecuación de Darcy-Weissbach y la relación entre el coeficiente de fricción y el número de Reynolds.
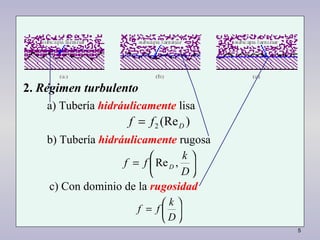
2. Se describen los regímenes laminar y turbulento y cómo se ve afectado el coeficiente de fricción. También se analizan tuberías lisas e irregulares.
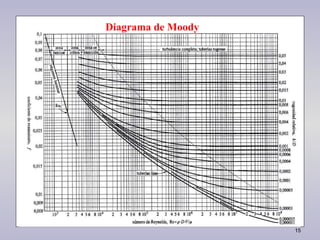
3. Se presentan ecuaciones matemáticas como las de Colebrook y Karman-Nikuradse para calcular el coeficiente de f