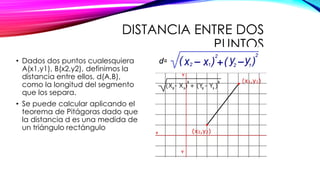
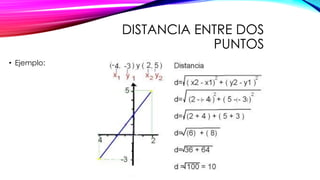
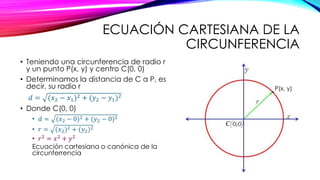
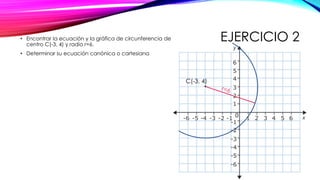
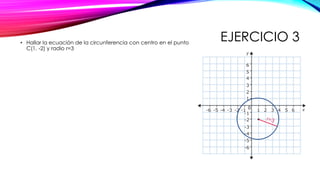
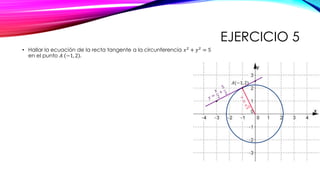
El documento explica cómo calcular la ecuación cartesiana de una circunferencia dados su centro y radio. Se define la distancia entre dos puntos y la fórmula para calcularla. Luego, se muestra cómo aplicar el Teorema de Pitágoras para derivar la ecuación cartesiana a partir de las coordenadas del centro y un punto de la circunferencia. Finalmente, se presenta la forma general de la ecuación cartesiana de una circunferencia y las condiciones que debe cumplir. Se incluyen varios ejercicios de aplicación.

1. LA CIRCUNFERENCIA
Ing. Gustavo Pincay Montalván

2. DISTANCIA ENTRE DOS
PUNTOS
• Dados dos puntos cualesquiera
A(x1,y1), B(x2,y2), definimos la
distancia entre ellos, d(A,B),
como la longitud del segmento
que los separa.
• Se puede calcular aplicando el
teorema de Pitágoras dado que
la distancia d es una medida de
un triángulo rectángulo

3. DISTANCIA ENTRE DOS
PUNTOS
• Ejemplo:

4. ECUACIÓN CARTESIANA DE LA
CIRCUNFERENCIA
• Teniendo una circunferencia de radio r
y un punto P(x, y) y centro C(0, 0)
• Determinamos la distancia de C a P, es
decir, su radio r
𝑑 = (𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2
• Donde C(0, 0)
• 𝑑 = (𝑥2 − 0)2 + (𝑦2 − 0)2
• 𝑟 = (𝑥2)2 + (𝑦2)2
• 𝑟2 = 𝑥2 + 𝑦2
Ecuación cartesiana o canónica de la
circunferrencia
P(x, y)

5. EJERCICIO 1
• Hallar la ecuación cartesiana de la circunferencia con centro en el eje de
coordenadas y P(3, 4) es un punto tangente de dicha circunferencia

6. EJERCICIO 2
• Hallar la ecuación cartesiana de la circunferencia con centro en el eje de
coordenadas y P(-5, -12) es un punto tangente de dicha circunferencia

7. ECUACIÓN CARTESIANA DE LA
CIRCUNFERENCIA
• Teniendo una circunferencia de radio r y centro C(h, k)
• Determinamos la distancia de C a cualquier punto P(x, y), es decir, su radio r
𝑑 = (𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2
• Reemplazamos valores: 𝑑 = (𝑥 − ℎ)2 + (𝑦 − 𝑘)2
• La distancia corresponde al radio de la circunferencia
𝑟 = (𝑥 − ℎ)2 + (𝑦 − 𝑘)2
• Despejando la raíz obtenemos la E. Cartesiana con centro en cualquier
lugar del plano cartesiano:
𝑟2 = (𝑥 − ℎ)2 + (𝑦 − 𝑘)2

8. C(-3, 4)
EJERCICIO 2
• Encontrar la ecuación y la gráfica de circunferencia de
centro C(-3, 4) y radio r=6.
• Determinar su ecuación canónica o cartesiana

9. ECUACIÓN GENERAL DE LA
CIRCUNFERENCIA
• Desarrollando la ecuación canónica o cartesiana de la circunferencia
obtenemos la ecuación de la forma 𝑥2 + 𝑦2 + 𝐷𝑥 + 𝐸𝑥 + 𝐹 = 0
(𝑥 − ℎ)2 + (𝑦 − 𝑘)2 = 𝑟2
𝑥2
− 2𝑥ℎ + ℎ2
+ 𝑦2
− 2𝑦𝑘 + 𝑘2
= 𝑟2
𝑥2
− 2𝑥ℎ + ℎ2
+ 𝑦2
− 2𝑦𝑘 + 𝑘2
− 𝑟2
= 0
• Ordenando temenos: 𝑥2
+ 𝑦2
− 2𝑥ℎ − 2𝑦𝑘 + ℎ2
+ 𝑘2
− 𝑟2
= 0
• Donde: 𝐷 = −2ℎ , 𝐸 = −2𝑘 , 𝐹 = ℎ2 + 𝑘2 − 𝑟2
• Entonces la podemos reescribir como:
Ecuación Genral de la Circunferencia 𝑥2
+ 𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0

10. CONDICIONES
Para que un polinomio de grado 2 en (x, y) represente una circunferencia
debe cumplir con las siguientes condiciones:
• Los coeficientes de 𝑥2
y de 𝑦2
sean iguales a la unidad. Si tuvieran un
coeficiente igual distinto de 1, podríamos dividir por este valor a todos los
términos de la ecuación.
• No tenga términos en 𝑥𝑦
•
𝐷
2
2
+
𝐸
2
2
− 𝐹 > 0

11. EJERCICIO 3
• Hallar la ecuación de la circunferencia con centro en el punto
C(1, -2) y radio r=3

12. EJERCICIO 4
• Indicar si la ecuación 4𝑥2
+ 4𝑦2
− 4𝑥 − 8𝑦 − 11 = 0, corresponde a
una circunferencia, de ser afirmativo, calcular el centro y el radio
y convertirla a la forma cartesiana.

13. EJERCICIO 5
• Hallar la ecuación de la recta tangente a la circunferencia 𝑥2
+ 𝑦2
= 5
en el punto 𝐴 −1, 2 .
𝐴(−1, 2)