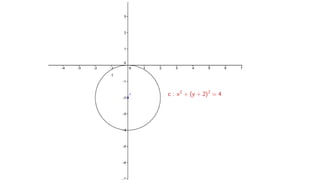
1. Se resuelven varios problemas relacionados con circunferencias, incluyendo hallar ecuaciones canónicas y generales dados centros y radios, determinar centros y radios a partir de ecuaciones, y encontrar longitudes y puntos tangentes. 2. Se explican los pasos para resolver cada problema, como encontrar el centro como punto medio de diámetros, usar la distancia entre puntos para hallar el radio, y sustituir valores en la fórmula canónica. 3. Los problemas cubren una variedad de casos como circunferencias tangentes a rectas,

1. DR. JAIME E. BRAVO H.
PRESENTA
PROBLEMAS
DE LA
CIRCUNFERENCIA
QUITO - ECUADOR

2. Los extremos de un diámetro de una circunferencia son
los puntos A(2,3) Y B(-4,5). Determina la ecuación y su
gráfica
1) Hallar el punto medio del diámetro A(2,3) Y B(-4,5) para
determinar el centro de la circunferencia.
X𝑴 =
𝑿𝑰+𝑿𝟐
𝟐
𝒀𝑴 =
𝒀𝟏+𝒀𝟐
𝟐
X𝑴 =
𝟐−𝟒
𝟐
= −𝟏 𝒀𝑴 =
𝟑+𝟖
𝟐
= 𝟒
𝑪 = (−𝟏; 𝟒)
2.-Calculamos la distancia del punto del centro ( -1,4) al
punto B para encontrar el valor del radio
𝒅 = 𝑿𝟐 − 𝑿𝟏 𝟐 + (𝒀𝟐 − 𝒀𝟏) 𝟐
𝒅 = √𝟒𝟎
𝒓 = √𝟏𝟎
3.- Ecuación canónica de la circunferencia
( X – h ) 2 + ( y – k ) 2 = r 2
( x + 1) 2 + ( y – 4 ) 2 = 10
Resolviendo la ecuación canónica se tiene
la ecuación general
X2 + 2x + 1 + y 2 – 8y + 16 – 10 =0
X 2 + y2 + 2x - 8y +7 =0

4. Una circunferencia tiene su centro en el punto
C(0,-2) y es tangente a la recta 5x-12y+2=0,
determine su ecuación
1.- Determinamos el valor del radio
con la siguiente fórmula:
𝒓 =
𝑨𝑿 + 𝑩𝒀 + 𝑪
𝑨 𝟐 + 𝑩 𝟐
𝒓 =
𝟓(𝟎) + (−𝟏𝟐)(−𝟐) + 𝟐
𝟓 𝟐 + (−𝟏𝟐) 𝟐
𝒓 =
𝟐𝟔
𝟏𝟑
𝒓 = 2
2.- Ecuación canónica de la
circunferencia
( X – h ) 2 + ( y – k ) 2 = r 2
( x - 0) 2 + ( y +2 ) 2 = 4
Resolviendo la ecuación
canónica se tiene la ecuación
general
X2 + y 2 + 4y + 4 – 4 =0
X 2 + y2 + 4y +7 =0

6. Determina la ecuación de la circunferencia de radio 5
y cuyo centro es el punto de intersección de las rectas
3x-2y-24=0, 2x+7y+9=0
1.- Resolvemos el sistema
de dos ecuaciones de dos
incógnitas para
determinar el valor de x e y
dicho punto constituye el
centro
Donde C ( 6 , - 3 )
2.- Ecuación canónica de la
circunferencia
( X – h ) 2 + ( y – k ) 2 = r 2
( x - 6) 2 + ( y +3 ) 2 = 25
Resolviendo la ecuación
canónica se tiene la ecuación
general
X 2 – 6x + y2 + 6y +20 =0

8. UNA CIRCUNFERENCIA TIENE SU CENTRO EN EL PUNTO C (6,2)
Y ES TANGENTE A LA RECTA 6X-8Y+10=0. DETERMINE SU
ECUACIÓN CANÓNICA Y GENERAL
1.- Determinamos el valor del radio
con la siguiente fórmula:
𝒓 =
𝑨𝑿 + 𝑩𝒀 + 𝑪
𝑨 𝟐 + 𝑩 𝟐
𝒓 =
𝟔(𝟔) + (−𝟖)(𝟐) + 𝟏𝟎
𝟔 𝟐 + (−𝟖) 𝟐
𝒓 =
𝟑𝟎
𝟏𝟎
𝒓 = 3
2.- Ecuación canónica de la
circunferencia
( X – h ) 2 + ( y – k ) 2 = r 2
( x - 6) 2 + ( y +2 ) 2 = 9
3.- Ecuación General de la
circunferencia
Resolviendo la ecuación canónica se
tiene la ecuación general
X2 + y 2 + 4y + 4 – 4 =0
X 2 + y2 -12 X + 4y +31 =0

9. 1.-RESOLVEMOS EL
SISTEMA DE
ECUACIONES
1) 4X-4Y+48=0
2)9X+6Y+18=0
X = - 6
Y = 6
Entonces el centro es
C ( - 6 ; 6 )
•DETERMINE LA ECUACION GENERAL DE LA
CIRCUNFERENCIA DE RADIO 4 Y CUYO CENTRO ES EL
PUNTO DE INTERSECCION DE LAS RECTAS 4X-4Y+48=0 ,
9X+6Y+18=0
2.- Ecuación canónica de la
circunferencia
( X – h ) 2 + ( y – k ) 2 = r 2
( x + 6) 2 + ( y -6 ) 2 = 16
3.- Ecuación General de la
circunferencia
Resolviendo la ecuación canónica se
tiene la ecuación general
X2 + y 2 + 4y + 4 – 4 =0
X 2 + y2 +12 X - 12y + 56 =0

10. Los extremos de un diámetro de una circunferencia son los puntos 𝐴 = 2,3 , 𝐵 = (−4,5) determina la
ecuación
1.- 𝑿 =
𝟐−𝟒
𝟐
𝒀 =
𝟑+𝟓
𝟐
𝑪 = −𝟏, 𝟒
𝟐. − (𝒙 + 𝟏) 𝟐
+ (𝒚 − 𝟒) 𝟐
= 𝒓 𝟐
(𝟐 + 𝟏) 𝟐
+(𝟑 − 𝟒) 𝟐
= 𝒓 𝟐
𝟗 + 𝟏 = 𝒓 𝟐
= 𝟏𝟎
3.- 𝒙 𝟐
+ 𝒚 𝟐
+ 𝟐𝒙 − 𝟖𝒚 + 𝟏𝟔 + 𝟏 = 𝟏𝟎
𝒙 𝟐
+ 𝒚 𝟐
+ 𝟐𝒙 − 𝟖𝒚 = −𝟕
1.Encontramos el punto medio
entre los dos puntos dados, ese
será el centro de la
circunferencia.
2.Reemplazamos en la formula
(𝑥 − ℎ)2+(𝑦 − 𝑘)2= 𝑟2 el centro y
luego cada uno de los puntos
para obtener el radio.
3. Sustituimos el radio en la
ecuación canónica y
encontramos la ecuación
general:

11. Dada la ecuación de la circunferencia 𝑥2 + 𝑦2 + 14𝑥 + 16𝑦 + 95 = 0
determine la ecuación canónica, el centro y el radio.
• 𝑥2 + 14𝑥 + 49 + 𝑦2 + 16𝑦 + 64 = −95
• (𝑥 + 7)2+(𝑦 + 8)2= 113 − 95
• 𝑅 = 3 2
• 𝐶 = (−7, −8)
1. Completamos el trinomio
de X y Y de la ecuación d
2. Encontramos la ecuación
formula 𝑥2
+ ℎ + 𝐶1 +
𝐶1 + 𝐶2
3. Hallamos el radio
4. El centro hallamos con la

12. RESUELVA LOS SIGUIENTES
PROBLEMAS
1.- DETERMINE LA
ECUACION DE LA
CIRCUNFERENCIA QUE
PASA POR EL
PUNTO(1,0) Y TIENE SU
CENTRO EN LA
INTERSECCION DE LAS
RECTAS 3X-2Y-24=0 Y
2X+7Y+9=0
2.- DADA LA ECUACION DE
LA CIRCUNFERENCIA
X2+Y2-12X-6Y-4=0
ENCONTRAR EL RADIO DE
LA CIRCUNFERENCIA
3.- Hallar la longitud de la
circunferencia cuya ecuación
es 𝟐𝟓𝒙 𝟐 + 𝟐𝟓𝒚 𝟐 + 𝟑𝟎𝒙 − 𝟐𝟎𝒚 − 𝟔𝟐 = 𝟎
4.- Una circunferencia es tangente a la
recta 𝟑𝒙 − 𝟒𝒚 + 𝟏 = 𝟎 , cuyo centro esta
en el punto 𝟑, 𝟐 . Hallar la ecuación de
la recta

13. 5.- Dada la ecuación de la
circunferencia
𝒙 𝟐
+ 𝒚 𝟐
+ 𝟏𝟒𝒙 + 𝟏𝟔𝒚 + 𝟗𝟓 = 𝟎
determine la ecuación
canónica, el centro y el radio.
6.- Encuentre la
ecuación general de la
circunferencia so el
centro es ( 3, 2 ) y el
radio es 7 cm
7.- Exprese en forma
general la ecuación
canónica
( X – 3 ) 2 + (y – 5 ) 2 = 20
8.- Hallar la ecuación de la
circunferencia que tiene de
centro ( 2,1) y pasa por el punto
( 3,4).
9.- Hallar la ecuación de la
circunferencia que pasa por los
puntos A ( 1, 2) B (6,5 ) y C ( 9,0 )
10.- Encuentre el centro y el
radio de la siguiente ecuación
X 2 + Y 2 - 20 X – 14 Y + 119 = 0