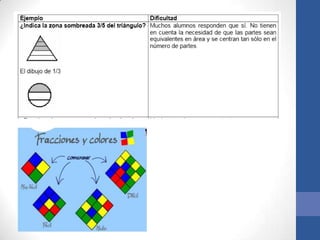
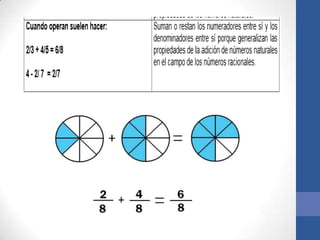
Este documento describe las dificultades que los estudiantes enfrentan al aprender fracciones, como la visualización del valor real de las fracciones y la comprensión de fracciones mayores a la unidad. También presenta estrategias para enseñar fracciones de manera efectiva, como usar lenguaje accesible para los estudiantes y actividades prácticas que desarrollen la comprensión de conceptos como áreas equivalentes y la relación entre el número de partes y el valor de cada parte. Los objetivos son que los estudiantes puedan identificar, escribir y compar

1. Escuela normal
superior del sur de
Tamaulipas
Especialidad: matemáticas
Nombre del normalista:
Mariano Martínez Loredo
Titular de la materia:
Ing. José Alejandro salinas Orta

2. LAS FRACCIONES Y SU ENSEÑANZA

3. • Las fracciones son un tema que requiere un cierto nivel
cognitivo que exige a los estudiantes a utilizar un pensamiento
abstracto de distintas formas. La problemática radica
principalmente en la dificultad de visualizar el valor real de las
fracciones.

4. • La matemática tiene por finalidad involucrar valores y
desarrollar actitudes en el alumno y se requiere el uso de
estrategias que permitan desarrollar las capacidades para
comprender, asociar, analizar e interpretar los conocimientos
adquiridos
para
enfrentar
su
entorno.

5. Principales dificultades
• La conceptualización de las fracciones lleva tiempo y los
alumnos lo necesitan para comprender, interpretar y usar sus
notaciones con sentido en las diferentes aplicaciones de las
mismas.
Estas dificultades tienen distintas índoles y que pueden provenir
desde falta de desarrollo cognitivo o simple por falta práctica

6. • La
comprensión
de
la
necesidad
de
áreas
(longitudes, volúmenes) de igual tamaño.
• La transición desde el diagrama a la expresión verbal y a su
simbolización.
• La comprensión de las fracciones mayores que la unidad.
• La identificación de una unidad en un diagrama que muestra
varias de ellas.

11. • De una y otra forma, se percibe que el alumno esta influido
por el uso que se les da a las fracciones en la vida diaria, es
por eso que en el ámbito escolar la palabra fracción forma
parte de un lenguaje relativamente familiar. el campo de
aplicación de cada fracción se va reduciendo
considerablemente, a excepción de un medio que es de uso
casi
universal

12. • Las fracciones deben ser acercadas al alumno mediante un
lenguaje que él entienda. Así surge la idea de
que, considerando los conocimientos que de las fracciones se
tengan, el inicio para un adecuado aprendizaje se puede hacer
partiendo de los términos más usuales.

13. • Piaget, Inheler y Szeminska (Dickson y otros;1991) puntualizan
siete criterios que denotarían tal comprensión:
• Considerar divisible una región entera (los niños pequeños se
niegan a cortar el entero)
• Admitir que el “todo” puede cortarse en cualquier número de
partes que se solicite.
• Comprender que las partes han de agotar el todo en la
división.
• Centrar la equivalencia de las partes en su tamaño.

14. • Distinguir entre número de cortes y número de partes (nº de
cortes y nº de partes no son necesariamente iguales)
• Comprender la relación inversa entre el número de partes
equivalentes y el valor de cada parte (a mayor nº de
partes, menor extensión de las mismas)
• Admitir la construcción del todo como suma de las partes, es
decir que el total se conserva aunque sea dividido en partes.

15. Consideraciones por parte del
profesor
Objetivos de la propuesta: Describen qué se espera que
aprendan los alumnos, que los niños logren
 Identificar fracciones equivalentes
 Escribir distintas representaciones de fracciones
 Comparar fracciones
 Resolver situaciones con números fraccionarios utilizando
distintas estrategias.

16. • Trabajar en grupo cooperando con respeto y paciencia para
resolver las situaciones.
• Confrontar resultados y justificarlos
• Sentir confianza en sí mismos y proponer ideas