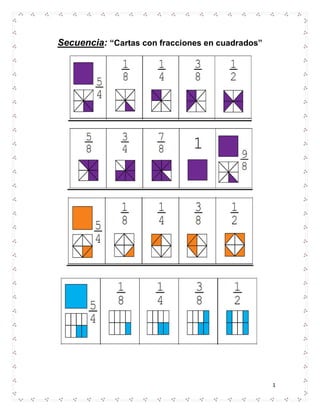
Cartas con fracciones en cuadrados
- 1. 1 Secuencia: “Cartas con fracciones en cuadrados”
- 2. 2
- 3. 3 MARCO DIDÁCTICO: Contenidos: 4to 5to 6to Interpretar la equivalencia entre expresiones fraccionarias de uso frecuente para una misma cantidad. Interpretar la equivalencia entre expresiones fraccionarias para una misma cantidad. (1 ) Comparar fracciones entre sí y con el entero a través de distintos procedimientos (relaciones numéricas, expresiones equivalentes, representaciones graficas). Argumentar sobre la equivalencia de distintas representaciones y descomposición de un número. Comparar fracciones a través de distintos procedimientos, incluyendo la representación en la recta numérica. La comprensión del sistema de números racionales pone en juego diversas nociones relacionadas, como fracciones, razones, decimales, así como una rica y compleja variedad de situaciones de uso y medios de expresión. Su estudio está condicionado por la progresiva comprensión de las operaciones aritméticas y de las situaciones de medición de magnitudes no discretas. Los números racionales son el primer conjunto de experiencias numéricas de los niños que no están basadas en los algoritmos de recuento como los números naturales. Hasta este momento el recuento en una forma u otra (hacia delante o hacia atrás, con saltos o no) se podía usar para resolver todos los problemas que se presentaban. Ahora con la introducción de los números racionales el algoritmodel recuento falla (o sea, no hay un número racional siguiente a otro dado; además, las fracciones se multiplican de manera diferente, etc.). La práctica y el discurso que se pone en juego con los "números racionales" suponen un salto importante en la manera de pensar y usar los números que origina dificultades a muchos alumnos. Las reglas de cálculo con las fracciones se pueden enseñar de manera simple: los alumnos pueden lograr una cierta destreza en el cálculo del denominador común para sumar o restar fracciones sencillas. De igual modo es posible que aprendan rápidamente las técnicas de multiplicar y dividir fracciones. Sin embargo, este
- 4. 4 enfoque algorítmico y memorístico tiene dos peligros: primero, ninguna de estas reglas ayuda a los estudiantes a pensar sobre el significado de las operaciones o por qué funcionan. Segundo, el dominio observado a corto plazo se pierde rápidamente. Las reglas de operación con las fracciones llegan a parecer similares y se confunden. El enfoque de la enseñanza de las fracciones debe ser el logro del sentido numérico y la resolución de problemas. En las orientaciones didácticas se indica: Los números fraccionarios se abordarán como partes de un grupo o de magnitudes continuas en diferentes contextos (reparto y medida). Mediante trabajos manipulativos se comienza con medios, cuartos.1 Posteriormente, trataremos el establecimiento de relaciones entre fracciones y el entero, entre decimales y el entero; entre fracciones y decimales entre sí, etc., ya que la consideración de estas relaciones y de las distintas escrituras posibles es parte fundamental de la construcción de este conocimiento. Este trabajo se inicia con la recuperación de ciertas relaciones que los niños y niñas ya pueden tener acerca de las fracciones o decimales más usuales: Un cuarto es la mitad de medio kilo, con 4 cuartos formo 1 kilo, con 2 monedas de 50 centavos completo $ 1, para escribir 25 centavos se puede usar un número con coma, como 0,25, para luego avanzar hacia su explicitación y generalización. En Cuadernos para el aula: Matemática 4, iniciamos la presentación de propuestas de trabajo con expresiones fraccionarias y decimales de los númerosracionales asociadas a contextos de uso social habitual que permitieron que los alumnos formularan relaciones y reglas de uso en esos contextos. En 5° año/ grado, habría que ampliar los contextos de uso, puesto que los alumnos ya estarían en condiciones de tomar como objeto de estudio las relaciones que establecen, por ejemplo, algunos criterios de comparación de números, para determinar cuándo funcionan y cuándo no. Más adelante, se avanzará en extender y generalizar esas relaciones y dar razones sobre su funcionamiento. En este sentido, “Formular leyes para comparar números, establecer la verdad o la falsedad de enunciados, analizar la equivalencia de expresiones numéricas sin apelar al cálculo efectivo, comparar diferentes procedimientos realizados por otros, delimitar el alcance de diferentes propiedades (esta regla vale en tales casos) son 1 Didáctica de las Matemáticaspara Maestros. Proyecto Edumat-Maestros.Eva Cid Juan D. Godino. Carmen Batanero. Página 223.
- 5. 5 tareas que, al ubicar al alumno en un plano de reflexión sobre el trabajo llevado a cabo, le permiten comprender aspectos de la organización teórica de la disciplina, le posibilitan acceder a las razones por las cuales algo funciona de una cierta manera. Lograr que los alumnos adquieran cierto nivel de fundamentación para los conceptos y propiedades con los que tratan, es un propósito de la educación matemática que la escuela tiene que brindar”2 Otro aspecto importante en el camino de avance en el reconocimiento y uso de estos números lo constituye la consideración del conjunto o familia con los cuales trabajar en este año/grado y con las nuevas relaciones que deseamos introducir. En este sentido, una propuesta podría ser la ampliación del repertorio de fracciones. Es el caso de la familia de los cuartos, los medios y los octavos hacia otras fracciones que continúen con la idea de seguir pensando en la “mitad de” (1/16, 1/32), incluyendo también los quintos, los décimos, los centésimos ylos milésimos; introduciendo el noveno, los doceavos y los dieciochoavos en la “familia” de los tercios; incluyendo fracciones mayores que la unidad, como 2 3/12, 7/2, 12/9 y otras relaciones, como “es 1/3 y medio”, “es 1/2 y 1/9”, etc. y todas las otras familias que se derivan del trabajo con comparaciones.3 En relación con las fracciones, en el año/grado anterior propusimos el trabajo con familias de fracciones como las siguientes: 1/2, 1/4, 1/8 (mitad, mitad de la mitad y mitad de la mitad de la mitad); 1/3, 1/6 (tercera parte y mitad de la tercera parte); 1/5, 1/10 (quinta parte y mitad de la quinta parte). En 5º año/grado proponemos continuar con estas, pero ampliando de la siguiente manera: 1/2, 1/4, 1/8, 1/16; 1/3, 1/6, 1/9; 1/5, 1/10, 1/100. Respecto de las relaciones entre las fracciones, trabajaremos la mitad, la tercera parte y la décima parte de cualquier fracción.4 A pesar de que la definición formal de número racional, los números racionales representan cantidades. Es por esto que la idea de que un número racional es una fracción no es del todo correcta, porque fracciones distintas puedenrepresentar el mismo número racional.5 El proceso de enseñanza-aprendizaje de las fracciones y de las operaciones con fracciones. 2 Extraído del documento Matemática. Fracciones y números decimales. Apuntes para la enseñanza (2005), Gobierno de la Ciudad de Buenos Aires, Secretaría de Educación, Dirección General de Planeamiento, Dirección de Currícula. 3 NAP. Cuadernos para el aula, matemática 5 - 1a ed. - Buenos Aires: Ministerio de Educación, Ciencia y Tecnología de la Nación, 2007. Páginas 48 y 49. 4 NAP. Cuadernos para el aula, matemática 5 - 1a ed. - Buenos Aires: Ministerio de Educación, Ciencia y Tecnología de la Nación, 2007. Página 50. 5 4. Números racionales. Página 107.
- 6. 6 Todos somos conscientes de las dificultades que presenta para los niños el aprendizaje de las fracciones, sobre todo en los niveles elementales. Estas dificultades, que abarcan tanto la comprensión conceptual como la destreza de cálculo, han sido constatadas por numerosos investigados de distintos países. Ello ha motivado la realización de estudios que tratan de detectar el origen de las dificultades para, a partir de su conocimiento, proponer soluciones, buscando aproximaciones alternativas para la enseñanza de las fracciones (SUYDAM, 1979). Según señala PAYNE(1976) en las investigaciones relativas a la enseñanza- aprendizaje de las fracciones realizadas en la década de los sesenta y setenta se pueden distinguir dos periodos: en un primer momento, el énfasis de los trabajos se centra en – comparar y analizar las ventajas e inconvenientes de los algoritmos de las operaciones con fracciones-. Para ello se estudiaban diferentes aproximaciones a la enseñanza de dichos algoritmos, que facilitan su comprensión –manejo a través de diagramas, materiales manipulativos, etc. En un segundo periodo el interés de las investigaciones se traslada a que es lo que los niños aprenden cuando las secuencias de enseñanza son desarrolladas minuciosamente. Por otra parte, GOUTARD (1964) ya atribuye las dificultades con las fracciones a la falta de experiencia con las mismas señalando que la diversidad de puntos de vista s esencial en su estudio a un nivel elemental, ya que su introducción de una forma única lleva a un conocimiento atrofiado. Según lo anterior, la autentica comprensión del concepto de fracción solo puede alcanzarse mediante representaciones plurales de dicho concepto. Esta es una de las razones que llevan a Goutard a defender las regletas Cuisinaire, como uno de los procedimientos a utilizar para la introducción de las fracciones. El método tradicional de introducir las fracciones era el representado por la relación parte todo, dividir un “todo” en partes y considerar algunas de ellas, lo que por otra parte parece ser la más intuitiva de las interpretaciones de la fracción. En la actualidad, parece ser una creencia bastante general la necesidad de proporcionar a los niños una adecuada experiencia con las muchas posibles interpretaciones de las fracciones si se quiere que lleguen a comprender el concepto. En particular es necesario incorporar ciertos aspectos y características de las fracciones que no han sido prácticamente considerados en la bibliografía hasta muy recientemente. Entre ellos se deben incluir los aspectos que potencian el papel de las fracciones como razón, como transformación, como cociente de
- 7. 7 números naturales en situaciones de reparto, su vinculación con los decimales, etc. Una opinión que creemos debe ser conocida es la representada por Freudenthal (1973). Según él “los niños pueden trabajar intuitivamente con fracciones intuitivas, siendo esta la razón por la que la introducción intuitiva que tradicionalmente se hace de las fracciones funcione excelentemente. La opinión de Freudenthal es dentro de la Aritmética solo debe explicarse aquella parte de las fracciones que sea accesible por los métodos intuitivos. El estudio de las fracciones debe continuarse después, dentro del Algebra.6 . 6 FRACCIONES: LA RELACION PARTE TODO. Salvador Linares. Victoria Sánchez. Páginas 30, 31 y 32.
- 8. 8 MARCO MATEMÁTICO: Números fraccionarios • Correspondencias entre fracciones sencillas y sus equivalentes decimales. • El tanto por ciento de una cantidad (%).7 Las variables didácticas de las situaciones de introducción de las fracciones son las siguientes: • Significado de las fracciones: parte- todo, comparación parte- parte, división de dos números, comparación de dos medidas, punto en la recta numérica, etc. • Tipos de fracciones: igual- distinto denominador, menores mayores que la unidad, enteras o no enteras, denominadores múltiplos unos de otros o no, etc. • Grado de contextualización de la situación: Situación que se refiere a materiales presentes en el aula y con el niño como actor. Situación hipotética contextualizada con material a disposición del niño para que pueda efectuar una representación simbólica. Situación hipotética contextualizada sin material a disposición del niño. • Tipo de material utilizado: Estructurado o no estructurado. • Posición de la incógnita en las operaciones: En el primer término, el término inicial o uno de los términos parciales. • Número de datos: Dos, tres o más. Modelos gráficos para el estudio de las fracciones Modelos de áreas Una figura, principalmente rectangular o circular se divide en partes iguales, sombreando la parte correspondiente a la fracción representada. 7 DIDÁCTICA DE LOS SISTEMAS NUMÉRICOS PARA MAESTROS Capítulo 4: FRACCIONES Y NÚMEROS RACIONALES POSITIVOS. E. Cid, J. D. Godino y C. Batanero. Página 224.
- 9. 9 ¿Qué fracción expresa la relación entre el área de la superficie sombreada y la superficie del rectángulo mayor? ¿Cuánto mide el área sombreada si usamos como unidad de medida el rectángulo mayor? Representación mediante conjuntos Cuando el conjunto que se quiere dividir es discreto y el número de objetos es múltiplo de las partes, una representación de los objetos puede visualizar el problema de reparto. Modelos lineales Al igual que en el caso de los números naturales, podemos visualizar las fracciones a lo largo de una recta. Tomamos en ella una cierta longitud como unidad a repartir, y a partir de ella representamos la fracción. 8 Notación usual: 1. En este caso, una fracción se representa por números que estánescritos uno sobre otro y que se hallan separados por una línea recta horizontal llamadaraya fraccionaria. La fracción está formada por dos términos: el numerador y eldenominador. El numerador es el número que está sobre la raya fraccionaria y eldenominador es el que está bajo la raya fraccionaria. 2. Decimal: 0.5. 3. Porcentaje: 50%. 4. Sistema sexagesimal (Horario) 12:15:30. 5. Equivalencia: = . 6. Número mixto: =1+ . 8 DIDÁCTICA DE LOS SISTEMAS NUMÉRICOS PARA MAESTROS Capítulo 4: FRACCIONES Y NÚMEROS RACIONALES POSITIVOS. E. Cid, J. D. Godino y C. Batanero. Páginas 231 y 232.
- 10. 10 _Para comparar fracciones y decir si una es mayor que otra o si son iguales, se puede recurrir a la recta numérica: Fracciones: Adición Para resolver una adición de dos o más fracciones con igual denominador se suman los numeradores y se conserva el denominador. + = Sustracción Para resolver una sustracción de dos fracciones con igual denominador se restan los numeradores y se conserva el denominador. - = Para sumar o restar fracciones con distinto denominador puedes: Amplificar o simplificar todas o algunas de las fracciones dadas para obtener fracciones con denominadores iguales. Sumar o restar los numeradores según corresponda y conservar el denominador. Simplificar para expresar el resultado como fracción irreductible.9 Producto 9 Resignificación del algoritmo para operar aditivamente con fracciones en un contexto escolar.
- 11. 11 La justificación matemática del algoritmo convencional para multiplicar dos fracciones Se explica en el desarrollo de los fundamentos matemáticos centrales. Cociente La justificación matemática del algoritmo convencional para dividir dos fracciones Se explica en el desarrollo de los fundamentos matemáticos centrales. Principios y exigencia, dificultades del cálculo mental. Cálculo mental: conjunto de procedimientos que, analizando los datos por tratar, se articulan sin recurrir a un algoritmo preestablecido para obtener resultados exactos o aproximados. El cálculo mental frecuentemente se asocia a la idea de una resolución oral y rápida. El tipo de cálculo que propone el Diseño Curricular no implica necesariamente “no escribir”. Propone un trabajo que apunta, desde los primeros años de la Escuela Primaria, a que los alumnos aprendan a usar variadasestrategias para resolver cálculos mentales, a seleccionar la más conveniente de acuerdo con la situación y con los númerosinvolucrados, a verificar con una estrategia los resultados obtenidos por medio de otra, entre otros contenidos matemáticos. Dificultad: Sin embargo, si se enseña a “agregar ceros” como una regla desvinculada del valor posicional, los niños pueden no encontrar el sentido de esta técnica. En tal caso, algunos podrían extender erróneamente esta regla para el caso en que se agreguen cifras que no sean ceros, como por ejemplo, si 8 + 3 = 11 entonces 81 + 31 = 111 ó 82 + 32 = 112. Una regla que solo ha sido enunciada, para la que no se ha tenido la oportunidad de establecer las razones por las cuales es válida hace que no se pueda determinar su campo de validez. ¿Por qué solo sirve cuando se agregan ceros? El mero enunciado no lo responde. Las técnicas de cálculo que se utilizan dependen de los números que intervienen y de las relaciones que los alumnos hayan podido establecer entre esos números.
- 12. 12 Desde sus primeros contactos con los números, los niños pueden hacer cálculos “en la cabeza”. Por ejemplo, si se les propone resolver el cálculo 5 + 6, algunos pueden hacer uso de sus dedos contando a partir de 5 o de 6, o de lápices utilizando el conteo para obtener 11. Otros pueden “guardar” el 6 en la cabeza y contar 5 más a partir de él: 7, 8, 9, 10 y 11, es decir usan el sobre conteo desde 6. ERRORES EN LAS FRACCIONES Una gran parte de los errores que los niños cometen al trabajar con fracciones tiene su origen en la similaridad que, tanto en el lenguaje como en la simbología, presentan con los números naturales. Por un lado, las fracciones se nombran utilizando nombres iguales o muy parecidos a los que ya le son familiares en el contexto de los números ordinales; así por ejemplo se dice “un cuarto”, “dos quintos”, etc. Por otro lado y eso es lo más grave, los símbolos de los números naturales se utilizan también para las fracciones añadiendo simplemente una rayita horizontal. El niño tiene experiencia con los números naturales y esto conlleva una tendencia a ver las fracciones como un conjunto de dos números naturales separados por una rayita. La consecuencia es que trata de utilizar sus conocimientos de cálculo con los números naturales, para lo cual extrapola a las fracciones las reglas y algoritmos de aquellos. Esto constituye lo que algunos autores han denominado “efecto de distracción de los números naturales”. La influencia que el conocimiento de los números naturales ejerce en el proceso de aprendizaje de las fracciones se manifiesta en muchos otros aspectos. Es difícil para el niño entender que el producto de dos fracciones puede ser menor que ellas, al contrario de lo que sucede con dos números naturales. Como lo que él tiene asimilado son los algoritmos con esos números a menudo trata de forzar los algoritmos con fracciones de manera que el resultado se ajuste a lo que le dicte su intuición. En resumen el paso de los números naturales a los fraccionarios no es fácil para los niños. Presenta dificultades tanto conceptuales como algorítmicas. El profesor debe estar pendiente de la evolución de los errores de los niños y huir de la tentación de creer que con la simple practica repetitiva se irán subsanando. Algunos ejemplos típicos de errores con fracciones: Errores en la noción de equivalencia de fracciones Ejemplo 1. A veces nos encontramos con la siguiente respuesta ante una tarea de búsqueda de fracciones equivalentes.
- 13. 13 = = Aquí se refleja una situación en la que la fracción se considera como un par de números naturales que no están relacionados entra sí. La respuesta esta basada en el reconocimiento de un modelo aditivo en los numeradores (sumar seis) que se traslada a los denominadores. Algunas investigaciones han mostrado también que los niños presentan problemas ante la transitividad del signo igual. Así Hart (1981) señala que ante una expresión del tipo: = = Los alumnos tienen mayor dificultad encalcular, ya que una vez calculado el valor 8 para el numerador de la segunda fracción comparan 8/12 con 14/, lo que resulta más difícil que hacerlo con 2/3. El no utilizar 2/3 = 14/ puede ser debido a que solo se fijan en la igualdad de las dos últimas fracciones. Estos resultados deben ser tenidos en cuenta al plantear nuestras actividades. La visualización puede jugar aquí también un importante papel. Ejemplo 2.un niño que se le pide que simplifique una serie de fracciones escribe las siguientes respuestas: = = = = = A primera vista parece no existe ninguna lógica en estos resultados.Sin embargo un análisis más detallado muestra que el niño ha elaborado una regla que para simplificar fracciones asocia a cada numero natural otro más sencillo por el cual se sustituye. En concreto dos pasa a ser uno, tres también uno, cuatro es dos, seis es tres, y nueve es tres. Seguramente ha extrapolado este procedimiento de los ejemplos que ha visto hacer al profesor. Obsérvese además que su regla le da un resultado correcto en bastantes casos. Lo primero que hay que hacer antes de iniciar la corrección es determinar si el niño tiene clara la noción de fracción. Si no la tuviera, es claro que la enseñanza deberá recomenzar desde ahí. Errores en la adición de fracciones: Consideremos ahora las respuestas
- 14. 14 + = + = + = + = Estas respuestas corresponden a uno de los errores más comunes a la adición de fracciones que consiste en que el niño suma independientemente los numeradores y denominadores. Usos que realizamos con los números racionales positivos a. La fracción como expresión que vincula la parte con el todo (continuo o discontinuo).responde a la pregunta la pregunta ¿qué parte es? del entero en cuestión. b. La fracción como reparto equitativo. Responde a la pregunta ¿cuánto le corresponde a cada uno? c. . La fracción como razón. Sirve a la pregunta ¿en qué relación están? d. La fracción como división indicada. e. La fracción como un punto de la recta numérica. f. La fracción como operador.10 10 La enseñanza de las fracciones en el 2do ciclo de la Educación General Básica. Módulo 2. Serie Aportes al Proyecto Curricular Institucional Agosto 2001. Página 7 y 8.
- 15. 15 Eje:Números yOperaciones Año:5to Ciclo: 2º Contenido del diseño: _Elaboración de recursos de cálculo mental basándose en descomposiciones aditivas que den 1 . _Comparación y orden de fracciones. _Ubicación de fracciones entre números naturales y entre otras fracciones en la recta numérica. _Elaboración y utilización de distintos procedimientos para resolver problemas que involucren sumas de fracciones para llegar a 1 ½. Contenidos procedimentales: _Construir un conjunto equivalente a un entero y medio (1 y ½), con fracciones de valor 1,1/8,1/4, 3/8,1/2,5/8,3/4,7/8,9/8,5/4. _Resolución mental de adiciones simples de fracciones (ej. 1/2 +1 /4; 1...;) Contenido Actitudinales: _Seguridad en la defensa de sus argumentos y flexibilidad para modificarlos. _Valoración del trabajo cooperativo y la toma de responsabilidades para lograr un objetivo común. _Reflexión crítica sobre los productos obtenidos y las estrategias utilizadas. Objetivos: Que lo alumnos: _Relacionen entre fracciones diferentes (medios, tercios). _Relacionen fracciones equivalentes. _Comparen entre fracciones, según sus diferentes denominadores.
- 16. 16 Conocimientos previos: _Familia de fracciones. _Equivalencia de fracciones. _Descomposición aditiva de fracciones Tiempo: 80 minutos. Tema: Cartas con fracciones en cuadrados “Uno y medio” Reglas del juego: _Se juegan 4 rondas. En cada ronda, uno de los jugadores reparte y no se da cartas a sí mismo (es el “cartero”). _Se mezclan las cartas y el cartero reparte una a cada jugador, quienes la ubican boca abajo, cada jugador levanta y mira su carta –sin mostrarla– y en la siguiente ronda, a su turno, le dice al cartero que quiere una carta más –tantas veces como desee, hasta que decida “plantarse”– o que no quiere más cartas. _Se trata de acercarse a 1 1/2 tanto como se pueda. Para decidir quién gana cada ronda, una vez que los tres jugadores declararon que no quieren más cartas, cada uno/a calcula cuánto tiene (la suma de sus cartas) y pone su ficha sobre el número correspondiente a la suma de sus cartas en la “recta numérica”, con lo cual es prácticamente inmediata la comparación de las fracciones resultado. Se muestran las cartas y controlan entre todos, si alguien no está de acuerdo con el resultado, tiene que explicar por qué. _Cuando todos acuerdan quién es el ganador, se anota el puntaje de la ronda. En cada ronda se juega un punto. • El que se pasa de 1 1/2, no recibe puntos en esa ronda. • Si un solo jugador sumó exactamente 1 ½, gana el punto de esa ronda. • Si nadie sumó 1 1/2, gana el punto quien más se aproximó. • Si hay empate, se fracciona el punto en partes iguales (medios o tercios). Se puede jugar cuatro u ocho rondas en cada partido, para que cada uno tenga la oportunidad de ser “cartero”. Organización de la clase: Se jugaran en grupo de cuatro integrantes, los cuales estarán sentados con las mesas enfrentadas para que puedan jugar mejor y puedan confrontar sus opiniones.En la segunda implementación de esta secuencia se cambiaron los grupos para evitar que la clase se desarme por la actitud de algunos alumnos.
- 17. 17 Materiales: _El mazo de cartas de fracciones (son 40 cartas en 4 “palos”, con los valores: 1,1/8,1/4,3/8,1/2,5/8,3/4,7/8,9/8,5/4). _Una hoja en blanco y un lápiz para anotar por alumno. _Una tira de cartulina donde se ha representado la recta numérica con una marca 11/2. Posibles procedimientos de los alumnos para llegar a formar el 1 1+1/2 + 1+1/4+1/4 + + 1+1/8+1/8+1/4 + + + 5/4+1/8+1/8 + + 3/8+1/8+1
- 18. 18 + + ½+1/2+ ¼+1/4 + + + 9/8+1/8+1/4 + + 3/8+1/8+1/2+1/2 + + + 7/8+1/8+1/4+1/4 + + + 7/8+1/8+1/2 + + 5/8+3/8+1/2 + + 5/8+3/8+1/4+1/4
- 19. 19 + + + 7/8+3/8+1/4 + + 7/8+3/8+1/8+1/8 + + + Jugadas que pasan al total de la fracción en juego: 9/8+5/8 = 1 3/4 + 5/8+1/4+3/4= 1 5/8 + + 7/8+1/2= 1 3/8 + 9/8+5/4=2 2/8 + 1/4+3/8+5/4=1 7/8
- 20. 20 + + Jugadas que no llegan al “Uno y medio” 1/8+1+1/4= 1 3/8 + + 3/4+1/4+1/4 = 1 ¼ + + 9/8= 1 1/8 5/8+1/8+1/2= 1 2/8 + + Puesta en común: Una vez que todos los grupos hayan terminado de jugar las cuatro rondas en la clase y analizando los procedimientos que cada grupo utilizo para llegar al 1 ½,en el pizarrón (pasara a escribir la producción el que más se aproximo, pero se le preguntara a otro integrante del grupo o al total de la clase para ver si se apropiaron de las reglas del juego y para ver si todos entendieron) se procederá a dar el cierre de la clase.
- 21. 21 A partir de la intervenciones que se realizaran retomando los conceptos trabajados anteriormente en clase,(suma de fracciones, equivalencia de fracciones). Cuentas que ya sabemos: ) + =1 ) + + + =1 ) + + + + + + + =1 + + + =1 + + + + = + = =1entero Cuando tenemos una fracción con igual numerador y denominador formamos 1 entero. Vero 1+ Lorena + Antonela Gane porque es el que se aproxima más a 1 ½. Posible intervención docente:
- 22. 22 ¿Por qué creen que vero gano? ¿Cuánto le falta a Lorena para llegar al uno y un medio? En las cuentas que ya sabemos¿Cuántos cuartos forman un entero? En la escritura de Antonela ¿que ven de distinto? ¿Les pareció vio en otro lugar esa escritura? ¿En qué lugares? ¿Es lo mismo escribir que 1 ? ¿Valen lo mismo? Análisis: + + + + = + = 1 entero + por eso decimos que y son equivalentes ; 1/2Diferentes formas de escribir fracciones. En la carpeta: 17/06/15 Matemática Cartas con fracciones en cuadrados “1 ”. Equivalencia de fracciones: + + + + = + =
- 23. 23 1 entero + por eso decimos que y son equivalentes. Otra forma de escribir las fracciones: ; 1/2 Podemos verlas en la PC y en los supermercados. Institucionalización: Cuando el numerador es mayor que el denominador la fracción va a ser mayor que el entero. Para comparar dos fracciones de igual numerador, se compara el denominador. El que tiene menor denominador es el mayor. Para comparar dos fracciones de igual denominadores, se compara los denominadores. El que tiene mayor numerador es el menor. Prolongación: (partidas simuladas) Actividad: a) Jugando a cartas con fracciones en cuadrados, Martin tiene dos cartas una de y la otra de . ¿con que cartas puede formar el 1 ? b) María tiene dos cartas una de y la otra de . Si en la mesa hay dos cartas de , tres de y cuatro de . ¿Qué cartas puede levantar para formar 1 ? c) Completa las siguientes sumas: a)1+_+ = b) + + _+ + =
- 24. 24 c)_+ + = ) +_+ = ) + +_= Posible intervención docente: ¿Con que cartas puedo llegar al 1 ? A ¿cuántos cuartos le falta para llegar al entero? Si levanto tres cartas de ¿cuánto obtengo? ¿Cuánto me falta para llegar al 1 ? Si tengo 1 y ¿Cuánto me falta para completar y llegar al 1 ? En las cuentas que ya sabemos + ¿Cuánto es? ¿Cuánto me falta para llegar al 1 ?