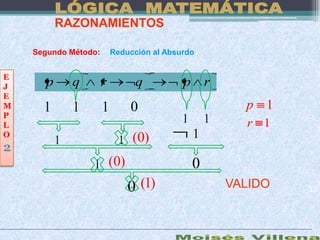
Este documento presenta los conceptos básicos de la lógica proposicional. Define proposiciones, operadores lógicos como la negación, conjunción, disyunción y condicional. Explica las tablas de verdad y cómo determinar el valor de verdad de proposiciones compuestas. También introduce conceptos como tautologías, contradicciones, implicaciones lógicas y equivalencias lógicas.

1. 1

2. 2
PROPOSICION
Enunciado al que se lo puede calificar o
bien como Verdadero o bien como Falso.
NOTACIÓN:
Primeras letras del abecedario en minúscula
Ejemplos:
a: "Hoy es Lunes"
b: "Estoy en la clase de Física"

3. 3
• NO PROPOSICIONES
 ¡Ojala deje de llover!
 ¿Hiciste el deber de Matemáticas?
 Siéntate y quédate quieto.
VALOR DE VERDAD
Cualidad de una proposición de ser verdadera o
de ser falsa.
Verdadero: 1
Falso: 0

4. 4
OPERADORES (CONECTORES) LÓGICOS
NEGACIÓN Lenguaje No
No es verdad que
Relacionado
No es cierto que
Símbolo : 
Tabla de verdad
Ejemplos
a a
a : "Hoy no es Lunes "
b :“ No Estoy en la clase de Física" 1 0
0 1

5. 5
OPERADORES LÓGICOS
CONJUNCIÓN
Lenguaje
Relacionado “y” “pero”
Símbolo:
Ejemplo Tabla de verdad
a : "Tengo un lápiz" a b a b
b : "Tengo un cuaderno" 1 1 1
1 0 0
a b : "Tengo un lápiz y un cuaderno " 0 1 0
0 0 0

6. OPERADORES LÓGICOS
DISYUNCION INCLUSIVA
Lenguaje
“O”
Relacionado
Símbolo:
Ejemplo
Tabla de verdad
a : "Tengo un lápiz"
a b a b
b : "Tengo un cuaderno " 1 1 1
a b : "Tengo un lápiz o un cuaderno " 1 0 1
0 1 1
0 0 0
6

7. OPERADORES LÓGICOS
DISYUNCION EXCLUSIVA
a
Lenguaje “0……o.…..”
b
Relacionado “o bien……o bien…..”
a b
Símbolo: Significa: a b a b
Ejemplo Tabla de verdad
a b a b
a : “Daniel está en España "
1 1 0
b : “Daniel está en Italia"
1 0 1
a b : “Daniel está en España o en Italia" 0 1 1
0 0 0
7

8. OPERADORES LÓGICOS
ENUNCIACIÓN HIPOTÉTICA (CONDICIONAL)
Lenguaje a
“Si…..entonces.….”
b
Relacionado
Ejemplo Símbolo: a b
a : “Apruebas el preuniversitario"
b : “Te regalaré un carro"
a b : “Si apruebas el preuniversitario entonces te regalaré un carro"
Tabla de verdad a b a b
1 1 1
1 0 0
0 1 1
0 0 1
8

9. OPERADORES LÓGICOS
ENUNCIACIÓN HIPOTÉTICA (CONDICIONAL)
a b
Antecedente Consecuente
Hipótesis Tesis
Premisa Conclusión.
OTROS LENGUAJES RELACIONADOS:
a implica b b cada vez que a
Basta a para b b siempre que a
a sólo si b b puesto que a
a solamente si b b porque a
b si a b con la condición de que a9

10. OPERADORES LÓGICOS
ENUNCIACIÓN HIPOTÉTICA (CONDICIONAL)
Condición Necesaria y
Condición Suficiente verdadera a b
“a es condición suficiente para b”
“b es condición necesaria para a”
Ejemplo:
"Si un número es divisible para 4 entonces es divisible para 2"
1. “La divisibilidad para 4 es condición suficiente para la divisibilidad para 2"
“Es suficiente que un número sea divisible para 4 para que se divisible para 2"
2. “La divisibilidad para 2 es condición necesaria para la divisibilidad para 4"
“Es necesario que un número sea divisible para 2 para que se divisible para 4"
10

11. OPERADORES LÓGICOS
ENUNCIACIÓN HIPOTÉTICA (CONDICIONAL)
VARIACIONES a b
LA RECÍPROCA: b a
LA INVERSA: a b
LA CONTRARRECÍPROCA: b a
Ejemplo: “Iré a trabajar si me pagan”
Si me pagan entonces iré a trabajar
LA RECÍPROCA: Si voy a trabajar entonces me pagan
LA INVERSA: Si no me pagan entonces no iré a trabajar
LA CONTRARRECÍPROCA: Si no voy a trabajar entonces no me pagan
11

12. OPERADORES LÓGICOS
ENUNCIACIÓN HIPOTÉTICA (CONDICIONAL)
VARIACIONES a b
Importante
Condicional:
"Si un número es divisible para 4 entonces es divisible para 2"
RECÍPROCA:
"Si un número es divisible para 2 entonces es divisible para 4"
Falso
Contraejemplo:
“6 es divisible para 2, pero no es divisible para 4"
12

13. BICONDICIONAL OPERADORES LÓGICOS
Lenguaje Relacionado “…..si y sólo si.….”
a b
Símbolo: a b Significa: a b b a
TABLA a b a b
DE 0 0 1
VERDAD 0 1 0
1 0 0
Ejemplo: 1 1 1
a : “Un triángulo es equilátero”
b : “Un triángulo tiene sus ángulo de igual medida”
a b : “Un triángulo es equilátero si y sólo si tiene sus ángulos de
igual medida”
13

14. PROPOSICIONES SIMPLES Y COMPUESTAS
Simples: No poseen operador lógico
Compuestas: Formadas por varias proposiciones
y operadores lógicos
El valor de verdad de
Ejemplo: a b c a b una proposición
compuesta depende del
Suponga que: a 1 b 0 c 1 valor de verdad de sus
proposiciones simples.
1 0 1 1 0
1 0 1 1 0

  
10 1 1 0 0

1 
 0
0
 
1
 
0
 
0
 
1
14

15. PROPOSICIONES SIMPLES Y COMPUESTAS
Ejemplo:
Determine el valor de verdad de las proposiciones
simples sabiendo que el valor de verdad de la
proposición compuesta es VERDADERO.
a b c d a c d
1 1 0 1 1 1
1
0 0 a 1
c 0
1
1 d 1
b 0
1
15

16. FORMAS PROPOSICIONALES
Expresión constituida por símbolos que
representan o conectores lógicos o variables
proposicionales.
Ejemplo p q r p q Total = 2núm. var. prop.
p q r p q r p q r p q p q r p q
1 1 1 1 0 0 1 1
1 1 0 1 1 1 1 1
1 0 1 1 0 0 0 1
1 0 0 1 1 1 0 0
0 1 1 1 0 0 0 1
0 1 0 1 1 1 0 0
0 0 1 0 0 0 0 1
0 0 0 0 1 0 0 1
16

17. FORMAS PROPOSICIONALES
TAUTOLOGÍA
Si se obtienen sólo proposiciones verdaderas para todos los valores
de verdad de las variables proposicionales
Ejemplo
p q p q
p q p q p p q p q p q
1 1 1 0 1 1
1 0 0 0 0 1
0 1 1 1 1 1
0 0 1 1 1 1
CONTRADICCION: Si se obtienen sólo proposiciones falsas
CONTINGENCIA: Si se obtienen proposiciones verdaderas y
otras falsas.
17

18. IMPLICACIONES LÓGICAS
Sean A y B dos formas proposicionales, se
dice que A implica lógicamente a B si y sólo
si A B es una tautología.
En este caso se escribe: A B
Ejemplo
p q p q
18

19. IMPLICACIONES LÓGICAS
Algunas implicaciones lógicas típicas son:
p p q Adición
p q p Simplificación
p p q q Modus Ponens
p q q p Modus Tollens
p q p q Silogismo Disyuntivo
p q q r p r Silogismo Hipotético
19

20. EQUIVALENCIAS LÓGICAS
Sean A y B dos formas proposicionales. Se dice
que A es lógicamente equivalente a B si y sólo si
A B es una tautología.
En este caso se escribe: A B
También: A B
Ejemplo p q p q
p q p q p p q p q p q
1 1 1 0 1 1
1 0 0 0 0 1
0 1 1 1 1 1
0 0 1 1 1 1
20

21. ALGEBRA DE PROPOSICIONES
CONJUNCIÓN DISYUNCIÓN
p q q p Conmutativa p q q p
p q r p q r Asociativa p q r p q r
p p p Idempotencia p p p
p 1 p Identidad p 0 p
p 0 0 Absorción p 1 1
21

22. ALGEBRA DE PROPOSICIONES
Otras:
p q r p q p r
Leyes distributivas
p q r p q p r
p p Doble negación
p q p q
Leyes de De Morgan
p q p q
p q q p Contrarrecíproca
p q p q Implicación
22

23. ALGEBRA DE PROPOSICIONES
Otras:
p p 1 Ley del tercer excluido
p p 0 Ley de la contradicción
p q r p q r Ley de exportación
p q p q 0 Reducción al absurdo
23

24. E
J Demostrar: p p q p
E
M
P
Solución:
L
O
p p q p 0 p q Identidad
p q q p q Contradicción
p q p q p q Distributivas
p q p q Idempotencia
p q q Distributivas
p 0 Contradicción
p Identidad
24

25. Sea la proposición:
E
J “Si tú eres inteligente y no resuelves el problema
E entonces desconoces la materia ”
M Siendo:
P m: Tú eres inteligente
L n: Tú resuelves el problema
O p: Tú desconoces la materia
Indique a que opción corresponde la TRADUCCIÓN:
a) m n p Solución:
b) p m n
Primero: Traducción: m n p
c) m n p
d) m p n Segundo: Transformamos empleando el álgebra de
proposiciones:
e) m n p
m n p Implicación
m n p Ley de De Morgan
m n p Asociativa de la disyunción
m n p Implicación
25

26. Sea la proposición:
E
J “Hoy es jueves y tengo que dar un examen, pero si
E hay huelga, entonces no voy a la Universidad”
M Siendo: a: Hoy es jueves
P b: Tengo que dar un examen
L c: Hay huelga
O d: Me voy a la Universidad
Indique a que opción corresponde la TRADUCCIÓN:
a) a b c d Solución:
b) a b c d
Primero: Traducción: a b c d
c) d c a b
d) a b c d Segundo: Transformamos :
e) c d a b a b d c Contrarrecíproca
a b d c Doble Negación
d c a b Conmutativa
26

27. RAZONAMIENTOS
PREMISAS O HIPOTESIS
 
   

CONCLUSIÓN
H1 H 2 H 3  H n C

 
OPERADOR PRINCIPAL
VALIDEZ
Un razonamiento es VÁLIDO cuando la forma
proposicional que se obtiene de la proposición
compuesta que lo define, es tautológica.
27

28. 28
RAZONAMIENTOS
E
J "Si aumenta la producción, aumentan los ingresos; si
E aumentan los ingresos, se recupera la inversión. Por lo
M
P tanto, si aumenta la producción ,se recupera la inversión"
L
SOLUCIÓN:
O a: Aumenta la producción
1 b: Aumentan los ingresos
c: Se recupera la inversión
Traducción:
a b b c a c
Forma proposicional:
p q q r p r

29. 29
RAZONAMIENTOS
E
J p q q r p r
E
M PRIMER MÉTODO: Aplicando leyes de Equivalencias
P
L p q q r p r Implicación
O
p q q r p r De Morgan
1
p q q r p r De Morgan
p q p q r r Asociativa
p p q p q r r r Distributiva
1 q p q r 1 Del Tercero excluido
q p q r Identidad para la conjunción
q q p r Asociativa
1 p r Del Tercero excluido
1 Absorción para la disyunción

30. 30
RAZONAMIENTOS
E
J
E
Segundo Método: Reducción al Absurdo
M
P
L
O p q q r p r
1
1 1 1 0
1 1 (0) 1 0 p 1
0 r 0
1 (0)
0 (1) VALIDO

31. RAZONAMIENTOS
E
J "Si soy estudioso , aprobaré el curso ; si soy fiestero, no
E aprobaré el curso. Por lo tanto, no puedo ser estudioso
M
P y fiestero al mismo tiempo"
L Solución: a: Soy estudioso
O
b: Aprobaré el curso
2 c: Soy fiestero
Traducción:
a b c b a c
Forma proposicional:
p q r q p r
31

32. RAZONAMIENTOS
PRIMER MÉTODO: Aplicando leyes de Equivalencias
p q r q p r Implicación
p q r q p r De Morgan
E
J p q r q p r De Morgan
E
M p q r q p r Doble negación
P
L p q p r q r Asociativa
O
p p q p r r q r Distributiva
2
1 q p 1 q r Del tercero excluido
q p q r Identidad para la conjunción
Asociativa
q q p r
1 p r Del tercero excluido
1 Absorción para la disyunción
32

33. RAZONAMIENTOS
Segundo Método: Reducción al Absurdo
E
J p q r q p r
E
M 1 1 1 0 p 1
P
L
1 1 r 1
O
1 1 (0) 1
2
1 (0) 0
0 (1) VALIDO 33

34. 34
E RAZONAMIENTOS
J
E
La Lógica es difícil o no les gusta a muchos
M estudiantes. Si la Matemática es fácil, entonces la
P Lógica no es difícil. Por lo tanto, la Lógica es difícil.
L
O Solución: a: La lógica es difícil
3 b: La lógica les gusta a muchos estudiantes
c: La Matemática es fácil. a b c a a
p q r p p
0 0 p 0

0 1 
1 1 q 0
 
1 1 r 1 r 0
 1 0
NO VALIDO
0