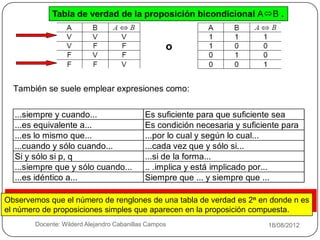
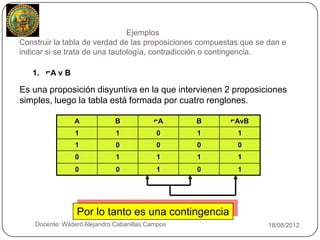
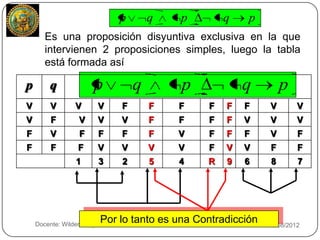
El documento resume los conceptos básicos de las tablas de verdad, tautologías, contradicciones y conectivos lógicos como la negación, disyunción inclusiva, disyunción exclusiva, conjunción, condicional y bicondicional. Explica cómo construir tablas de verdad para proposiciones compuestas y determinar si son tautologías, contradicciones o contingencias. También presenta ejemplos de tablas de verdad y esquemas moleculares.

2. Tablas de verdad, Tautologías y Contradicciones
A toda proposición “A” se le asocia un valor de verdad,
siendo este verdadera o falsa, lo cual se representa
como:
Valor de verdad de A = V(A) = V = verdadero
Valor de verdad de A = V(A) = F = falso
también se acostumbre representarlo por:
V(A) = 1 = verdadero o V(A) = 0 = falso
Es importante considerar que en la proposición condicional
A B , la A es el antecedente y B es el consecuente.
2 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

3. Tabla de verdad de la proposición negativa ⌐A.
o
La negación, puede traducirse como:
No es cierto que ... Nadie que sea ... Jamás...
Es falso que... No es el caso que ... Es inconcebible que...
Nunca ... No es verdad que Es imposible que...
No ocurre que... Es absurdo que Es erróneo que ...
Es mentira que ... No acaece que... De ningún modo ...
No es el caso que... Es inadmisible que... Es incierto que...
Es refutable que... Es falaz que... En modo alguno...
3 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

4. Tabla de verdad de la proposición disyuntiva inclusiva A ν B .
o
Otras formas de conexión que nos indican una disyunción inclusiva son:
A menos que 0 en todo caso
Excepto que 0 también
Salvo que 0 incluso
A no ser que 0 bien
Y bien o también Al menos uno de los dos .... o ....
0 sino Alternativamente
4 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

5. Tabla de verdad de la proposición disyuntiva exclusiva A Δ B .
A B A∆B A B A∆B
V V F 1 1 0
V F V 1 0 1
o
F V V 0 1 1
F F F 0 0 0
Alguna formas de conectivos a emplear son:
O...O... ... no equivale a ...
0 bien ... o bien ... No es cierto que...equivale a...
No es equivalente ... con ... 0 solo .... o solo ....
....a menos que solamente... ...salvo que únicamente...
....excepto que sólo.... ....o bien necesariamente....
....o exclusivamente.... ....no es idéntico a....
....no es lo mismo que... Salvo que .... o ....
5 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

6. Tabla de verdad de la proposición conjuntiva A ^ B .
o
En nuestro lenguaje podemos emplear:
Pero Aún cuando No obstante
Sin embargo Al igual que Aunque
Además Tanto …. como …. Más aún
A la vez Siempre ambos…. con….. También
Incluso No sólo….sino también…. Es compatible con
Así como A pesar de Así mismo
Del mismo modo ….con …. los dos a la vez De la misma forma que
6 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

7. Tabla de verdad de la proposición condicional A  B .
o
La manera de expresar la condicional en el orden antecedente-consecuente
("p → q" Implicación directa), son las siguientes:
Si p, entonces q p por tanto q
Siempre que p entonces q p por consiguiente q
p es suficiente para q p por ende q
p implica q p por conclusión q
i
Ya que p bien se ve que q Dado que p por eso q
En cuanto p por tanto q Porque p por eso q
Puede también expresarse en el orden consecuente-antecedente o Implica-
ción Inversa ("q ← p"):
q si p q es implicada para p q de modo que p
q siempre que p q cada vez que p q puesto que p
q es necesario para p q en vista que p q porque p
Sólo si p, q Sólo cuando p, q Solamente porque p, q
q dado que p q ya que p q cada vez que p
q a condición de que p q dado que p q se concluye de p
q supone que p q sigue de p Únicamente si p, q
7 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

8. Tabla de verdad de la proposición bicondicional AB .
o
También se suele emplear expresiones como:
...siempre y cuando... Es suficiente para que suficiente sea
...es equivalente a... Es condición necesaria y suficiente para
...es lo mismo que... ...por lo cual y según lo cual...
...cuando y sólo cuando... ...cada vez que y sólo si...
Si y sólo si p, q ...si de la forma...
...siempre que y sólo cuando... .. .implica y está implicado por...
...es idéntico a... Siempre que ... y siempre que ...
Observemos que el número de renglones de una tabla de verdad es 2n en donde n es
el número de proposiciones simples que aparecen en la proposición compuesta.
8 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

9. USO DE LOS SIGNOS DE AGRUPACIÓN
Los signos de agrupación (paréntesis,
corchetes, llaves) se usan en lógica cuando
se trata de obtener esquemas lógicos más
complejos con el fin de evitar la ambigüedad
en las formulas.
Por ejemplo: p ν q ^ r es ambigua, pero
asociando sus términos (p ν q) ^ r deja de
ser ambigua y tiene sentido.
La otra finalidad de los signos de
agrupación es darle mayor jerarquía a los
conectivos.
9 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

10. ESQUEMAS MOLECULARES
Es la combinación de variables y conectivos lógicos asociados con signos
de agrupación. Los cuales se verifican con las tablas de verdad.
En cada esquema molecular sólo uno de los conectivos es el de mayor
jerarquía y es el que le da nombre a dicho esquema.
Definición 1. Una proposición compuesta es una Tautología si al
construir su tabla de verdad el resultado en cada renglón es verdadero
independientemente de los valores de verdad que tomen las
proposiciones simples que intervienen.
Definición 2. Una proposición compuesta es una Contradicción si al
construir su tabla de verdad el resultado en cada renglón es falso
independientemente de los valores de verdad que tomen las
proposiciones simples que intervienen.
Definición 3. Una proposición compuesta es una Contingencia si al
construir su tabla de verdad no resulta tautología ni contradicción.
10 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

11. Ejemplos
Construir la tabla de verdad de las proposiciones compuestas que se dan e
indicar si se trata de una tautología, contradicción o contingencia.
1. ⌐A ν B
Es una proposición disyuntiva en la que intervienen 2 proposiciones
simples, luego la tabla está formada por cuatro renglones.
A B ⌐A B ⌐AνB
1 1 0 1 1
1 0 0 0 0
0 1 1 1 1
0 0 1 0 1
Por lo tanto es una contingencia
11 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

12. [( A B) ^ ⌐B ] ⌐A
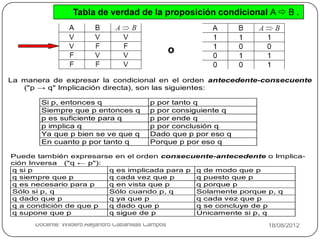
Es una proposición condicional y su tabla es la siguiente.
A B [(AB) ^ ⌐B]  ⌐A
1 1 1 0 0 1 0
1 0 0 0 1 1 0
0 1 1 0 0 1 1
0 0 1 1 1 1 1
Por lo tanto es una Tautología
12 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

13. p q p q p
Es una proposición disyuntiva exclusiva en la que
intervienen 2 proposiciones simples, luego la tabla
está formada así
p q p q p q p
V V V V F F F F F F V V
V F V V V F F F F V V V
F V F F F F V F F F V F
F F F V V V V F V V F F
1 3 2 5 4 R 9 6 8 7
13
Por lo tanto es una Contradicción
Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

14. EJERCICIOS
Verificar el valor de los siguientes esquemas moleculares usando
tablas:
a) ((( p  q) ^ r) ν (r ^ p))
b) ((p  (q ν r)) ^ ((p  r) ^ p)  q));
c) ((⌐(p ^ q)  r) ν p)
d) (⌐((⌐(p)  q) ν r));
e) (⌐(p ν q)  (⌐(p) ^ ⌐(q)))
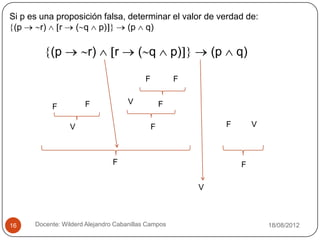
Formalizar el siguiente argumento y encuentre el valor de verdad: Me
gusta el helado de fresa, pero también el de limón. Si hay sólo helado de
chocolate lo comeré, a pesar de que no me guste. Por tanto, no comeré
helado de fresa.
Para formalizar el razonamiento dado, definimos las proposiciones atómicas p = me gusta el
helado de fresa, q = me gusta el helado de limón, r = hay sólo helado de chocolate, s = comeré
helado de chocolate, t = me gusta el helado de chocolate, u = comeré helado de fresa. La
formalización se escribe, como: [ p ^ q ^ (r  s) ^ ⌐ t ] ⌐ u
14 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012

15. EJEMPLO:
Si la proposición:
[p ( q r)] (s q) , es falsa. Determine los valores
de verdad de “p”, “q”, “r” y “s”
[p ( q r)] (s q)
(V V )
F F V
F F ( V )
F
F
F
Por lo tanto los valores de las proposiciones son:
p=F q=V r=V s=V

16. Si p es una proposición falsa, determinar el valor de verdad de:
(p r) r ( q p) (p q)
(p r) r ( q p) (p q)
F F
F V F
F
V F F V
F F
V
16 Docente: Wilderd Alejandro Cabanillas Campos 18/08/2012