Este documento explica cómo construir tablas de verdad. Define proposiciones atómicas y valores de verdad. Explica cómo asignar valores de verdad a proposiciones simples y complejas con diferentes números de proposiciones. También describe cómo resolver tablas de verdad apelando a las tablas de las conectivas lógicas. El documento enfatiza la importancia de distinguir el alcance de las negaciones al construir tablas de verdad.














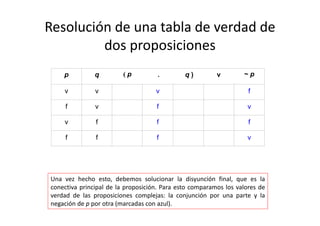
![Resolución de una tabla de verdad de
tres proposiciones
La mecánica para resolver una tabla de tres proposiciones es la misma.
Primero, entonces, asignamos los valores de verdad a las diferentes
proposiciones. En este caso serán 8 filas.
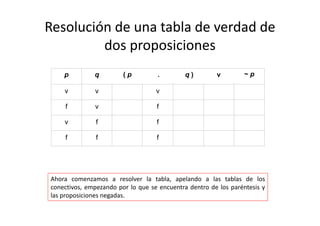
[ ( ~ p → q ) v r ] → p](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-22-320.jpg)
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v
f v v
v f v
f f v
v v f
f v f
v f f
f f f
Se distribuyen los valores según vimos antes en esta presentación.](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-23-320.jpg)
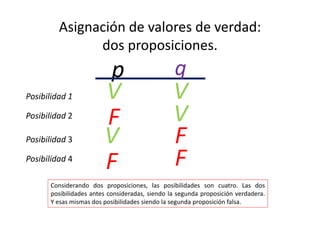
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v f v v v
f v v v v v f
v f v f f v v
f f v v f v f
v v f f v f v
f v f v v f f
v f f f f f v
f f f v f f f
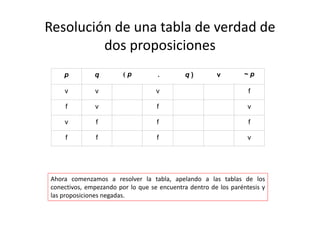
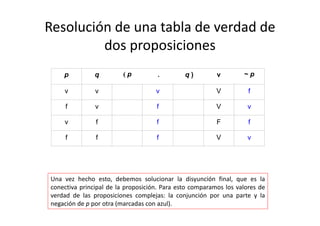
Luego ponemos los valores de verdad en las proposiciones simples negadas
(en rojo). Pueden copiar los valores asignados debajo de cada proposición si
les parece más facil (en azul).](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-24-320.jpg)
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v f v v v v
f v v v v v v f
v f v f v f v v
f f v v f f v f
v v f f v v f v
f v f v v v f f
v f f f v f f v
f f f v f f f f
Ahora solucionamos lo que se encuentra dentro del paréntesis apelando, en
este caso, a la tabla del condicional (en azul).](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-25-320.jpg)
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v f v v v v
f v v v v v v f
v f v f v f v v
f f v v f f v f
v v f f v v f v
f v f v v v f f
v f f f v f f v
f f f v f f f f
Ahora debemos solucionar la conectiva principal de la proposición entre
corchetes, comparando los valores de verdad de la disyunción (en azul). Para
no confundirse, pueden ir tachando lo que ya utilizaron.](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-26-320.jpg)
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v f v v v v v
f v v v v v v v f
v f v f v f v v v
f f v v f f v v f
v v f f v v v f v
f v f v v v v f f
v f f f v f v f v
f f f v f f f f f
La solución de la disyunción se encuentra en rojo.](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-27-320.jpg)
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v f v v v v v
f v v v v v v v f
v f v f v f v v v
f f v v f f v v f
v v f f v v v f v
f v f v v v v f f
v f f f v f v f v
f f f v f f f f f
Ahora debemos solucionar el valor de verdad de la conectiva principal de la
proposición, que en este caso es un condicional. Para eso debemos comparar
los valores en azul.](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-28-320.jpg)
![Resolución de una tabla de verdad de
tres proposiciones
p q r [ ( ~ p → q ) v r ] → p
v v v f v v v v v v
f v v v v v v v f f
v f v f v f v v v v
f f v v f f v v f f
v v f f v v v f v v
f v f v v v v f f f
v f f f v f v f v v
f f f v f f f f v f
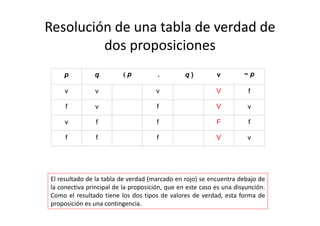
El resultado de la tabla se encuentra en rojo. Como puede verse, también se
trata de una contingencia. Si en el resultado fuesen todos verdaderos, sería
una tautología, si fuesen todos falsos, una contradicción.](https://image.slidesharecdn.com/confeccintablasdeverdad2014-140421192725-phpapp01/85/Confeccion-tablas-de-verdad-2014-29-320.jpg)






