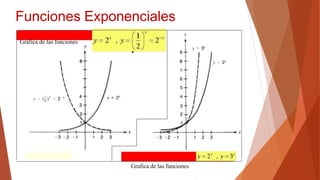
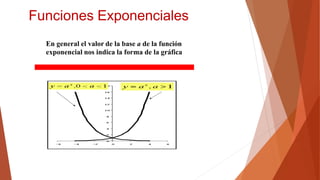
El documento aborda las funciones exponenciales y logarítmicas, definiendo y ejemplificando cada tipo, así como sus propiedades y gráficos relacionados. Se explican las leyes de los logaritmos y su aplicación en la evaluación de expresiones y resolución de ecuaciones exponenciales y logarítmicas. Además, se incluyen normas y ejemplos para resolver este tipo de ecuaciones, tanto algebraicamente como gráficamente.

1. Clase Demostrativa
Funciones Exponenciales y
Logarítmicas

2. Temas:
• Funciones exponenciales.
• Funciones logarítmicas.
• Leyes de los logaritmos.
• Ecuaciones exponenciales y
logarítmicas.

3. Funciones Exponenciales
La función exponencial con base a se define para todos
los números reales x por:
Base 2 Base 3 Base 10
Base (1/2)
con a > 0 , a ≠ 1
Ejemplos de funciones exponenciales:
D
e
f
i
n
i
c
i
ó
n

4. Ejemplo :
Sea y evalúe lo siguiente:
  x
x
f 3

 
2
) f
a








3
2
) f
b
 
2
) f
c
9
32

4807
.
0
3 3
2


7288
.
4
3 2


5. Ejemplos: sea la función f(x) = 3 x , para obtener su gráfica le
damos valores a x y obtenemos el valor de f
Funciones Exponenciales
x f (x) = 3 x
-3 3 - 3 = 0.037
- 2 3 – 2 = 0.111
- 1 3 – 1= 0.333
0 3 0 = 1
1 3 1 = 3
2 3 2 = 9
3 3 3 = 27

6. Funciones Exponenciales
Gráfica de las funciones
Grafica de las funciones

7. En general el valor de la base a de la función
exponencial nos indica la forma de la gráfica
Funciones Exponenciales

8. Función Exponencial Natural
La función exponencial natural es la función exponencial de base e
El número e es un número irracional cuyo valor es
aproximadamente 2.7182818284590452353602
Funciones Exponenciales
El número e es un interesante número que tiene
que ver con la naturaleza, la ciencia y la tecnología.
Apartir de e se determina la ecuación de la curva
de un puente colgante , el tiempo de enfriamiento
de un cuerpo , la antigüedad de la materia orgánica
por desintegración del carbono 14, el crecimiento
de la población, el interes compuesto, entre otras.
Recordar que las características de esta función
son las mismas que la función exponencial
para a > 1
(0,1)
Gráfica de

9. De las gráficas anteriores podemos deducir las siguientes
propiedades de la función exponencial:
 Dominio todos los números reales
 El rango es el intervalo de ( 0, ∞ )
 Es continua
 f ( 0 ) = 1 para cualquier valor de a
 f ( 1 ) = a para cualquier valor de a
 Si a > 1, la función es creciente
 Si 0 < a < 1, la función es decreciente.
Funciones Exponenciales

10. D
e
f
i
n
i
c
i
ó
n
FUNCIONES LOGARÍTMICAS
 Sea a un número positivo con . La función logarítmica con
base a, denotada por
, se define
Así, es el exponente al que se debe elevar la base a para dar
x.
1

a
a
log
x
a
y
x y
a 


log
x
a
log

11. Propiedad de los logarítmos
Propiedad Razón
Se debe elevar a a la potencia 0
para obtener 1.
Se debe elevar a a la potencia 1
para obtener a.
Se debe elevar a a la potencia x
para obtener .
es la potencia a la cual
se debe elevar a para obtener x.
x
a
x
a
log
0
1
log 
a
1
log 
a
a
x
ax
a 
log
x
a x
a

log

12. Comparando la forma Exponencial y la forma Logarítmica tenemos
Exponencial: Logarítmica:
Base
Exponente
Base
Exponente
En ambas formas la base a es la misma
FUNCIONES LOGARÍTMICAS

13. Forma
Logarítmica
Forma
Exponencial
EJEMPLO:
FUNCIONES LOGARÍTMICAS

14. Ejemplo : Trazar la gráfica de la función f(x) = log2 x
Para construir una tabla de valores, elegimos los valores de x
como potencias de 2, de modo que sea más facil hallar sus
logaritmos.
x f (x) =
log2
x
2 - 3 = 0.125 - 3
2 – 2 = 0.25 - 2
2 – 1= 0.5 - 1
2 0 = 1 0
2 1 = 2 1
2 2 = 4 2
2 3 = 8 3
FUNCIONES LOGARÍTMICAS

15.  Logarítmo natural
 El logarítmo con base e se llama logarítmo natural y se denota
por:
 f(x) = ln x
 La función logarítmo natural y = ln x es la función inversa de la
función exponencial:
FUNCIONES LOGARÍTMICAS

16. Propiedades de los logarítmos naturales
Propiedad Razón
x
e
x
e
e
x
x




ln
ln
1
ln
0
1
ln Se tiene que elevar e a la potencia 0
para obtener 1.
Se tiene que elevar e a la potencia 1
para obtener e.
ln x es la potencia a la cual e debe
ser elevada para obtener x.
Se tiene que elevar e a la potencia x
para obtener .
x
e

17. De las gráficas anteriores podemos deducir las siguientes
propiedades de la función logarítmica:
 Dominio todos los números reales positivos
 El rango es el intervalo de ( -∞, ∞ )
 Es continua
 f ( 1 ) = 0 para cualquier valor de a
 f ( a ) = 1 para cualquier valor de a
 Si a > 1, la función es creciente
 Si 0 < a < 1, la función es decreciente.
FUNCIONES LOGARÍTMICAS

18. 18
Funciones Logarítmicas

19. Leyes de los logarítmos
19
En esta sección se estudian las propiedades de
los logarítmos. Estas propiedades dan a las
funciones logarítmos una amplia variedad de
aplicaciones.
Ya que los logarítmos son exponentes, las leyes
de los exponentes dan lugar a las leyes de los
logarítmos.

20. Leyes de los logarítmos
20
Leyes de los logarítmos
Sea a un número positivo, con . Sea A, B y C números
reales cualesquiera con .
Ley Descripción
1

a
0
0 
 yB
A
  A
C
A
B
A
B
A
B
A
AB
a
c
a
a
a
a
a
a
a
log
log
)
3
log
log
log
)
2
log
log
)
(
log
)
1










 El logarítmos de un producto de
números es la suma de los
logarítmos de los números.
El logarítmo de un cociente de
números es la diferencia de los
logarítmos de los números.
El logarítmo de una potencia de
un número es el exponente
multiplicado por el logarítmo de
número.

21. Ejemplo
Uso de las leyes de los logarítmos para evaluar expresiones
21
Evalúe cada expresión:
8
log
3
1
)
5
log
80
log
)
32
log
2
log
)
2
2
4
4



c
b
a

22. Ejemplo
Uso de las leyes de los logarítmos para evaluar expresiones
3
64
log
)
32
.
2
(
log
4
4



32
log
2
log
) 4
4 
a
B
A
AB a
a
a log
log
)
(
log
)
1 

Propiedad utilizada:

23. Ejemplo
Uso de las leyes de los logarítmos para evaluar expresiones
23
5
log
80
log
) 2
2 
b
4
16
log
5
80
log
2
2



B
A
B
A
a
a
a log
log
log
)
2 







Propiedad utilizada:

24. Ejemplo
Uso de las leyes de los logarítmos para evaluar expresiones
24
8
log
3
1
) 
c
301
.
0
)
2
log(
)
1
log(
2
1
log
2
1
2
1
8
1
8
1
log
8
log
3 3
3
3
1
3
1

























  A
C
A a
c
a log
log
)
3 
Propiedad utilizada:

25. Ejemplo
Expandir expresiones logarítmicas
Use las leyes de logarítmos para expandir o desarrollar cada
expresión.
 






3
6
3
5
2
ln
)
log
)
)
6
(
log
)
c
ab
c
y
x
b
x
a
c
b
a
c
b
a
c
ab
y
x
y
x
x
ln
3
1
ln
ln
ln
ln
ln
ln
)
ln(
log
6
log
3
log
log
log
6
log
3
1
3
5
5
3
5
3
5
2
2















26. Ejemplo
Combinar expresiones logarítmicas
)
1
log(
2
1
log
3
) 
 x
x
a
Combinar en un solo logarítmo, la siguiente expresión:
2
1
3
2
1
3
)
1
(
log(
)
1
log(
log





x
x
x
x
)
1
ln(
4
ln
2
1
ln
3
) 2


 t
t
s
b
  

















4
2
3
4
2
2
1
3
4
2
2
1
3
1
ln
)
1
ln(
)
ln(
)
1
ln(
ln
ln
t
t
s
t
t
s
t
t
s

27. Ecuaciones
exponenciales y logarítmicas
 Una ecuación exponencial es aquella en la que la variable ocurre en el
exponente.
 Por ejemplo:
 La variable x representa una dificultad por que esta en el exponente.
Para tomar este caso se toma el logarítmo en cada lado y luego se
usan las reglas de los logarítmos.
Veamos:
27
7
2 
x

28. Ecuaciones
exponenciales y logarítmicas
28
7
ln
2
ln
7
ln
2
ln


x
x
807
.
2
2
ln
7
ln


x
7
2 
x
Recuerde la regla 3

29. Normas para resolver ecuaciones exponenciales
1) Aísle la expresión exponencial en un lado de la
ecuación.
2) Tome el logarítmo de cada lado, luego utilice las leyes
de los logarítmos para “bajar el exponente”.
3) Despeje la variable.
29

30. Ejemplo
Resolver una ecuación exponencial
Encuentre la solución de:
Solución:
7
3 2


x
7
log
)
3
log( 2


x
7
3 2


x
7
log
3
log
)
2
( 

x
3
log
7
log
)
2
( 

x
228756
.
0
2
3
log
7
log




x
Si verificas en tu calculadora:
7
3 2
)
228756
.
0
(




31. 31
Ejemplo
Una ecuación exponencial de tipo cuadrático
Resuelva la ecuación:
Solución:
0
6
2


 x
x
e
e
0
6
2


 x
x
e
e
0
6
)
( 2


 x
x
e
e
0
)
2
)(
3
( 

 x
x
e
e
0
3 

x
e o 0
2 

x
e
3

x
e 2


x
e

32. 32
Ejemplo
Resolver una ecuación exponencial
Resuelva la ecuación:
Solución: Primero se factoriza el lado izquierdo de la ecuación.
0
3 2

 x
x
e
x
xe
0
)
3
( 
 x
xex
0
3 2

 x
x
e
x
xe
0
)
3
( 
 x
x
Se divide entre
x
e
0

x 0
3 
 x
3


x
Las soluciones son:

33. 33
Ecuaciones Logarítmicas
Una ecuación logarítmica es aquella en la ocurre un logarítmo de la
variable.
5
)
2
(
log2 

x
30
2
32
2
2 5





x
Para despejar x, se escribe la ecuación en forma exponencial.
Otra forma de considerar el primer paso es elevar la base, 2, a cada
la de ecuación.
5
)
2
(
log
2
2 2


x
5
2
2 

x
30
2
32 


x
Los pasos se resumen a continuación.

34. 34
Normas para resolver ecuaciones logarítmicas
1) Aísle el término logarítmico en un lado de la ecuación;
podría ser necesario combinar primero los términos
logarítmicos.
2) Escriba la ecuación en forma exponencial (o eleve la base a
cada lado de la ecuación).
3) Despeje la variable.

35. 35
Ejemplo
Resolver ecuaciones logarítmicas
De cada ecuación despeje x.
3
)
25
(
log
)
8
ln
)
2 


x
b
x
a
8
ln 
x
8
e
x 
2981

x
3
2
7
25 

8
25 
 x
17
8
25 


x

36. 36
Ejemplo
Resolver una ecuación logarítmica de manera
algebraica y gráfica
Resuelva la ecuación (1): 1
)
1
log(
)
2
log( 


 x
x
  1
)
1
)(
2
(
log 

 x
x
10
)
1
)(
2
( 

 x
x
10
2
2


 x
x
0
12
2


 x
x
0
)
3
)(
4
( 

 x
x
3
,
4 

 x
x