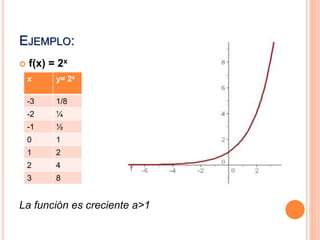
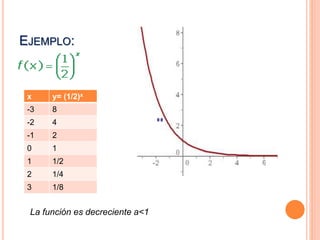
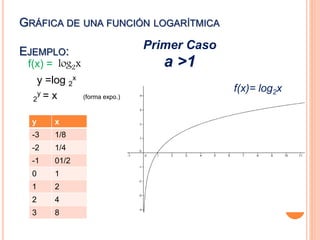
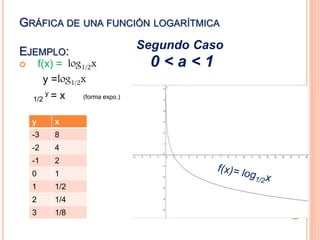
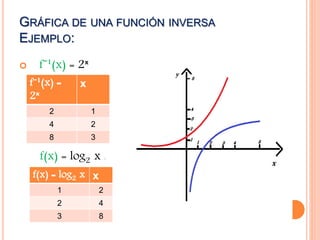
Este documento describe las funciones exponenciales y logarítmicas. Explica que una función exponencial toma la forma f(x)=ax, donde a es la base positiva. Las funciones exponenciales son crecientes si a>1 y decrecientes si a<1. La función logarítmica es la inversa de la función exponencial, definida como logax=y si y solo si ax=y. Las funciones logarítmicas son crecientes si a>1 y decrecientes si a<1.

1. FUNCIONES EXPONENCIALES Y
LOGARITMICAS

2. FUNCIONES EXPONENCIALES
 La función exponencial f con base a se define
como: f(x)= ax
 Sea a un número real positivo.
 La función que a cada número real x le hace
corresponder la potencia ax
 En donde x es cualquier numero real.

3. PROPIEDADES DE LAS POTENCIAS
 Antes de dar un ejemplo de función exponencial,
conviene recordar algunas propiedades de las
potencias:
1- a° = 1
2- a-n = 1/an

4. PROPIEDADES DE LA FUNCIÓN EXPONENCIAL Y = A X
Las funciones exponenciales pasan por el punto (0,1)
 1. Para x = 0, la función toma el valor 1: f(0) = a° = 1
 2. Para x = 1, la función toma el valor a: f(1) = a¹ = a
 3. La función es positiva para cualquier valor de x: f(x) >0.
Esto es debido a que la base de la potencia, a, es
positiva, y cualquier potencia de base positiva da como
resultado un número positivo.
 4 . Si la base de la potencia es mayor que 1, a>1, la
función es creciente.
 5. Si la base de la potencia es menor que 1, a<1, la
función es decreciente

5. EJEMPLO:
 f(x) = 2x
x y= 2x
-3 1/8
-2 ¼
-1 ½
0 1
1 2
2 4
3 8
La función es creciente a>1

6. EJEMPLO:
x y= (1/2)x
-3 8
-2 4
-1 2
0 1
1 1/2
2 1/4
3 1/8
La función es decreciente a<1

7. LAS FUNCIONES EXPONENCIALES SON
BIUNÍVOCAS.
 Deben cumplir con las siguientes condiciones
1.- Si x1 = x2 entonces ax1 = ax2
2.- Si ax1 = ax2 entonces x1 = x2
 Ejemplo: Resuelva la ecuación: 3 5x-8 = 9 x+2
 3 5x-8 = 9 x+2
3 5x-8 = (32) x+2
3 5x-8 = 32x+4
5x-8 = 2x+4
5x -2x =4+8
3x = 12
x= 4

8. FUNCIONES LOGARÍTMICAS
 La inversa de una función exponencial de base a,
se llama logarítmica de base a y se representa por
log ax
 Se expresa de la siguiente manera:
y =loga(x) Si y solo si x= ay
Formas Equivalentes
Forma Logarítmica Forma Exponencial
log5 u = 2 52 = u
logb 8 = 3 b3 = 8
r = logp q pr =q
w = log4 (2t + 3) 4w = 2t + 3
log3 x = 5 + 2z 35+2z = x

9. EJEMPLOS
Hallar los logaritmos de:
 log10 100= 2 porque 102 = 100
 log1/32 = -5 porque 2-5 = 1/32
 log9 3 = ½ porque 91/2 = 3
 log7 1= 0 porque 70 = 1
 log3 (-2) no es posible porque 3y = -2

10. GRÁFICA DE UNA FUNCIÓN LOGARÍTMICA
EJEMPLO:
f(x) = log2x
y =log 2
x
2
y = x (forma expo.)
y x
-3 1/8
-2 1/4
-1 01/2
0 1
1 2
2 4
3 8
Primer Caso
a >1
f(x)= log2x

11.  El dominio es R+
 El logaritmo de 1 es 0
 El logaritmo de la base es 1. la curva pasa por el punto (a,1)
 Si a = 2 , pasa por el punto (2,1)
 Los logaritmos de números mayores
 Los logaritmos de número mayores que 1 son positivos y
crecen indefinidamente en la medida que crece x
 x > 1 f(x)> 0 (creciente)
 Lo logaritmos de los numero menores que 1 son negativos y
decrece indefinidamente al decrecer x
 x < 1 f(x)< 0
 Como al crecer x también crece f(x), decimos que la
FUNCION ES CRECIENTE

12. GRÁFICA DE UNA FUNCIÓN LOGARÍTMICA
EJEMPLO:
 f(x) = log1/2x
y =log1/2x
1/2
y = x (forma expo.)
y x
-3 8
-2 4
-1 2
0 1
1 1/2
2 1/4
3 1/8
Segundo Caso
0 < a < 1

13.  Dominio R+
 El logaritmo de la base es 1. la curva pasa por el punto (a,
1)
Si la base es 1/2 , la curva pasa por (1/2, 1)
 El logaritmo de 1 es 0. la curva pasa por el punto (1,0)
 Los logaritmos de números mayores que 1 son negativos y
decrecen indefinidamente al crecer x
 x > 1 f(x)< 0
 los logaritmos de los numero menores que 1 son positivos
y crecen indefinidamente al decrecer x
 x< 1 f(x) > 0
 Como al crecer x, decrece f(x), decimos que la FUNCION
ES DECRECIENTE

14. FUNCIONES INVERSAS
La función logarítmica tiene la forma general:
f(x) = log ₐ X
Y su función inversa es :
f ˉ¹(x) = aˣ
Ejemplo:
La inversa de la función f (x )= log2 x es la
función f ˉ¹(x) = 2 ˣ
Respecto a esto se arma una tabla de valores.

15. GRÁFICA DE UNA FUNCIÓN INVERSA
EJEMPLO:
 fˉ¹(x) = 2ˣ
fˉ¹(x) =
x
2ˣ
2 1
4 2
8 3
f(x) = log2 x :
f(x) = log2 x x
1 2
2 4
3 8