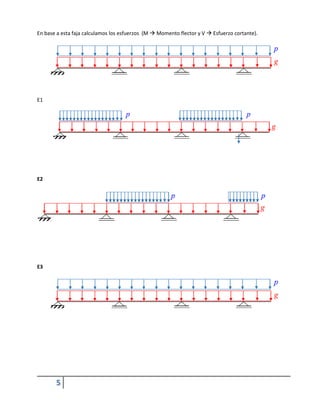
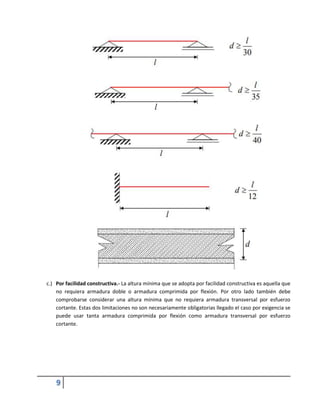
Este documento describe losas de hormigón armado, incluidas las losas macizas armadas en una y dos direcciones. Explica que las losas son elementos estructurales bidimensionales que soportan cargas perpendiculares a su plano. También cubre el cálculo de esfuerzos, disposición de armaduras, espesores mínimos y otros aspectos de diseño de losas.

1. 1
2.- Losas de Hormigón Armado
2.1 Introducción
Las losas son elementos estructurales bidimensionales, limitadas por dos planos paralelos de separación “h”,
siendo el espesor “h” pequeño comparado con las otras dos dimensiones básicas. Las cargas que actúan sobre
el plano medio de la losa, son esencialmente perpendiculares al plano principal de las mismas, por lo que su
comportamiento está dominado por la flexión.
2.2 Cargas que actúan sobre losas.
Por lo general las cargas que actúan sobre las losas para el cálculo son consideradas uniformemente
repartidas en su área y se las divide en cargas permanentes (g) y cargas variables (p)
Las cargas variables son de diversa índole y dependen de la función que preste la losa. Estas acciones o cargas
varían su intensidad significativamente con el tiempo, debidos al peso de las personas, vehículos, muebles
etc.
Las cargas permanentes son aquellas cuya intensidad varía poco en el tiempo y corresponden al peso propio
de la losa y a todos los elementos que están rígidamente vinculados a ellas como ser: pisos, contrapisos, cielo
raso, cielo falso, etc.

2. 2
2.3 Losas Macizas Generalidades.
Son elementos estructurales en los cuales dos de sus dimensiones predominan sobre la tercera (su espesor),
formando un elemento plano. En la mayoría de los casos las cargas son normales al plano de las mismas,
estando solicitadas predominantemente por “ESFUERZOS DE FLEXIÓN”.
Su función en una estructura es la de recibir las cargas y trasmitirlas hacia sus apoyos (vigas).De acuerdo a la
forma de trasmitir las cargas hacia los apoyos las podemos dividir o clasificar en dos tipos:
-Losasarmadasenunadirección.
-Losasarmadasendosdirecciones.
Las losas tienen el inconveniente de su excesivo peso propio por lo que su uso se limita a luces muy pequeñas
en el caso de losas de entre piso.
2.3.1 Losas Macizas Armadas en una dirección.
Hay dos razones por las cuales la losa resulta armada en una dirección:
• Cuando los elementos de apoyo de la losa son paralelos lo cual nos obliga a apoyar las losas en el sentido
perpendicular a los elementos de apoyo.

3. 3
• Cuando se tienen apoyos en todo el contorno de una losa la podemos armar en una sola dirección siempre
y cuando la relación de luces sea mayor a 2,
𝑙 𝑚𝑎𝑦𝑜𝑟
𝑙 𝑚𝑒𝑛𝑜𝑟
> 2 .

4. 4
2.3.1.1 Losas apoyadas sobre cuatro bordes.
Condición
Si
𝑳 𝒚
𝑳 𝒙
> 2 Armar la Losa en una dirección (luz menor)
𝑺𝒊
𝑳 𝒚
𝑳 𝒙
< 2 Armar la losa en dos direcciones (Ly,Lx)
2.3.1.2 Obtención de esfuerzos.
Para obtener los esfuerzos de una losa armada en una dirección, se toma una faja de ancho unitario según la
dirección de armado, en base a la cual usando cualquier método elástico se puedan obtener los diagramas de
fuerza (flexión y esfuerzo cortante). Para distintos estados de carga desfavorable superponemos los
diagramas de esfuerzo de cada estado de carga logrando la envolvente en base a la cual se determinarán las
armaduras y se efectuará la respectiva disposición de la misma.

5. 5
En base a esta faja calculamos los esfuerzos (M → Momento flector y V → Esfuerzo cortante).
E1
E2
E3

6. 6
2.3.1.3 Calculo de la armadura principal.
La armadura principal se obtiene por flexión simple para secciones rectangulares donde la altura total es el
espesor de la losa y la base es el ancho unitario de la faja considerada.
Esta armadura nunca deberá ser menor que la armadura mínima siguiente:
𝐴 𝑚𝑖𝑛=
1.5
1000
𝐵 d (por temperatura y retracción).
𝐴 𝑚𝑖𝑛= 0.04Bd
𝑓 𝑐𝑑
𝑓 𝑦𝑑
(por flexión)
2.3.1.4 Disposición de las armaduras.
Las armaduras se disponen de la siguiente manera:
a.) Armadura de tramo.
En las armaduras de tramo, la mitad se lleva de apoyo a apoyo y la otra mitad una vez que ya no es
necesaria para absorber los momentos positivos se levantan con una inclinación de 45 grados y se los
lleva a la zona superior de los apoyos, con el objeto de que esta armadura absorba parte de los
momentos negativos de los apoyos internos de la losa continua o sirvan para cubrir momentos
imprevistos de empotramiento logrando plastificar el apoyo exterior materializando la rótula,
evitando fisuración en los apoyos externos.
b.) Armadura de apoyo.
Si la armadura levantada de los tramos no absorbe la armadura requerida por los apoyos, se dispone
una armadura suplementaria que cubre la totalidad de la armadura requerida por los apoyos y por
los momentos flectores en los apoyos.
- Losa Simplemente Apoyada

7. 7
Evitar la fisura materializa la rotura plastificada
- Losa continua
𝑨 𝟏 → 𝜇
𝑑=
𝛾 𝑓×𝑀1
1×𝑑2×𝑓 𝑐𝑑
𝑨(−)
→ 𝝁
𝒅=
𝜸 𝒇×𝑴 𝟑
(−)
𝟏×𝒅 𝟐×𝒇 𝒄𝒅
1.3.1.5 Armadura transversal de repartición.
En el sentido perpendicular a las armaduras principales se colocaran unas armaduras llamadas de repartición
que tiene por finalidad vincular en el sentido longitudinal a la losa, uniendo las distintas fajas que
teóricamente se las ha dividido, de tal manera que cuando actúa una carga aislada sobre una faja imaginaria
las demás fajas contribuyen también a soportarla, dicho de otra forma la vinculación provista de armadura
de repartición asegura la participación de zonas vecinas en la absorción de cargas, por otro lado esta
armadura toma también esfuerzo secundarios por temperatura y por retracción, de no disponerse la
armadura de repartición podrían aparecer grandes grietas paralelas a la armadura principal.
La armadura de repartición deberá ser al menos la quinta parte de la armadura principal (20%) y nunca inferior
a Ø6 cada 25.

8. 8
Para el esfuerzo cortante normalmente lo que se tiene que realizar es verificar que el hormigón solo lo
absorba, de no hacerlo se tendrá que poner armadura transversal hasta absorber el esfuerzo cortante dado.
𝑓𝑣𝑑=0.5 √𝑓𝑐𝑑 (kp/𝑐𝑚2
)
1. Si el hormigón absorbe el esfuerzo cortante no es necesaria la armadura transversal.
Vd ≤ 𝑓𝑣𝑑(100)d
2. Si el esfuerzo cortante de cálculo es mayor al esfuerzo de contribución del hormigón es preciso
colocar armadura transversal.
Vd > 𝑓𝑣𝑑(100)d
2.3.1.5 Espesores mínimos.
Para pre dimensionar el espesor de una losa armada en una dirección tenemos los siguientes criterios:
a.) Por norma.- Según CBH-87, Con respecto a los espesores mínimos, para los casos normales pueden
adoptarse los siguientes:
- 5 cm; si no existen cargas concentradas; por ejemplo, placas para cubiertas no accesibles
- 7 cm; si las acciones preponderantes son distribuidas o estáticas
- 10 cm; si una parte moderada de las acciones es concentrada y dinámica; por ejemplo, placas
accesibles a vehículos de turismo
- 12 cm; si una parte importante de las acciones es concentrada y dinámica; por ejemplo, placas
accesibles a vehículos pesados.
- 15 cm; placas sobre apoyos puntuales.
b.) Por deformación.- La altura útil de una losa llena armada en una sola dirección que satisface la
deformación deberá cumplir con las siguientes relaciones que son válida para losa pertenecientes a
construcciones corrientes.

9. 9
c.) Por facilidad constructiva.- La altura mínima que se adopta por facilidad constructiva es aquella que
no requiera armadura doble o armadura comprimida por flexión. Por otro lado también debe
comprobarse considerar una altura mínima que no requiera armadura transversal por esfuerzo
cortante. Estas dos limitaciones no son necesariamente obligatorias llegado el caso por exigencia se
puede usar tanta armadura comprimida por flexión como armadura transversal por esfuerzo
cortante.

10. 10
2.3.1.6 Separación de las barras.
La separación de las armaduras principales debe cumplir las siguientes condiciones:
No debe ser mayor a 1.5 del espesor de la losa
No debe ser mayor a 20 cm
En todos los casos, el diámetro no debe ser superior a la décima parte del espesor de la losa
2.3.1.7 Recubrimientos.
Si la losa está protegida el recubrimiento mínimo libre es de 1 cm. Si la losa se encuentra expuesta a la
intemperie aumenta a 1.5 cm y si la losa está en contacto con tierra húmeda el recubrimiento mínimo es 4
cm, pudiendo aumentar hasta los 7 cm según la presencia de humedad en el terreno.
2.3.2 Losas macizas armadas en dos direcciones.
Cuando una losa tiene apoyo en sus cuatro bordes y la relación de luces es menor que 2 comienza a adquirir
importancia la curvatura longitudinal y la losa se ve solicitada en ambas direcciones.
Si tenemos una losa cuadrada con igual tipo de apoyo en sus cuatro bordes, los momentos en las dos
direcciones paralelos a sus lados son iguales, en el centro de la losa y en todos los puntos ortogonalmente
simétricos.
Si hacemos aumentar uno de sus lados el momento en el sentido de la luz menor se va incrementando con
respecto de la luz mayor esto se debe a que la luz menor tiene menor rigidez que en el sentido de la luz
menor.
Si Ly = Lx → My = Mx
Si Ly > Lx → My < Mx

11. 11
2.3.2.1 Calculo de las solicitaciones.
Actualmente existen dos métodos desarrollados para el cálculo de los esfuerzo en losas armadas en dos
direcciones:
1. Método elástico que sigue la teoría matemática de la elasticidad es el más usual en la actualidad.
2. Método plástico toma en cuenta líneas de rotura y asume un comportamiento plástico de la losa
antes de la rotura.
2.3.2.2 Hipótesis básica requerida por la teoría de la elasticidad.
a.) El material que constituye la losa se comporta como homogéneo, isótropo y elástico entre los límites
de carga de servicio siendo por ello valida la ley de Hooke.
b.) La losa tiene que tener un espesor suficiente respecto a sus otras dimensiones como para ofrecer
resistencia a la flexión y no comportarse como membrana.
c.) La fecha en un punto cualquiera de una losa es muy pequeña respecto a su espesor.
d.) La losa no experimenta variaciones de espesor debido a la deformación.
e.) Las leyes de la flexión simple contenida en las hipótesis de Navier – Bernouli son validas (las
deformaciones se mantienen planas antes, durante y después del cargado).
En realidad las losas son las únicas estructuras que se pueden calcular por dos métodos: método plástico y
método elástico porque es un método flexible.
Si analizamos un paralepipedo elemental de una losa armada en dos direcciones se puede ver que en cada
dirección se generan tres tensiones que son:

12. 12
Se observan 6 esfuerzos, 3 en cada cara:
Fx; Fy Son Tensiones normales que dan origen a los momentos Mx y My respectivamente.
Τxz; Τyz; Son Tensiones Tangenciales Verticales que dan origen a los esfuerzos cortantes Vx y Vy
respectivamente.
Τxy; Τyx; Son Tensiones Tangenciales Horizontales que dan origen a los momentos torsores Mxy y Myx
respectivamente.
Si integramos cada una de las tensiones en toda la altura H del paralepipedo veremos lo siguiente al integrar
𝜎 𝑥 genera un momento flector Mx, lo mismo ocurre al integrar 𝜎 𝑦 generando momento flector My.

13. 13
Si integramos la tensión tangencial 𝜏 𝑥𝑧 vereos que se genera un esfuerzo cortante Vx, ocurre lo mismo en la
dirección Y donde 𝜏 𝑦𝑧 genera esfuerzo cortante Vy.
Por ultimo si integramos la tensión tangencial horizontal 𝜏 𝑥𝑦 en toda la altura de la losa veremos que se
genera un momento torsor Mxy lo mismo ocurre para el esfuerzo cortante 𝜏 𝑦𝑥 que genera momento torsor
Myx
Resumiendo podemos indicar que en un punto de una losa armada en dos direcciones se presentan seis
esfuerzos que son: dos momentos flectores uno por cada dirección, dos esfuerzos cortantes uno por cada
dirección, 2 momentos torsores uno por cada dirección.

14. 14