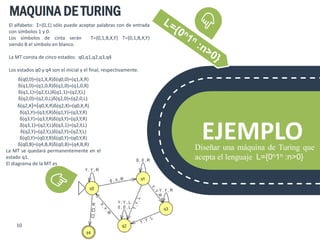
Este documento describe la máquina de Turing, un modelo matemático de computación introducido por Alan Turing en 1937. Explica qué es una máquina de Turing, sus componentes, tipos, definición formal, teoremas, cómo funciona, diagramas y provee un ejemplo de una máquina de Turing que acepta el lenguaje 0n1n.

1. Informe de actividad para WebQuest
AUTÓMATAS LENGUAJES FORMALES
1
MAQUINA DE TURING
Por: Manuel Torres Rivas
C.I: 26.561.400
Sección SAIA A
Prof. Edecio Freitez
Universidad Fermín Todo
Facultad de Ingeniería
Escuela de Computación

2. CONTENIDO
MAQUINA DE TURING
6
5
4
3
2
1
Definiciones Funcionamiento
y características
Tipos de
Máquina de
Turing
Definición formal
Teoremas Diagrama y ejemplo
En 1937, el matemático inglés Alan Turing publicó otro
artículo famoso (sobre los Números Calculables), que
desarrollo el teorema de Gödel y que puede considerarse
el origen oficial de la informática teórica. En este artículo
introdujo la Máquina de Turing, una entidad matemática
abstracta que formalizó el concepto de algoritmo,
convirtiéndose en la precursora de las computadoras
digitales. Con la ayuda de su máquina, Turing pudo
demostrar que existen problemas irresolubles, tales que
ninguna máquina u ordenador serán capaces de obtener su
solución. Por esta razón, Turing es considerado el padre de
la teoría de la computación.

3. 01 02
0301
La máquina de Turing es
un dispositivo informático que
consiste en un cabezal
de lectura y escritura, y de una
cinta de papel que atraviesa la
máquina. Esta cinta se
encuentra divida en cuadrados,
y cada uno de ellos tiene al
mismo tiempo un símbolo. Esta
cinta es la encargada
del almacenamiento de la
máquina, como vehículo
de entrada y salida, además de
funcionar como memoria de
trabajo para almacenar los
resultados de los pasos
intermedios del cálculo.
02
La máquina es
un módulo de reconocimiento de
lenguaje más general que cualquier
autómata finito y de pila, pues tiene
la capacidad de reconocer los
lenguajes regulares y,
los independientes de contexto,
además de muchos otros tipos de
lenguajes.
03
La máquina de Turing ha sido utilizada como:
• Generadora de lenguajes, pues este tipo de máquina posee varias cintas incluyendo una
cinta de salida que al inicio está vacía y luego se va llenando con palabras de lenguaje.
• En compiladores I y II, máquinas de estado, máquinas autómatas y generadores de códigos.
• En la antigüedad fue utilizado en máquinas como la “Bombe” para poder descifrar señales
cifradas por la máquina alemana “enigma” durante la Segunda Guerra Mundial. También
en las máquinas “colossus” que descifraban los mensajes cifrados interceptados en las
comunicaciones de los nazis.
DEFINICIONES
MAQUINA DE TURING
USO
QUE ES
DEFINICIÓN

4. FUNCIONAMIENTO
CaracterísticasEstá formada por un alfabeto de entrada y uno de
salida y por un símbolo especial llamado blanco.
La máquina está conformada por
un alfabeto de entrada y uno de
salida, por un símbolo
especial conocido con el nombre de
blanco el cual normalmente se
representa por medio de una b, Δ o 0,
por un grupo de estados finitos y por
un conjunto de transiciones entre
estos estados.
Su funcionamiento se fundamenta en
la transición, la cual se encarga de recibir
un estado inicial y una cadena de
caracteres los cuales pertenecen al
alfabeto de entrada. A partir de ese
momento la máquina empieza a leer
una celda de la cinta, borrando el
símbolo, y escribiendo el nuevo símbolo
que pertenece al alfabeto de salida para
luego avanzar a la izquierda o a la
derecha, un tiempo a la vez y repitiendo
el proceso según se indique en la
función de transición. Al final del proceso
se detiene en un estado de aceptación,
representando así la salida.
La máquina de Turing funciona por medio de
un control finito, una cabeza lectora y
una cinta por en la cual puede haber
diferentes caracteres, y en la cual se
encuentra la palabra de entrada. Hacia el
lado derecho la cinta tiene una longitud que
es el lugar donde se llenan los espacios con el
carácter blanco el cual es representado por la
letra “t”. Hacia su lado izquierdo pasa lo
contrario pues la cinta no es infinita razón por
la cual hay un cuadro de la cinta que es el
extremo izquierdo. Además, tiene una cabeza
que se mueve hacia la izquierda y derecha,
por lo que tiene la capacidad de pasar en
ciclos repetidos sobre un mismo segmento de
la cinta.
La entrada que tiene la cinta antes de que
comience el cálculo debe consistir en un
número finito de símbolos.
La cinta de la máquina tiene una de longitud
ilimitada.
El cabezal de lectura y escritura puede ser
programable.
La máquina de Turing es capaz de hacer seis tipos
de operaciones fundamentales: leer, escribir,
mover hacia la izquierda, mover hacia la derecha,
cambiar de estado y detenerse.
Tiene la capacidad de computar cualquier cosa que
cualquier computadora moderna pueda calcular.

5. 01 02
03 04
TIPOS DE MAQUINA
DE TURING
Una máquina de Turing es un
dispositivo que transforma un
INPUT en un OUTPUT, ambos
formados por un código binario de
unos y ceros.
Máquinas de
Turing: con
movimiento stay
o “esperar”
Con cinta infinita
a ambos lados,
con cinta
multipista,
multicinta,
Determinista y no
determinista
Máquina de Turing
Cuántica

6. 6
El lenguaje de una Máquina de Turing
M=(Q,Σ,T,δ,q0,B,F)
es
L(M):={w∈Σ∗ : q0w⊢∗ αpβ,p∈F,α,β∈T∗}
Es decir, las w de Σ* tales que la máquina de
Turing alcanza un estado de aceptación.
01
Definición de la
Máquina de
Turing
03
Lenguaje de una
Máquina de Turing
02
La función de
transición
δ(q,X)=(p,Y,D)
M=(Q,Σ,T,δ,q0,B,F)
donde
•Q es el conjunto finito de estados que
denotaremos por: q0,q1,q2,...
•Σ es el alfabeto: el conjunto finito
de símbolos de entrada.
•Τ es el conjunto de símbolos de cinta. El
alfabeto es un subconjunto de Τ.
•q0 es el estado inicial: el estado en el que
se encuentra inicialmente la MT.
•B es un elemento de Σ: el símbolo en
blanco. Se encuentra en todas las casillas
de la cinta que no tienen un símbolo de
entrada.
•F es el conjunto de estados finales.
•δ es la función de transiciones.
MAQUINA DE TURING
indica que en el estado q, si la
cabeza de la MT señala al
símbolo de cinta X, entonces
la MT escribe el símbolo de
cinta Y en la casilla actual
(cambia X por Y ) y mueve la
cabeza una casilla
hacia D (D puede ser
derecha, R; o izquierda, L) y
pasa al estado p.

7. TEOREMAS
MAQUINA DE TURING
✋
030201 04 05
Sea L = L(M) el
lenguaje que
acepta una
máquina de
Turing no
determinista M,
entonces existe
una máquina de
Turing
determinista
N que acepta
dicho lenguaje, es
decir, L(M) =L (N).
Todo lenguaje
Recursivamente
Enumerable es
aceptado por
alguna máquina
de tres
contadores.
Todo lenguaje
aceptado por
una Máquina de
Turing de varias
cintas es
Recursivamente
Enumerable.
Sea L el
lenguaje
aceptado por
una máquina
de Turing,
entonces existe
algún
Autómata de
dos pilas que
acepta L.
Todo lenguaje
Recursivamente
Enumerable es
aceptado por
alguna máquina
de dos
contadores.
llamamos lenguaje
Recursivamente
Enumerable (RE) a
los lenguajes que
pueden ser
aceptados por una
Máquina de Turing.
Lenguaje
Recursivamente
Enumerable

8. Mueve el cabezal
a izquierda o
derecha
Escribe un
símbolo,
frente al
cabezal
Lee el símbolo,
frente al cabezal
4
3
2
1
Actualiza el
estado interno
CREANDO EL DIAGRAMA DE LA MT
MAQUINA DE TURING
Las máquinas de Turing pueden representarse
mediante grafos particulares, también
llamados diagramas de estados finitos

9. Una Máquina de Turing puede
representarse gráficamente a través de
los llamados Diagramas finitos o de
transición. Un diagrama de transición
está formado por un conjunto de nodos
que corresponden a los estados de la
MT. La transición δ(q,a)=(p,b,D) se
representa así:
OBTENIENDO EL DRAGRAMA
DE ESTADOS
MAQUINA DE TURING
👉
👉

10. 10
EJEMPLO
MAQUINA DE TURING
Diseñar una máquina de Turing que
acepta el lenguaje L={0n1n :n>0}
δ(q0,0)=(q1,X,R)δ(q0,0)=(q1,X,R)
δ(q1,0)=(q1,0,R)δ(q1,0)=(q1,0,R)
δ(q1,1)=(q2,Y,L)δ(q1,1)=(q2,Y,L)
δ(q2,0)=(q2,0,L)δ(q2,0)=(q2,0,L)
δ(q2,X)=(q0,X,R)δ(q2,X)=(q0,X,R)
δ(q1,Y)=(q3,Y,R)δ(q1,Y)=(q3,Y,R)
δ(q3,Y)=(q3,Y,R)δ(q3,Y)=(q3,Y,R)
δ(q3,1)=(q2,Y,L)δ(q3,1)=(q2,Y,L)
δ(q2,Y)=(q2,Y,L)δ(q2,Y)=(q2,Y,L)
δ(q0,Y)=(q0,Y,R)δ(q0,Y)=(q0,Y,R)
δ(q0,B)=(q4,B,R)δ(q0,B)=(q4,B,R)
La MT se quedará permanentemente en el
estado q1.
El diagrama de la MT es
El alfabeto: Σ={0,1} sólo puede aceptar palabras con de entrada
con símbolos 1 y 0.
Los símbolos de cinta serán T={0,1,B,X,Y} T={0,1,B,X,Y}
siendo B el símbolo en blanco.
La MT consta de cinco estados: q0,q1,q2,q3,q4
Los estados q0 y q4 son el inicial y el final, respectivamente.

11. REFERENCIAS
11
01 02
Feynman, Richard
(1996). Conferencias sobre
computación. ISBN 84-8432-444-3.
De Castro, Rodrigo
(2004). Teoría de la
computación : lenguajes,
autómatas, gramáticas
http://maquinasdeturing.blogspot
.com/2010_08_06_archive.html
https://ccc.inaoep.mx/~emorale
s/Cursos/Automatas/IntroMaqu
inasTuring.pdf