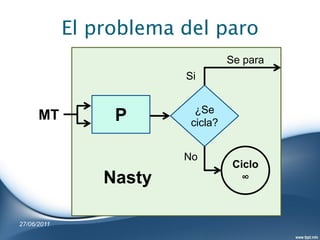
El documento aborda la Máquina de Turing y su relación con la computación y la inteligencia artificial, desarrollando antecedentes históricos y conceptos clave propuestos por Alan Turing y Alonzo Church. Se discute la tesis de Church-Turing, que establece que todo lo computable es Turing-computable, y se exploran implicaciones sobre la posibilidad de que el cerebro humano funcione como una computadora. Además, se presenta el problema del paro, que demuestra la existencia de problemas indecidibles, subrayando que no existe un algoritmo que determine si cualquier programa se detiene.

1. Máquina de Turing
M. C. Vicente Iván Sánchez Carmona
Ing. Diego Enrique Hernández González
Fac. de Ingeniería, UNAM
27/06/2011

2. Temario
 Antecedentes  ¿Y si el cerebro fuera
 Máquina de Turing una computadora?
 Componentes de la  Los peros
Máquina de Turing  El problema del paro
 Ejemplo  Si P fuera un ser
 Tesis de Church - humano
Turing  Sin embargo…
 Modelos  Bibliografía
equivalentes a la MT
27/06/2011

3. Antecedentes
 Durante los 30’s, Alan Turing, Alonzo Church,
entre otros, desarrollaron esquemas matemáticos
para poder especificar qué podía ser computado y
qué no.
 Kurt Gödel había demostrado que existen
problemas para los cuáles no hay solución lógica,
los cuales se denominan indecidibles
 El matemático Hilbert se preguntó si había un
método para poder determinar cuáles problemas
eran decidibles y cuáles no
27/06/2011

4. Antecedentes
 Para saber si un problema es decidible, este
debe ser resuelto por medio de un
procedimiento efectivo, esto es, un
algoritmo
 En 1936, Turing propuso un formalismo
lógico que representa el funcionamiento de
los algoritmos: una máquina abstracta
 Turing demostró que todo lo que un
humano puede computar, lo puede realizar
esta máquina
27/06/2011

5. Máquina de Turing
Es un mecanismo que consta de una
cinta de longitud infinita, y un cabezal
de lectura/escritura con el cual lee y
escribe símbolos sobre la cinta
27/06/2011

6. Componentes de la MT
 Un alfabeto de entrada (S)
 Un alfabeto de salida (G)
 Un conjunto de estados (Q) por los cuales
pasa durante su ejecución
 Una función de transición (d) que define
cómo es ejecutada la MT
 Un conjunto de estados finales (F) que
definen si la entrada de la MT es correcta o
no
27/06/2011

7. Ejemplo
MT que = 0 , 1
acepta una = 0
cadena con Σ = 0,1
un número
par de Γ = 0,1, ⊢,
ceros 0 , 0 = (1 , , )
0 , 1 = (0 , , )
=
1 , 0 = (0 , , )
27/06/2011
1 , 1 = (1 , , )

8. Tesis de Church - Turing
 Otro de los formalismos para demostrar qué
podía ser computable o no, el cálculo
lambda de Alonzo Church, fue encontrado
como equivalente a la máquina de Turing
 Todos los demás formalismos que fueron
desarrollados con este fin también se
encontraron como equivalentes a la MT
27/06/2011

9. Tesis de Church - Turing
Todo lo que es computable (lo que se
puede tomar en cuenta o evaluar) es
Turing-computable (existe una máquina
de Turing que lo puede realizar)
Todos los modelos que fueron desarrollados
posteriormente, y que al principio parecían
más poderosos, han sido reducidos a una
máquina de Turing, lo que lleva a pensar que
esta tesis es cierta
27/06/2011

10. Modelos equivalentes a la MT
 MT’s con más de una cinta
 MT’s con cintas de n dimensiones
 MT’s con un alfabetos ilimitados de
entrada y de salida
 El cálculo lambda
 Autómatas celulares
 Computadoras cuánticas
 Etcétera …
27/06/2011

11. ¿Y si el cerebro humano
fuera una computadora?
 Si fuera así, en principio, habría una
máquina de Turing equivalente al
cerebro
 Existiría un algoritmo que equivaldría
al funcionamiento de la mente
humana
 Por lo tanto, la Inteligencia Artificial es
factible
27/06/2011

12. Los peros
 Se piensa que en el cerebro hay
patrones que no pueden ser
representados matemáticamente, y en
consecuencia, no pueden ser
computados
 El cerebro humano puede saber si un
problema es indecidible o no
27/06/2011

13. El problema del paro
 Consiste en determinar si existe un
algoritmo (P) que pueda determinar si
otro algoritmo (MT) termina o en un
número finito de pasos, o en un bucle
infinito, ante cualquier entrada
MT Se para o
e
P se cicla
27/06/2011

14. El problema del paro
Se para
Si
¿Se
MT P cicla?
No
Ciclo
Nasty ∞
27/06/2011

15. Se para
Si
¿Se
P cicla?
No
Ciclo
Nasty ∞
27/06/2011

16. Problema del paro
 Si P dice que Nasty está parado, entonces
Nasty está un ciclo infinito
 Si P dice que Nasty está en un ciclo infinito,
entonces Nasty está parado
 En ambos casos, P está equivocado
 No existe ningún algoritmo P que pueda
determinar si cualquier programa se puede
detener o no ante cualquier entrada: este
caso no se puede determinar
27/06/2011

17. Si P fuera un ser humano
 Si P fuera un ser humano, sabría que
este caso (Nasty corriéndose a sí
mismo) es un problema indecidible
 Por lo tanto, un ser humano no puede
ser replicado por ningún algoritmo
27/06/2011

18. Sin embargo…
 Aún no se sabe si la máquina de
Turing es La definición de un
algoritmo, esto es sólo una tesis
 Si la computación no fuera capaz de
replicar la mente humana, nadie ha
demostrado tampoco que no exista
otra herramienta que si pueda hacerlo
27/06/2011

19. Bibliografía
 Hofstadter, D. Gödel, Escher, Bach: an
Eternal Golden Braid. 1979.
 Cohen, D. Introduction to Computer
Theory. Ed. Wiley & Sons.
27/06/2011